机器学习之聚类-2D数据类别划分

news2024/9/30 5:24:15

无监督学习（Unsupervised Learning）

机器学习的一种方法，没有给定事先标记过的训练示例，自动对输入的数据进行分类或分群。
image.png
方式一：站着或坐着
方式二：全身或半身
方式三：蓝眼球或不是蓝眼球

  • 没有对与错
  • 寻找数据的共同点

优点：

  • 算法不受监督信息（偏见）的约束，可能考虑到新的信息
  • 不需要标签数据，极大程度扩大数据样本

主要应用：聚类分析、关联规则、维度缩减
应用最广：聚类分析（clustering）

聚类分析

聚类分析又称为群分析，根据对象某些属性的相似度，将其自动化分为不同的类别

常用的聚类算法

KMeans聚类

  • 根据数据与中心点距离划分类别
  • 基于类别数据更新中心点
  • 重复过程直到收敛

特点

  • 实现简单，收敛快
  • 需要指定类别数量

均值漂移聚类（Meanshift）

  • 在中心点一定区域检索数据点
  • 更新中心
  • 重复流程到中心点稳定

特点

  • 自动发现类别数量，不需要人工选择
  • 需要选择区域半径

DBSCAN算法（基于密度的空间聚类算法）

  • 基于区域点密度筛选有效数据
  • 基于有效数据向周边扩张，直到没有新点加入

特点：

  • 过滤噪音数据
  • 不需要人为选择类别数量
  • 数据密度不同时影响结果

K均值聚类（KMeans Analysis）

以空间中k个点为中心进行聚类，对最靠近他们的对象归类，是聚类算法中最为基础但也最为重要的算法。
image.png
算法流程：

  1. 选择聚类的个数k
  2. 确定聚类中心
  3. 根据点到聚类中心聚类确定各个点所属类别
  4. 根据各个类别数据更新聚类中心
  5. 重复以上步骤直到收敛（中心点不再变化）

优点：

  1. 原理简单、实现容易、收敛速度快
  2. 参数少、方便使用

缺点：

  1. 必须设置簇的数量
  2. 随机选择初始聚类中心、结果可能缺乏一致性

原始数据分布
image.png
随机选取聚类中心
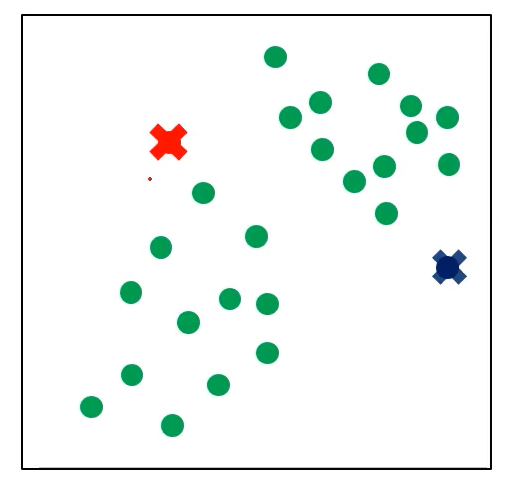
image.png
根据距离聚类
image.png
根据聚类更新中心
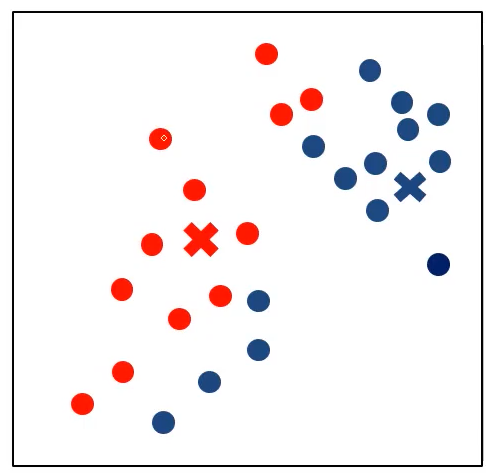
image.png
根据新的距离更新聚类
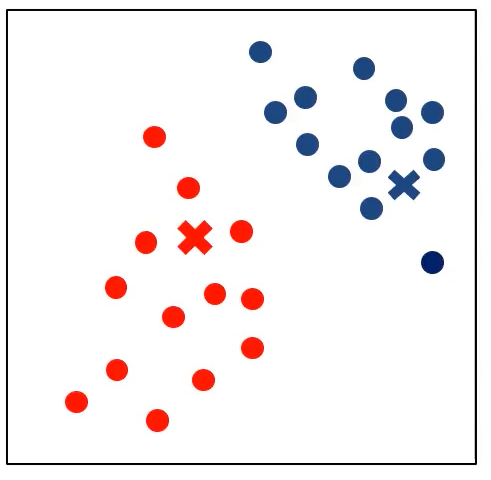
image.png
中心不再变化
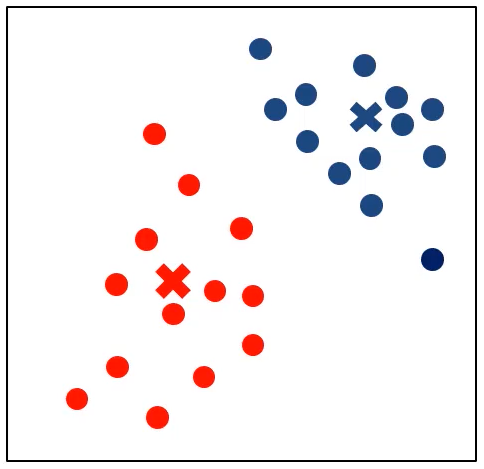
image.png

K近邻分类模型（KNN）

给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例（也就是上面所说的K个邻居），这K个实例的多数属于某个类，就把该输入实例分类到这个类中

  • 最简单的机器学习算法之一

image.png

均值漂移聚类

一种基于密度梯度上升的聚类算法（沿着密度上升方向寻找聚类中心点）
image.png
算法流程：

  1. 随机选择未分类点作为中心点
  2. 找出离中心点距离在带宽之内的点，记做集合S
  3. 计算从中心点到集合S中每个元素的偏移向量M
  4. 中心点以向量M移动
  5. 重复步骤2-4，直到收敛
  6. 重复1-5直到所有的点都被归类
  7. 分类：根据每个类，对每个点的访问频率，取访问频率最大的那个类，作为当前点集的所属类

实战准备

KMeans实现聚类
image.png
模型训练

from sklearn.cluster import KMeans
KM = KMeans(n_clusters=3,random_state=0)
KM.fit(X)

获取模型确定的中心点

centers = KM.cluster_centers_

准确率计算

from sklearn.metrics import accuuracy_score
accuracy = accuracy_score(y,y_predict)

结果矫正

y_cal=[]
for i in y_predict:
	if i==0:
    	y_cal.append(2)
    elif i == 1:
    	y_cal.append(1)
    else:
    	y_cal.append(0)
print(y_predict,y_cal)

Meanshift实现聚类

自动计算带宽（区域半径）

from sklearn.cluster import MeanShift,estimate_bandwidth
#detect bandwidth
bandwidth = estimate_bandwidth(X,n_samples=500)

模型建立与训练

ms = MeanShift(bandwidth=bandwidth)
ms.fit(X)

KNN实现分类

模型训练

from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X,y)

实战：2D数据类别划分

  1. 采用Kmeans算法实现2D数据自动聚类，预测V1=80,V2=60数据类别
  2. 计算预测准确率，完成结果矫正
  3. 采用KNN、Meanshift算法，重复步骤1-2

导入类加载数据

import pandas as pd
import numpy as np
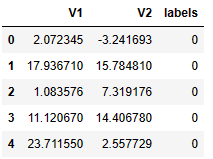
data=pd.read_csv('data.csv')
data.head()

image.png
数据初始化

X=data.drop(['labels'],axis=1)
y=data.loc[:,'labels']

查看个类别数量

pd.value_counts(y)

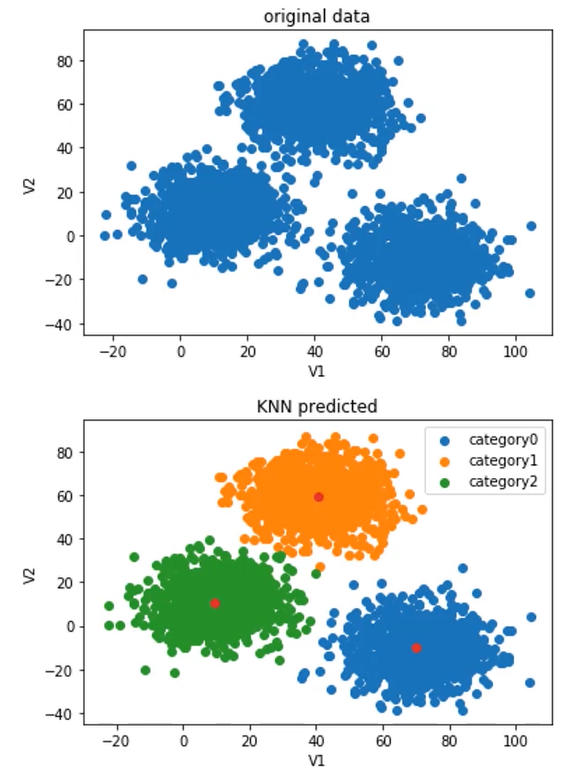
image.png
数据可视化

from matplotlib import pyplot as plt
fig1=plt.figure()
plt.scatter(X.loc[:,'V1'],X.loc[:,'V2'])
plt.title("un-labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.show()

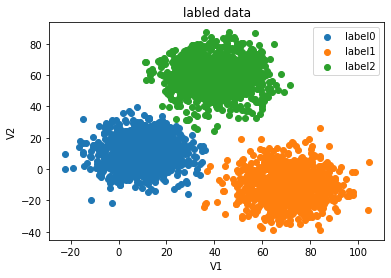
image.png

fig1=plt.figure()
label0=plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
label1=plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
label2=plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

image.png
模型训练

from sklearn.cluster import KMeans
KM = KMeans(n_clusters=3,random_state=0)
KM.fit(X)

查看聚类的中心点

KM.cluster_centers_

image.png
可视化中心点

centers = KM.cluster_centers_
fig3=plt.figure()
plt.scatter(centers[:,0],centers[:,1])
plt.show()

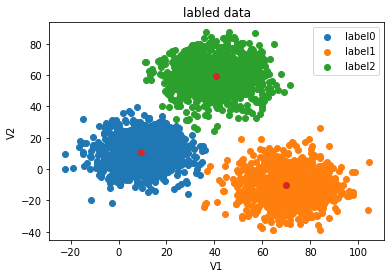
image.png

centers = KM.cluster_centers_
fig3=plt.figure()
label0=plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
label1=plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
label2=plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

image.png
模型评估

y_predict_test = KM.predict([[80,60]])
y_predict=KM.predict(X)
print(pd.value_counts(y_predict),pd.value_counts(y))
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

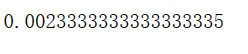
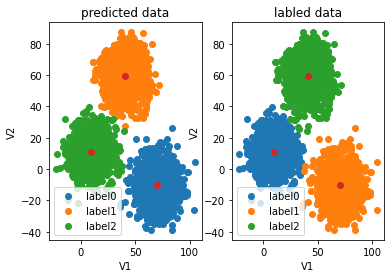
image.png

fig4=plt.subplot(121)
label0=plt.scatter(X.loc[:,'V1'][y_predict==0],X.loc[:,'V2'][y_predict==0])
label1=plt.scatter(X.loc[:,'V1'][y_predict==1],X.loc[:,'V2'][y_predict==1])
label2=plt.scatter(X.loc[:,'V1'][y_predict==2],X.loc[:,'V2'][y_predict==2])
plt.title("predicted data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))

fig4=plt.subplot(122)
label0=plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
label1=plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
label2=plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

image.png
模型矫正

y_corrected=[]
for i in y_predict:
    if i==0:
        y_corrected.append(1)
    elif i==1:
        y_corrected.append(2)
    else:
        y_corrected.append(0)
print(pd.value_counts(y_corrected))
print(pd.value_counts(y))

image.png
模块评估

print(accuracy_score(y,y_corrected))

image.png
可视化

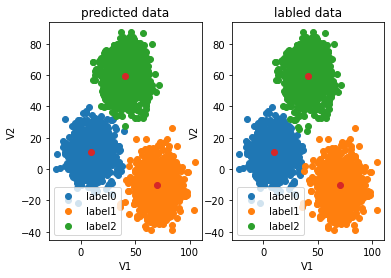
fig4=plt.subplot(121)
label0=plt.scatter(X.loc[:,'V1'][y_corrected==0],X.loc[:,'V2'][y_corrected==0])
label1=plt.scatter(X.loc[:,'V1'][y_corrected==1],X.loc[:,'V2'][y_corrected==1])
label2=plt.scatter(X.loc[:,'V1'][y_corrected==2],X.loc[:,'V2'][y_corrected==2])
plt.title("corrected data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))

fig4=plt.subplot(122)
label0=plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
label1=plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
label2=plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

image.png

KNN

模型训练

from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X,y)

显示预测结果 评估模型

y_predict_knn_test=KNN.predict([[80,60]])
y_predict_knn=KNN.predict(X)
print(y_predict_knn_test)
print('knn accuracy',accuracy_score(y,y_predict_knn))

image.png
查看模型分布

print(pd.value_counts(y_predict_knn))
print(pd.value_counts(y))

image.png
可视化

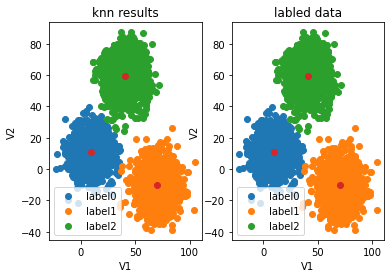
fig5=plt.subplot(121)
label0=plt.scatter(X.loc[:,'V1'][y_predict_knn==0],X.loc[:,'V2'][y_predict_knn==0])
label1=plt.scatter(X.loc[:,'V1'][y_predict_knn==1],X.loc[:,'V2'][y_predict_knn==1])
label2=plt.scatter(X.loc[:,'V1'][y_predict_knn==2],X.loc[:,'V2'][y_predict_knn==2])
plt.title("knn results")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))

fig6=plt.subplot(122)
label0=plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
label1=plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
label2=plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

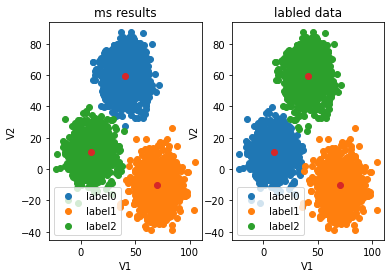
image.png

meanshift

from sklearn.cluster import MeanShift,estimate_bandwidth
bw = estimate_bandwidth(X,n_samples=500)

模型训练

ms=MeanShift(bandwidth=bw)
ms.fit(X)

查看预测结果

y_predict_ms = ms.predict(X)
print(pd.value_counts(y_predict_ms))
print(pd.value_counts(y))

image.png
可视化

fig5=plt.subplot(121)
label0=plt.scatter(X.loc[:,'V1'][y_predict_ms==0],X.loc[:,'V2'][y_predict_ms==0])
label1=plt.scatter(X.loc[:,'V1'][y_predict_ms==1],X.loc[:,'V2'][y_predict_ms==1])
label2=plt.scatter(X.loc[:,'V1'][y_predict_ms==2],X.loc[:,'V2'][y_predict_ms==2])
plt.title("ms results")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))

fig6=plt.subplot(122)
label0=plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
label1=plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
label2=plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

image.png
模型矫正

y_corrected_ms=[]
for i in y_predict_ms:
    if i==0:
        y_corrected_ms.append(2)
    elif i==1:
        y_corrected_ms.append(1)
    else:
        y_corrected_ms.append(0)
print(pd.value_counts(y_corrected_ms))
print(pd.value_counts(y))

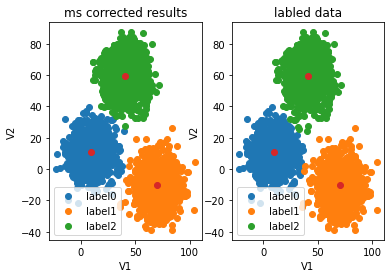
image.png
可视化

y_corrected_ms = np.array(y_corrected_ms)
fig5=plt.subplot(121)
label0=plt.scatter(X.loc[:,'V1'][y_corrected_ms==0],X.loc[:,'V2'][y_corrected_ms==0])
label1=plt.scatter(X.loc[:,'V1'][y_corrected_ms==1],X.loc[:,'V2'][y_corrected_ms==1])
label2=plt.scatter(X.loc[:,'V1'][y_corrected_ms==2],X.loc[:,'V2'][y_corrected_ms==2])
plt.title("ms corrected results")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))

fig6=plt.subplot(122)
label0=plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
label1=plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
label2=plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.scatter(centers[:,0],centers[:,1])
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

image.png

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1407295.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

解决TortoiseGit软件Git Show log时显示Too many files to display的问题

解决TortoiseGit软件Git Show log时显示Too many files to display的问题

1 问题描述 有时代码提交修改的文件比较多，当查看log时无法显示出来修改的文件列表，如下所示： 2 解决方法 将LogTooManyItemsThreshold尽可能配置得大一些。 三 参考资料 https://gitlab.com/tortoisegit/tortoisegit/-/issues/3878
阅读更多...
使用 Docker 部署 ServerStatus 服务器监控系统

使用 Docker 部署 ServerStatus 服务器监控系统

一、ServerStatus 介绍 GitHub：https://github.com/cppla/ServerStatus ServerStatus 是一个酷炫高逼格的云探针、云监控、服务器云监控、多服务器探针~。 特性 使用 Rust 完全重写 Server、Client，单个执行文件部署支持上下线和简单自定义规则告警 (T…
阅读更多...
01. eNSP环境以及VRP基本使用

01. eNSP环境以及VRP基本使用

eNSP的基本使用 1. eNSP的桥连接1.1. 具体操作（1）创建环回适配器（2）设置虚拟网卡（3）使用eNSP桥接计算机 2. 华为VRP系统2.1. 实验1：VRP的基本操作2.2. 实验2：文件命令（1&…
阅读更多...
mysql 基础（三）

mysql 基础（三）

一、多表设计 数据库设计范式 第一范式(确保每列保持原子性) 第一范式是最基本的范式。如果数据库表中的所有字段值都是不可分解的原子值，就说明该数据库表满足了第一范式。第二范式就是要有主键，要求其他字段都依赖于主键。 没有主键就没有唯一性&…
阅读更多...
el-tree勾选后退出再打开显示之前已经勾选的

el-tree勾选后退出再打开显示之前已经勾选的

官网文档 element-ui官网文档有默认展开和默认选中 <el-tree:data"data"show-checkboxnode-key"id":default-expanded-keys"[2, 3]":default-checked-keys"[5]":props"defaultProps"> </el-tree><script>…
阅读更多...
力扣518. 零钱兑换 II

力扣518. 零钱兑换 II

动态规划 思路&#xff1a; 假设 dp[i] 为金额 i 使用零钱的组合数&#xff0c;其可以由其中的一种零钱 coin 和 i - coin 组合&#xff1b; 遍历零钱数组&#xff0c;对每一种零钱 coin 进行如下操作&#xff1a; 从 coin 到 amount 金额进行遍历&#xff0c;dp[j] dp[j] d…
阅读更多...
Prometheus 薪资翻倍的监控系统？

Prometheus 薪资翻倍的监控系统？

1. 介绍与架构 Prometheus是一个开源的系统监控和警报工具包&#xff0c;用于收集和存储时间序列数据&#xff0c;包括指标信息、记录时间戳以及可选的键值对标签。许多公司使用Prometheus监控K8s集群。 2. 合适与不合适场景 合适场景 Prometheus适用于记录各种数字时间序列…
阅读更多...
web系统架构基于springCloud的各技术栈

web系统架构基于springCloud的各技术栈

博主目前开发的web系统架构是基于springCloud的一套微服务架构。 使用的技术栈&#xff1a;springbootmysqlclickhousepostgresqlredisrocketMqosseurekabase-gatewayapollodockernginxvue的一套web架构。 一、springboot3.0 特性&#xff1a;Spring Boot 3.0提供了许多新特性…
阅读更多...
每日一题——LeetCode1313.解压缩编码列表

每日一题——LeetCode1313.解压缩编码列表

这么简单的题目要说的这么复杂 nums里每相邻的两个元素nums[i]、nums[j]为一对&#xff0c;nums[i]表示nums[j]的次数 var decompressRLElist function(nums) {let res[]for(let i0,j1;j<nums.length-1;i2,j2){while(nums[i]--){res.push(nums[j])}}return res }; 消耗时…
阅读更多...
代码随想录 Leetcode107. 二叉树的层序遍历 II

代码随想录 Leetcode107. 二叉树的层序遍历 II

题目&#xff1a; 代码&#xff08;首刷自解 2024年1月24日&#xff09;&#xff1a; class Solution { public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> res {};if(root nullptr) return res;queue<TreeNode…
阅读更多...
第11次修改了可删除可持久保存的前端html备忘录：将样式分离，可以自由秒添加秒删除样式

第11次修改了可删除可持久保存的前端html备忘录：将样式分离，可以自由秒添加秒删除样式

第11次修改了可删除可持久保存的前端html备忘录&#xff1a;将样式分离&#xff0c;可以自由秒添加秒删除样式 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"…
阅读更多...
Cesium for Unity包无法加载

Cesium for Unity包无法加载

太上老君急急如律⚡令⚡ &#x1f959;关闭UnityHub&#x1f9c0;启动梯子&#x1f96a;cmd 启动UnityHub &#x1f959;关闭UnityHub &#x1f9c0;启动梯子 &#x1f96a;cmd 启动UnityHub 把批处理启动文件&#x1f448;中的exe的路径换成自己的安装目录&#xff01;保存…
阅读更多...
使用Electron打包vue文件变成exe应用程序

使用Electron打包vue文件变成exe应用程序

文章目录 一、下载Electron二、修改下载的Electron项目1.修改index.html文件2.修改main.js文件3.修改package.json文件 三、修改vue项目1.修改vite.config.js文件2.修改.env.production文件3.修改auth.js文件4.修改router下得index.js文件6.修改Navbar.vue文件 四、Electron打包…
阅读更多...
ARMv8-AArch64 的异常处理模型详解之异常类型 Exception types

ARMv8-AArch64 的异常处理模型详解之异常类型 Exception types

异常类型详解 Exception types 一&#xff0c; 什么是异常二&#xff0c;同步异常&#xff08;synchronous exceptions&#xff09;2.1 无效的指令和陷阱异常&#xff08;Invalid instructions and trap exceptions&#xff09;2.2 内存访问产生的异常2.3 产生异常的指令2.4 调…
阅读更多...
Type-c一分二C+L/C+C同时快充数据线方案

Type-c一分二C+L/C+C同时快充数据线方案

一分二快充线是一种具有同时快充功能的线缆&#xff0c;可以实现同时给两个设备充电&#xff0c;并且都能达到快充的效果。那么&#xff0c;一分二快充线是如何实现同时快充功能的呢&#xff1f; 首先&#xff0c;一分二快充线采用了一种高效能的充电芯片LDR6020&#xff0c;这…
阅读更多...
文件上传技术总结

文件上传技术总结

语言可解析的后缀 &#xff08;前提&#xff1a;在Apache httpd.conf 配置文件中有特殊语言的配置 AddHandler application/x-httpd-php .php 搭配大小写、双重、空格来进行 其中&#xff1a; phtml、pht、php3、php4和php5都是Apache和php认可的php程序的文件后缀 常见的…
阅读更多...
Web开发4：单元测试

Web开发4：单元测试

在Web开发中&#xff0c;单元测试是一种重要的开发实践&#xff0c;它可以帮助我们确保代码的质量和可靠性。通过编写和运行单元测试&#xff0c;我们可以验证代码的正确性&#xff0c;减少错误和缺陷&#xff0c;并提高代码的可维护性。本文将介绍单元测试的概念、好处以及如何…
阅读更多...
Markdown 数学公式详细总结

Markdown 数学公式详细总结

✍️作者简介&#xff1a;小北编程&#xff08;专注于HarmonyOS、Android、Java、Web、TCP/IP等技术方向&#xff09; &#x1f433;博客主页&#xff1a;开源中国、稀土掘金、51cto博客、博客园、知乎、简书、慕课网、CSDN &#x1f514;如果文章对您有一定的帮助请&#x1f4…
阅读更多...
二分搜索树(Java）

二分搜索树(Java）

完整代码在最后 树结构&#xff1a; 1.树结构本身是一种天然的组织结构 2.高效 二分搜索树的基础 1、二叉树 1.和链表一样&#xff1a;动态存储 2.具有唯一的根 3.每个结点最多只有2个孩子&#xff0c;每个结点最多只有一个父亲 4.具有天然的递归结构 2、满二叉树 a. 叶子…
阅读更多...
关于IP地址欺骗的知识，看这篇文章就差不多了

关于IP地址欺骗的知识，看这篇文章就差不多了

无论是什么媒介，身份盗窃始终是一种威胁。所谓的“IP欺骗”是恶意用户为了他们的黑客攻击企图快速获得可信度的一种常见方式。 考虑到每台计算机和服务器都有一个唯一的标识符（Internet Protocol或IP地址），几乎任何使用互联网的人都可能受到攻击。IP欺骗是一种“伪造”源地…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023