acwing 动态规划dp 0 1背包问题

前言

hello小伙伴们，最近由于个人放假原因颓废了一段时间很长时间没有更新CSDN的内容了，唉，毕竟懂得都懂寒暑假静下心来学习的难度远比在学校里大的多。

但是，也不是毫无办法克服，今天我来了我们当地的一家自习室来学习，感觉效果比在家强很多，趁机写一下博客分享一下最近的收获。

今天没写蓝桥杯备赛系列因为我感觉这块内容应该是蓝桥杯的一个重点考察方向，所以我想先讲知识点然后过渡讲蓝桥杯系列，包括dfs、bfs那块内容也是这个套路，尽量是能让我和大家收获最大为好。不多bb上内容。

DP 01背包模型

DP（动态规划）内容核心讲解

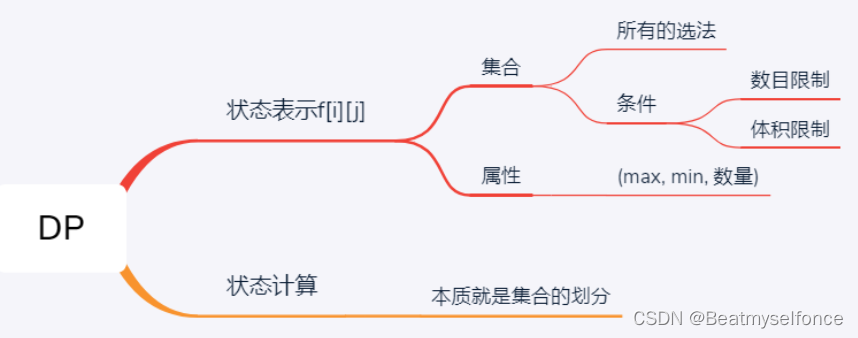
状态表示：用一个数组f[][](数组可能是一维也可能是二维，根据具体题目具体分析）来表示某个集合，这个集合表示所有的做法，集合存的值就是对应做法的属性（一般是max，min，count）（换句话说：f[i][j]表示在限制i,j下做法的属性）
状态转移：本质上是一个优化的过程，就是不断更新状态。

01背包问题

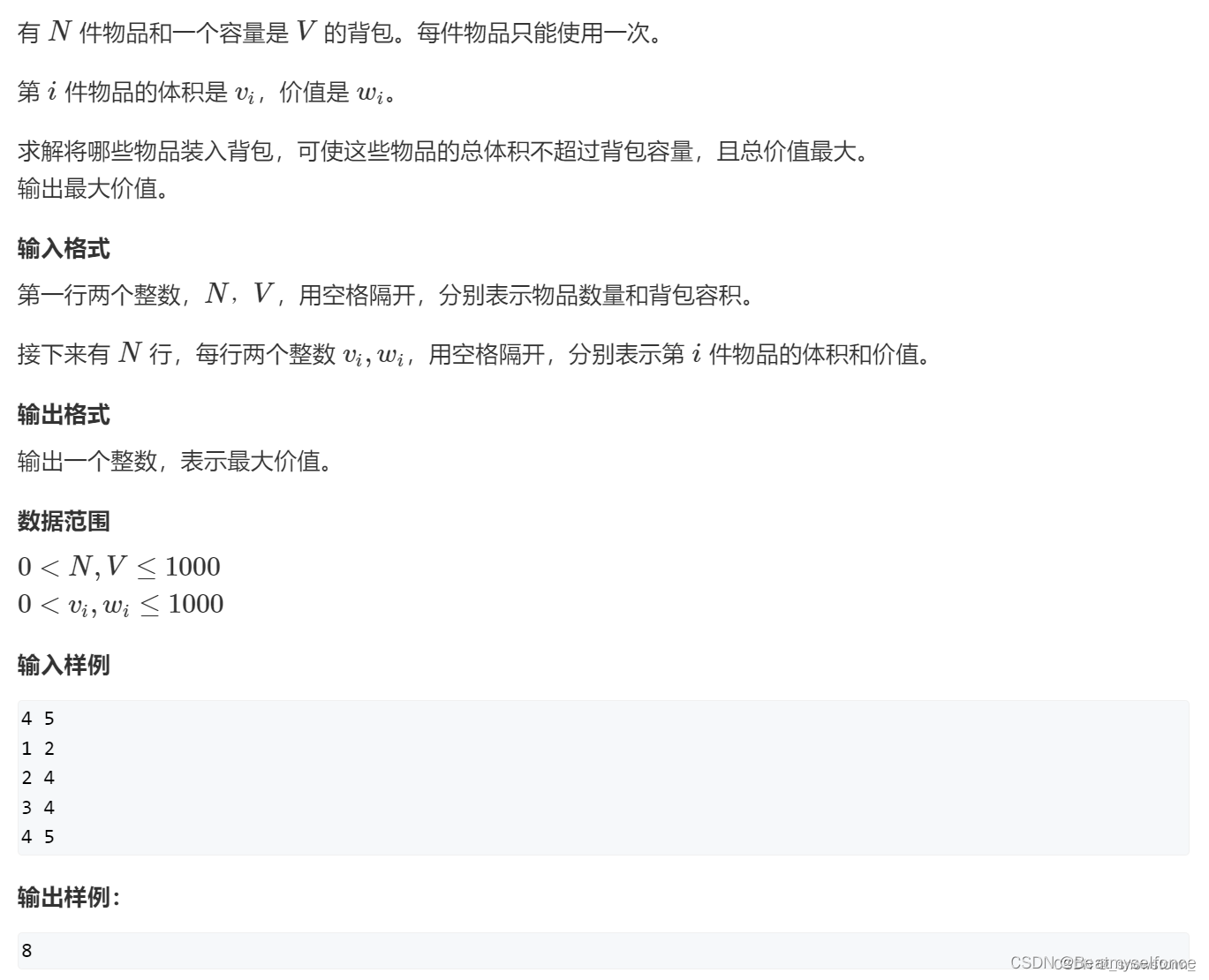
思路

重要变量说明：

f[][]:用于状态表示；

w[]:记录每个物品的价值

v[]:记录每个物品的体积

1. 定义二维数组f[][],其中f[i][j]表示在前i个物品，背包容积为j的限制下所能装下的最大价值。这里的f[i][j]就是做法的集合，f[i][j]的值就是最大价值即属性。
2. 从i=1开始枚举，对于第i个物品，都有选和不选两种选择：
如果不选第i个物品，那么状态转移方程为f[i][j]=f[i-1][j]
如果选择第i个物品，那么状态转移方程为f[i][j]=f[i-1][j-v[i]]+w[i]
3. 我们因为要求最大价值，所以对上面两种情况去max即可

为什么可以转为一维

首先观察状态转移方程 dp[i][j]是由 dp[i-1][jxxxx]推导而来，仅看第一个维度，即i - 1 与 i ，可以发现第i层是由上一层推导而来的。

故我们不必要保存i - 2 层，比如我们计算第三层是只需要第二层的。不需要第一层的数据。

当我们去掉i时，即我们不需要控制第几层，只需要长度为j的数组，保存确认过最新的一层。作为下一层的参考。例如我们计算第三层dp时，此时dp原数据保存的是第二层的结果。

为什么要逆序

首先，通过上一个问题，我们确认了我们目前一维的dp数组，保存的是确认过的最新一层的数据，即上一层的数据。

当我们计算当前层时，对于二维时的状态转移方程有

dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);

可以看到，dp[i - 1][j - v[i]] + w[i] 使用的上一层的原始数据（dp[i - 1]），而我们使用一维的状态转移方程时有

dp[j] = max(dp[j], dp[j - v[i]] + w[i]);

当我们从小到大更新是，因为j - v[i] 是严格小于j 的，所以我们可以举个例子 dp[3] = max(dp[3], dp[2] + 1); 因为我们是从小到大更新的，所以当更新到dp[3]的时候，dp[2]已经更新过了，已经不是上一层的dp[2]。

而当我们逆序更新时有，举例 dp[8] = max(dp[8], dp[6] + 2)当更新dp[8]时，dp[6]还没有被更新，还是上一层的数据，这样才能保证没有读入脏数据。

#include<iostream>

using namespace std;
const int N=1010;
int f[N][N],v[N],w[N];

int main()
{
    int n,V;
    cin>>n>>V;
    for(int i=1;i<=n;i++)   
        cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)       //从第一个物品开始选，直到最后一个物品结束
        for(int j=1;j<=V;j++)       //从最小的体积开始，直到背包的最大的容积
        {
            if(j-v[i]>=0)       //可以装第i个物品
                f[i][j]=f[i-1][j-v[i]]+w[i];        //状态转移
            f[i][j]=max(f[i][j],f[i-1][j]);     //状态转移，两种情况取最大值
        }
    cout<<f[n][V]<<endl;
    return 0;
}

优化1（滚动数组）

注意： 这里优化的的是空间而不是时间

思路

我们注意到其实上面写的f[i][j]其实每次计算只是用到了第i层和第i-1层，所以我们数组的第一维其实只用开两个即可。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int v[N];
int w[N];
int f[N][N];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i ++) scanf("%d%d",&v[i],&w[i]);
    for(int i = 1;i <= n;i ++){
        for(int j = 0;j <= m;j ++){
            f[i % 2][j] = f[(i - 1) % 2][j];
            if(j >= v[i]) f[i % 2][j] = max(f[i % 2][j],f[(i - 1) % 2][j - v[i]] + w[i]);
        }
    }
    printf("%d",f[n % 2][m]);
    return 0;
}

优化2（一维数组）

我们可以把二维数组优化到一维数组
为什么可以这样变形呢？我们定义的状态f[i][j]可以求得任意合法的i与j最优解，但题目只需要求得最终状态f[n][m]，因此我们只需要一维的空间来更新状态

思路

定义f[]表示状态，f[j]表示在N个物品，背包容积为j下所能装下的最大价值。
也还是从i开始枚举，表示选与不选第i个物品。
注意
我们要逆序枚举背包容积，即每次循环从背包的最大容积开始枚举。
**原因如下：**在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
**简单来说：**简单来说，一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」，逆序则不会有这样的问题。

来个例子

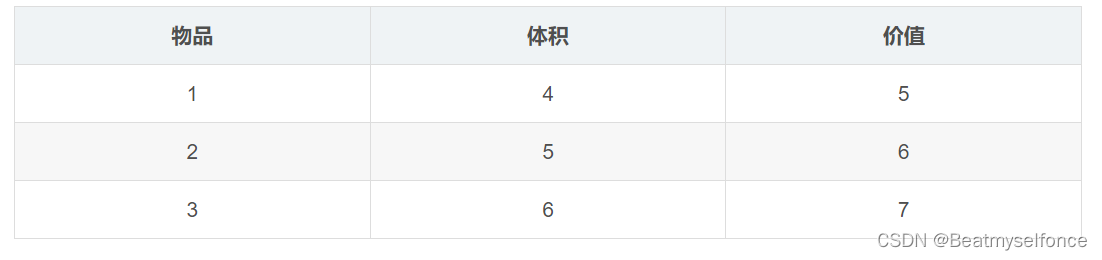
如果 j 层循环是递增的：
for (int i = 1; i <= n; i++) {
for (int j = v[i]; j <= m; j++) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}

经典代数法模拟运行过程

    当还未进入循环时:
    f[0] = 0;  f[1] = 0;  f[2] = 0;  f[3] = 0;  f[4] = 0;  
    f[5] = 0;  f[6] = 0;  f[7] = 0;  f[8] = 0;  f[9] = 0; f[10] = 0;
    当进入循环 i == 1 时：
    f[4] = max(f[4], f[0] + 5); 即max(0, 5) = 5; 即f[4] = 5;
    f[5] = max(f[5], f[1] + 5); 即max(0, 5) = 5; 即f[5] = 5;
    f[6] = max(f[6], f[2] + 5); 即max(0, 5) = 5; 即f[6] = 5;
    f[7] = max(f[7], f[3] + 5); 即max(0, 5) = 5; 即f[7] = 5;
    重点来了！！！
    f[8] = max(f[8], f[4] + 5); 即max(0, 5 + 5) = 10; 即f[8] = 10;
    这里就已经出错了
    因为此时处于 i == 1 这一层，即物品只有一件，不存在单件物品满足价值为10
    所以已经出错了。

如果 j 层循环是逆序的：
for (int i = 1; i <= n; i++) {
for (int j = m; j >= v[i]; j--) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}

代数法模拟过程

    当还未进入循环时:
    f[0] = 0;  f[1] = 0;  f[2] = 0;  f[3] = 0;  f[4] = 0;  
    f[5] = 0;  f[6] = 0;  f[7] = 0;  f[8] = 0;  f[9] = 0; f[10] = 0;
    当进入循环 i == 1 时：w[i] = 5; v[i] = 4;
    j = 10：f[10] = max(f[10], f[6] + 5); 即max(0, 5) = 5; 即f[10] = 5;
    j = 9 ：f[9] = max(f[9], f[5] + 5); 即max(0, 5) = 5; 即f[9] = 5;
    j = 8 ：f[8] = max(f[8], f[4] + 5); 即max(0, 5) = 5; 即f[8] = 5;
    j = 7 ：f[7] = max(f[7], f[3] + 5); 即max(0, 5) = 5; 即f[7] = 5;
    j = 6 ：f[6] = max(f[6], f[2] + 5); 即max(0, 5) = 5; 即f[6] = 5;
    j = 5 ：f[5] = max(f[5], f[1] + 5); 即max(0, 5) = 5; 即f[5] = 5;
    j = 4 ：f[6] = max(f[4], f[0] + 5); 即max(0, 5) = 5; 即f[4] = 5;
    当进入循环 i == 2 时：w[i] = 6; v[i] = 5; 
    j = 10：f[10] = max(f[10], f[5] + 6); 即max(5, 11) = 11; 即f[10] = 11;
    j = 9 ：f[9] = max(f[9], f[4] + 6); 即max(5, 11) = 5; 即f[9] = 11;
    j = 8 ：f[8] = max(f[8], f[3] + 6); 即max(5, 6) = 6; 即f[8] = 6;
    j = 7 ：f[7] = max(f[7], f[2] + 6); 即max(5, 6) = 6; 即f[7] = 6;
    j = 6 ：f[6] = max(f[6], f[1] + 6); 即max(5, 6) = 6; 即f[6] = 6;
    j = 5 ：f[5] = max(f[5], f[0] + 6); 即max(5, 6) = 6; 即f[5] = 6;
    当进入循环 i == 3 时: w[i] = 7; v[i] = 6; 
    j = 10：f[10] = max(f[10], f[4] + 7); 即max(11, 12) = 12; 即f[10] = 12;
    j = 9 ：f[9] = max(f[9], f[3] + 6); 即max(11, 6) = 11; 即f[9] = 11;
    j = 8 ：f[8] = max(f[8], f[2] + 6); 即max(6, 6) = 6; 即f[8] = 6;
    j = 7 ：f[7] = max(f[7], f[1] + 6); 即max(6, 6) = 6; 即f[7] = 6;
    j = 6 ：f[6] = max(f[6], f[0] + 6); 即max(6, 6) = 6; 即f[6] = 6;

一维代码优化后

#include<iostream>

using namespace std;
const int N=1010;
int f[N],v[N],w[N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
        for(int j=m;j>=v[i];j--)        //逆序，防止被数据污染
            f[j]=max(f[j],f[j-v[i]]+w[i]);
    cout<<f[m]<<endl;
    return 0;
}

今天就讲完了全部内容，但是我从如下几个方面总结一下今天讲的内容

首先讲了dp问题的大思路，然后给大家放了一下acwing上面的那个例题，然后给大家讲解了一下为什么二维可以转一维。

下次讲全部背包问题，讲完dp问题上蓝桥杯习题课系列，到时候就不讲知识点了。