雅可比矩阵的第Ji列:
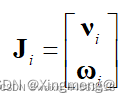
关于一些基本概念可以参考博客,部分细节如下:
每个移动关节,Ji可以这样计算:

每个旋转关节,Ji这样计算:

有时候要求按照末端执行器坐标系{n}来执行一些位移旋转之类的操作,在末端执行器坐标系下的雅可比矩阵可以这样计算:

SDH代码程序参考博客,如下:
function [ J ] = Jacob_cross_SDH( q )
%JACOB_CROSS_SDH 函数摘要
% 输入q0为逼近角,单位为弧度,矩阵大小1*6;
% 输出J为速度雅各比矩阵,矩阵大小6*6;
% 说明:利用向量积的方法求解系统的雅各比矩阵,方法1和方法2任选一种
% 说明:此求解方法基于SDH参数建模,若MDH方法建模,需进行一定的下标改动
d=[105.03,0,0,75.66,80.09,44.36];
a=[0,-174.42,-174.42,0,0,0];
alp=[pi/2,0,0,pi/2,-pi/2,0];
offset=[0,-pi/2,0,-pi/2,0,0];
thd=q+offset;
% 求各个关节间的变换矩阵
T0=trotz(0)*transl(0,0,0)*trotx(0)*transl(0,0,0);
T1=trotz(thd(1))*transl(0,0,d(1))*trotx(alp(1))*transl(a(1),0,0);
T2=trotz(thd(2))*transl(0,0,d(2))*trotx(alp(2))*transl(a(2),0,0);
T3=trotz(thd(3))*transl(0,0,d(3))*trotx(alp(3))*transl(a(3),0,0);
T4=trotz(thd(4))*transl(0,0,d(4))*trotx(alp(4))*transl(a(4),0,0);
T5=trotz(thd(5))*transl(0,0,d(5))*trotx(alp(5))*transl(a(5),0,0);
T6=trotz(thd(6))*transl(0,0,d(6))*trotx(alp(6))*transl(a(6),0,0);
% 求各个关节相对于惯性坐标系的变换矩阵
T00 = T0;
T01 = T1;
T02 = T1*T2;
T03 = T1*T2*T3;
T04 = T1*T2*T3*T4;
T05 = T1*T2*T3*T4*T5;
T06 = T1*T2*T3*T4*T5*T6;
% 求各个关节相对于末端坐标系的变换矩阵
T06 = T1*T2*T3*T4*T5*T6;
T16 = T2*T3*T4*T5*T6;
T26 = T3*T4*T5*T6;
T36 = T4*T5*T6;
T46 = T5*T6;
T56 = T6;
% 提取各变换矩阵的旋转矩阵
R00 = t2r(T00);
R01 = t2r(T01);
R02 = t2r(T02);
R03 = t2r(T03);
R04 = t2r(T04);
R05 = t2r(T05);
R06 = t2r(T06);
% 取旋转矩阵第3列,即Z轴方向分量
Z0 = R00(: , 3);
Z1 = R01(: , 3);
Z2 = R02(: , 3);
Z3 = R03(: , 3);
Z4 = R04(: , 3);
Z5 = R05(: , 3);
Z6 = R06(: , 3);
%% Method.1
% 求末端关节坐标系相对于前面各个坐标系的位置,即齐次变换矩阵的第四列
% pi6为坐标系i和末端坐标系的相对位置在坐标系i下的表示
P06 = T06(1:3, 4);
P16 = T16(1:3, 4);
P26 = T26(1:3, 4);
P36 = T36(1:3, 4);
P46 = T46(1:3, 4);
P56 = T56(1:3, 4);
P66 = [0; 0; 0];
% 使用向量积求出雅可比矩阵
% R0i为坐标系0到坐标系i的旋转矩阵
% R0i*Pi6指坐标系i和末端坐标系的相对位置在0坐标系下的表示
J1 = [cross(Z0, R00*P06); Z0];
J2 = [cross(Z1, R01*P16); Z1];
J3 = [cross(Z2, R02*P26); Z2];
J4 = [cross(Z3, R03*P36); Z3];
J5 = [cross(Z4, R04*P46); Z4];
J6 = [cross(Z5, R05*P56); Z5];
%% Method.2
% % pi为坐标系i与世界坐标系0的相对位置
% p0=transl(T00);
% p1=transl(T01);
% p2=transl(T02);
% p3=transl(T03);
% p4=transl(T04);
% p5=transl(T05);
% p6=transl(T06);
%
% % p6-pi为i坐标系指向末端坐标系的向量
% % p6-pi即为末端坐标系与i坐标系相对位置在世界坐标系中的表示
% % Ji=[Jv;Jw] 对应六自由度的速度分量和旋转分量
% J1 = [cross(Z0, p6-p0); Z0];
% J2 = [cross(Z1, p6-p1); Z1];
% J3 = [cross(Z2, p6-p2); Z2];
% J4 = [cross(Z3, p6-p3); Z3];
% J5 = [cross(Z4, p6-p4); Z4];
% J6 = [cross(Z5, p6-p5); Z5];
J = [J1, J2, J3, J4, J5, J6];
end
![[Linux]HTTP状态响应码列举](https://img-blog.csdnimg.cn/direct/836e694c716c4b6baddadb7099dbbeed.jpeg#pic_center)