文章目录
- 题目
- 代码
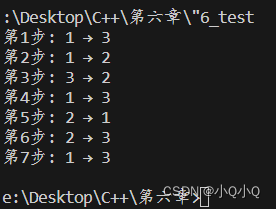
- 运行截图
题目
(汉诺塔问题)在这一章中大家了解了既可以用递归方法又可以用迭代方法很容易实现的函数。不过,在这道练习题中,我们提出的问题若用递归来解决,则尽显递归之优雅:若用迭代来实现,恐怕没那么容易。
汉诺塔问题是每个新一代的计算机科学家必须掌握的最著名的经典问题之一。传说在遥远的东方有一座庙,僧侣们尝试把一叠金盘从一根木桩上移到另一根木上(如图6.34 所示)。起初有64个金盘串在一个木桩上,从下到上尺寸逐步缩小。僧侣们尝试着按照一次只能移动一个金盘并目大的金盘永远不能放在小的金盘上面的规定,将这叠金盘移动到另外一个木桩上。总共有三个木桩,一个用于暂放金盘。按照推测,僧侣们完成他们的工作之时,正是地球毁灭之日。若真是这样,我们可不愿意助他们一臂之力了。
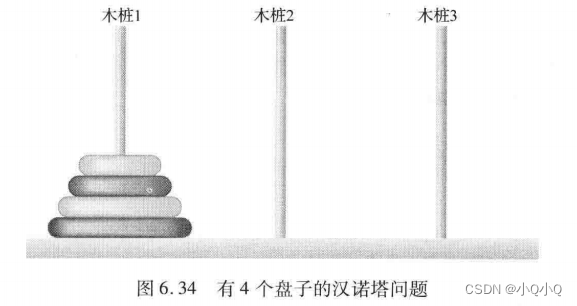
假设僧侣们想把盘子从木桩1移到木3。我们希望开发一个算法,显示僧侣从木桩到木桩移动盘子的序列。
如果使用传统的方法来处理这个问题,会很快发现我们陷人到这堆盘子的管理之中而无法自拔这个问题很棘手,似乎没有什么希望解决它。然而,用递归的方法来处理这个问题,解决思路就很简单。移动n个盘子问题可以看成如下所示的移动n-1个盘子的问题(因此是递归问题):
a)把n-1个盘子从木桩1移到木桩2把木3作为临时存放点
b)把最后一个盘子(最大的)从木桩1移到木3。
c)把n-1个盘子从木桩2移到木3把1作为临时存放点。
当最后一次任务只有n=1个盘子要移动时(即基本情况),整个过程就结束了。这时只需要轻松地把盘子移过去就可以了,不再需要临时存放点。请编写一个程序解决汉诺塔问题。其中利用一个具有4个参数的递归函数,这4个参数如下所示:
a)备动的盘子数
b)最初放置这些盘子的木桩
c)最后放置这些盘子的木桩
d)作为临时存放点的木桩
关于汉诺塔问题的详细解释,参考文章:
汉诺塔问题简单解释
最初的盘子数n与移动次数moveCount的关系:moveCount=2^(n-1)
程序应该打印出将这些盘子从起始木桩移动到目的木桩所采取的准确步骤。例如,把三个盘子从木桩1移动到木桩3,程序应该打印出如下的移动序列:

代码
#include <bits/stdc++.h>
using namespace std;
int moveCount = 0;
void TowerofHanoi(int, int, int, int);
int main()
{
// int n;
// cout << "请输入盘子的个数:";
// cin >> n;
TowerofHanoi(3, 1, 3, 2);
return 0;
}
void TowerofHanoi(int n, int source, int destination, int auxiliary)
{
if (n == 1)
{
moveCount++;
cout << "第" << moveCount << "步: " << source << " → " << destination << endl;
return; // 此处必须有return语句,否则n会变成负数,从而无法结束递归
}
TowerofHanoi(n - 1, source, auxiliary, destination);
moveCount++;
cout << "第" << moveCount << "步: " << source << " → " << destination << endl;
TowerofHanoi(n - 1, auxiliary, destination, source);
}
运行截图