基于张量变换域低秩正则化的图像恢复方法

news2024/9/24 23:26:21

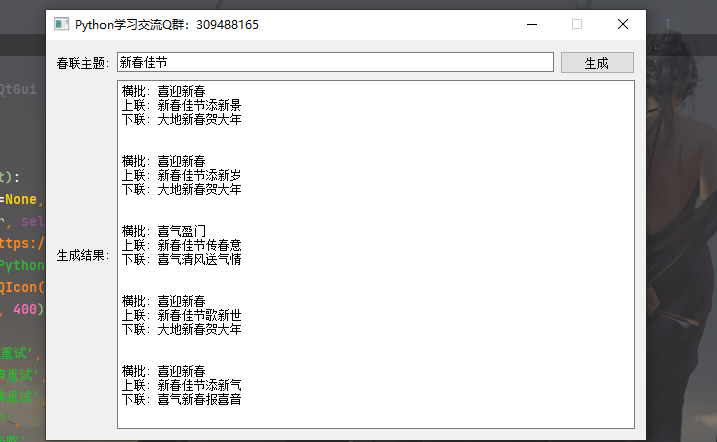
高光谱图像、磁共振图像、RGB图像等都可以表示成三维数组的形式，在数学上将这种多维数组称为高阶张量，同样，上述三种图像都可以表示成三阶张量 $\chi\in \mathbb{R}^{n_{1}\times n_{2}\times n_{3}}$ 。在空间上，图像本身就具有结构相似性，在高光谱图像的第三个模态上，又具有波段上的相关性（MRI、RGB图像都具有相似的性质）。这就使得图像的三阶张量表现出一定的低秩性，因而低秩约束被广泛应用于图像恢复。根据张量的低秩性约束与不同张量秩的定义，又有许多低秩张量补全算法用于图像恢复，比如基于Tucker秩的HaLRTC，基于管秩的TNN，基于TT秩的TMac-TT等。本文将介绍两种TRPCA（Tensor Robust Principal Component Analysis）相关的改进算法，旨在诱导出更低的张量秩。

1. 自适应变换域张量方法(n-TTSVD)

变换域张量的概念最初出现在张量的t-SVD分解中。具体做法如下：

首先，对于张量 $\chi\in \mathbb{R}^{n_{1}\times n_{2}\times n_{3}}$ ，沿着第3模态方向进行矩阵化操作，得到矩阵 $X_{(3)}$ 。然后对矩阵 $X_{(3)}$ 的每一列进行傅里叶变换，并进行张量化操作重新构建一个张量 $\widehat{\chi }$ 。最后，对新张量 $\widehat{\chi }$ 的每一个前部切片进行SVD分解，得到3个因子矩阵， $\widehat{U}^{(i)}$ , $\widehat{S}^{(i)}$ , $\widehat{V}^{(i)}$ , $i=1,\cdots ,n_{3}$ , 再分别又由这3个因子矩阵进行逆傅里叶变换并重新构成3个张量，从而得到了张量的t-SVD分解：，其中，S是f-对角张量。

在张量的t-SVD分解下，定义了张量的核范数，其值为新张量 $\widehat{\chi }$ 的各个前切片的核范数之和：

张量的t-SVD分解中的傅里叶变换是一种正交变换，将此变换推广到更一般的正交变换，由此定义了更一般的变换域张量，并得到了自适应的变换域张量奇异值分解（transformed tensor singular value decomposition, TT-SVD），其过程如下图所示，不同于t-SVD，TT-SVD中的变换不再是傅里叶变换，而是自适应的正交变换T。

首先，对张量的3模展开矩阵做奇异值分解，即：

其中U是 $X_{(3)}$ 的左奇异矩阵，是正交矩阵。

则正交变换由3模展开矩阵的左奇异矩阵的转置构成，即 $T=U^{T}$ 。

在TT-SVD分解下，提出了自适应变换张量核范数[1]：

其中 $\widehat{X}^{(i)}$ 是张量 $\widehat{\chi }$ 的第i个前部切片矩阵，张量 $\widehat{\chi }$ 是张量 $\chi$ 沿着第3个模态做正交变换T得到的变换域张量：，表示对矩阵 $\widehat{X}^{(i)}$ 求核范数。

根据矩阵核范数定义，变换域张量核范数又可以写成：

其中 $\sigma _{l}(X)$ 表示矩阵X的第l个奇异值，r为矩阵 $\widehat{X}^{(i)}$ 的秩。

上述是张量核范数以及变换域张量核范数的定义，仅对张量的第3个模态做了正交变换T，考虑到张量 $\chi$ 有多个模态，徐斌斌等[2]提出了n模自适应变换域张量奇异值分解（n-mode transformed tensor singular value decomposition, n-TTSVD）, 将第三模态的自适应变换矩阵推广到三阶张量的所有模态，其基本流程如下图所示：

首先，对张量的第n个模态展开矩阵进行SVD分解，得到对应的奇异值和左右奇异矩阵：

进而，定义n模自适应的正交变换矩阵为。记 $\widehat{\chi}_{n}$ 为对张量 $\chi$ 第n个模态经过正交变换 $T_{n}$ 得到：。下面给出n-TTSVD的算法描述。

上述方法虽然提出了一种依赖于原始张量并且自适应的变换矩阵的方式，并且将其拓展到三阶张量的所有模态。但是也存在一些缺点：（1）由自适应变换矩阵诱导得到的张量存在能量衰减，但是上面的方法并未给出合理的解决方案，这就导致变换域张量与原张量有较大失真，图像恢复效果也会变差。（2）未提出一个统一的优化框架。由相应的模态展开矩阵的得到变换矩阵，再对其秩进行优化，提高了算法的复杂度。

下面介绍另一种变换域张量低秩正则化的方法——SALTS[3]，该方法将变换矩阵的求解与低秩正则化统一在ADMM框架下求解，并且考虑到了变换后张量的能量损失，并用F范数对其进行约束。

2. 自适应可学习变换域张量方法（SALTS）

与文献2的思路类似，SALTS是SALT算法从第3模态拓展到所有模态得到的，因此，先对SALT方法进行介绍。下面对诱导张量秩进行定义：

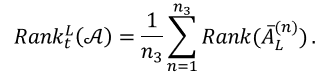
L是可逆线性变换，，是变换域张量第i个前部切片。SALT的目标函数是：

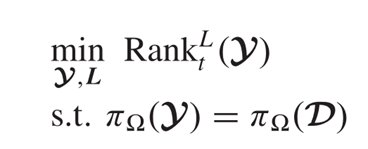
𝒟是观测张量，𝒴是恢复张量，L是变换矩阵。接下来将变换矩阵引入约束，并且考虑到对变换后张量的能量衰减和信息损失，用F范数对其约束：

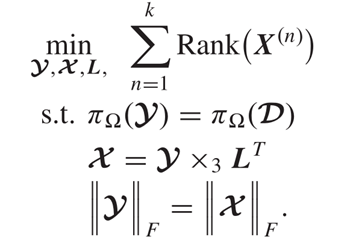
最后，由于秩函数的非凸性，SALT方法用Schatten-p 范数替代RANK():

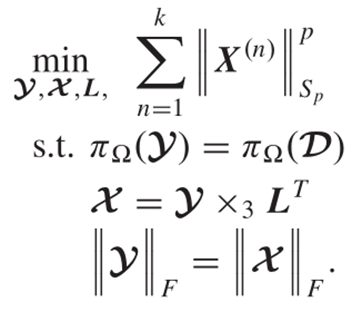
SALTS算法将SALT推广到其他两个模态，并且将三个模态上的优化结果耦合到张量Z：

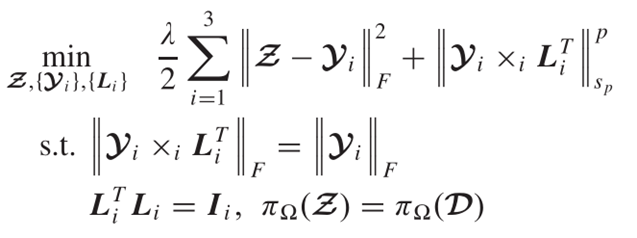
𝒵：恢复的张量；𝒴𝑖：第i个模态被恢复的张量；𝐿𝑖：第i个模态上的变换矩阵。目标函数的第1项是约束恢复的张量𝒵与𝒴𝑖相等，将三个模态的优化结果耦合到一起；第2项：用Schatten-p范数保证变换域张量的低秩性。第1个约束是为了防止变换后张量可能会有能量衰减和信息损失；第2个约束是变换矩阵的需要满足的性质，变换矩阵应该是正交的；最后一个约束是保证张量补全后，已知数据条目的不变。SALTS是利用ADMM框架求解的，下面给出算法的伪代码描述（相关公式参考文献3的proposed methods）：

SALTS算法较基于固定变换矩阵的TNN方法有明显优势，文献[3]给出了变换域张量的奇异值分布对比图：

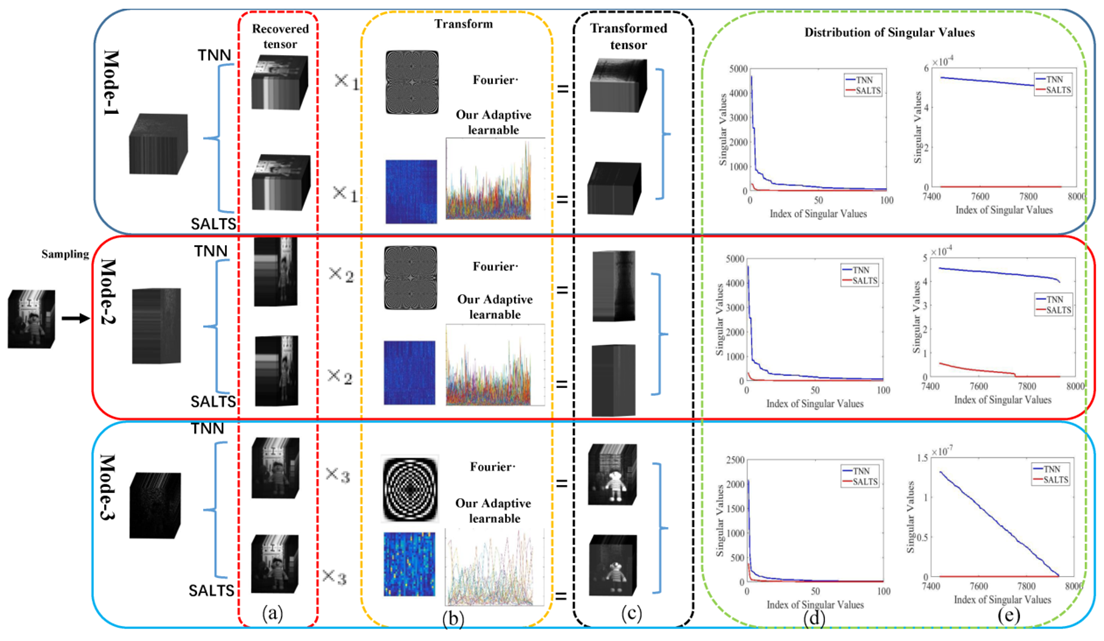
对比图最左边，首先要对原始的光谱图像进行采样，得到观测张量，然后观测张量分别与两种变换矩阵：一个是固定的离散傅里叶变换，另一个是与数据相关的可变变换，进行模态积得到了变换域张量。最后对变换域张量的奇异值进行统计，得到右边的曲线图。曲线图中：张量奇异值是变换域张量前部切片的奇异值，并把这些奇异值按降序排列，横轴是奇异值的索引，纵轴是相对应的奇异值大小。通过对比可以发现：无论在哪个模态，经过SALT处理的张量具有更少的奇异值，并且相应的奇异值也更小。由此，也可以得到SALT算法的一个优势：SALT对方向不敏感，在所有模态下都适用。

[1]Song, Guang-Jing et al. “Robust tensor completion using transformed tensor singular value decomposition.” Numerical Linear Algebra with Applications 27 (2020): n. pag.

[2]徐斌斌. 基于张量变换域低秩正则的高光谱图像去噪研究[D].南京理工大学,2021.DOI:10.27241/d.cnki.gnjgu.2021.000694.

[3]T. Wu, B. Gao, J. Fan, J. Xue and W. L. Woo, "Low-Rank Tensor Completion Based on Self-Adaptive Learnable Transforms," in IEEE Transactions on Neural Networks and Learning Systems, 2022, doi: 10.1109/TNNLS.2022.3215974.

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/140562.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！