归并排序

归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，拍好各数组的顺序，再合并数组。

将数组分解最小之后，然后合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

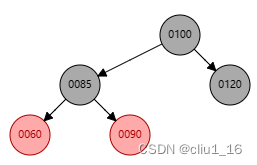
归并排序示意图

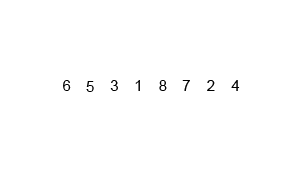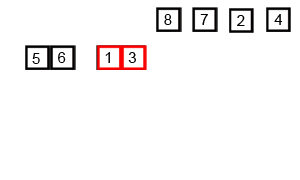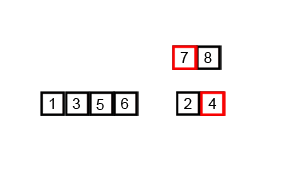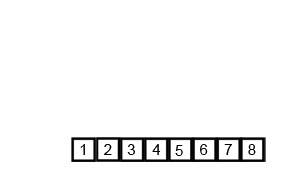
python代码实现-递归版

# 归并排序
def merge_sort(num_list):
    length = len(num_list)
    print(num_list)
    # 递归终止退出条件
    if length <= 1:
        return num_list
    # 拆分
    mid = length // 2  # /2 普通除法，结果为浮点数 //2 整除
    # 对左侧的列表进行排序   1.递归中，左侧数据拆分完才执行下面的
    left_l = merge_sort(num_list[:mid])
    # 对右侧的列表进行排序  2.递归中，右侧数据拆分完才执行下面的
    right_l = merge_sort(num_list[mid:])
    print("left_l：{},right_l：{}".format(left_l, right_l))
    # 3.递归中，上面拆分完了才执行这下面的代码。最初都拆成了一个元素
    # merge 合并操作
    # 初始化两个指针p, q 初始位置为起始位置，初始化一个临时数组temp_list
    p, q, temp_list = 0, 0, list()
    # 计算当前被合并的列表的长度
    len_left, len_right = len(left_l), len(right_l)
    # 对左右两个数组进行排序，用临时数组存储  //p q指针的使用前提是left_l 和right_l是有序的
    while len_left > p and len_right > q:
        if left_l[p] <= right_l[q]:
            temp_list.append(left_l[p])
            p += 1
        else:
            temp_list.append(right_l[q])
            q += 1
    # 如果left 和 right_l 的长度不相等（ len_left > p and len_right > q才排序，q、p达到一方的长度后就停止了，会有一方长的没排），
    temp_list += left_l[p:]
    temp_list += right_l[q:]
    # 把长的部分直接追加到列表中

    return temp_list


if __name__ == '__main__':
    num_list = [6, 5, 3, 1, 8, 7, 2, 4]
    new_list = merge_sort(num_list)
    print('num_list:', new_list)

代码分析

执行过程：

（控制台输出） 先拆分完最左边的->再排完最左边的->再拆分完最右边的->再排完最右边的->左右合并排完最后的
[6, 5, 3, 1, 8, 7, 2, 4]
[6, 5, 3, 1]
[6, 5]
[6]
[5]
left_l：[6],right_l：[5]
[3, 1]
[3]
[1]
left_l：[3],right_l：[1]
left_l：[5, 6],right_l：[1, 3]
[8, 7, 2, 4]
[8, 7]
[8]
[7]
left_l：[8],right_l：[7]
[2, 4]
[2]
[4]
left_l：[2],right_l：[4]
left_l：[7, 8],right_l：[2, 4]
left_l：[1, 3, 5, 6],right_l：[2, 4, 7, 8]
num_list: [1, 2, 3, 4, 5, 6, 7, 8]

执行步骤

第一步：拆分，除2除2不断的二分。分到不能分后开始排序。拆分过程如上。(所以递归层数为：log(底数2)（指数n）)
第二步：排序，设定两个指针，最初位置分别为两个已经排序（重点）序列的起始位置
第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
第四步：重复第三步直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾，完成一轮排序

时间复杂度

拆分的过程中不断二分，因此递归层数为：log(底数2)（指数n）
每层循环大约为：n次
时间复杂度为：O(nlogn)

非递归版

def merge_sort(num_list):
    length = len(num_list)
    if length <= 1:
        return num_list

    # 使用循环代替递归
    step = 1 # 从1开始 不断×2和递归版拆分相反
    while step < length:
        left = 0
        while left < length - step:
            print("left：{}".format(left))
            mid = left + step
            right = min(left + 2 * step, length)
            temp_list = merge(num_list[left:mid], num_list[mid:right])
            num_list[left:left + len(temp_list)] = temp_list  # 将归并排序中合并得到的有序列表 temp_list 更新到原始列表 num_list 的相应位置。
            left += 2 * step
        step *= 2
        print("step：{}".format(step))
    return num_list


def merge(left_list, right_list):
    p, q, temp_list = 0, 0, list()

    while p < len(left_list) and q < len(right_list):
        if left_list[p] <= right_list[q]:
            temp_list.append(left_list[p])
            p += 1
        else:
            temp_list.append(right_list[q])
            q += 1

    temp_list += left_list[p:]
    temp_list += right_list[q:]

    return temp_list


if __name__ == '__main__':
    num_list = [6, 5, 3, 1, 8, 7, 2, 4]
    new_list = merge_sort(num_list)
    print('num_list:', new_list)

在归并排序的循环实现中，step、left、mid 和 right 是循环中的一些变量，它们有以下含义：

1. step（步长）:

   • step 是归并排序中的步长，它表示每次迭代中子数组的大小。循环的外部使用 while step < length 来不断增加步长，直到步长超过列表长度。

2. left（左指针）:

   • left 是指向当前子数组的起始位置的指针。在循环内，left 的值随着每次子数组合并而增加。

3. mid（中间指针）:

   • mid 是当前子数组的中间位置的指针。在归并排序中，每次合并两个有序子数组时，mid 用于确定左右两个子数组的边界。

4. right（右指针）:

   • right 是指向当前子数组的结束位置的指针。在循环内，right 的值随着每次子数组合并而增加。

下面是循环中涉及这些变量的核心代码：

step = 1
while step < length:
    left = 0
    while left < length - step:
        mid = left + step
        right = min(left + 2 * step, length)
        temp_list = merge(num_list[left:mid], num_list[mid:right])
        num_list[left:left + len(temp_list)] = temp_list
        left += 2 * step
    step *= 2

在外循环中，step 不断翻倍，内循环中，left 指向当前子数组的起始位置，mid 指向中间位置，right 指向结束位置。temp_list 存储合并后的有序子数组，然后通过切片操作将其更新到原始列表 num_list 中的相应位置。随着循环的进行，left 不断增加，表示下一个子数组的起始位置，直到整个列表有序。