岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

 方法

深度优先遍历

网格问题的基本概念

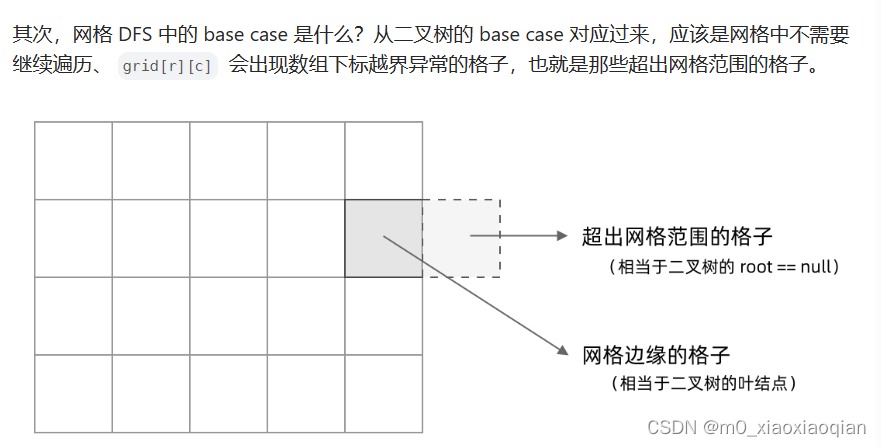
避免重复遍历：

使用标记

以岛屿问题为例，我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子，就把格子的值改为 2，这样当我们遇到 2 的时候，就知道这是遍历过的格子了。也就是说，每个格子可能取三个值：

• 0 —— 海洋格子
• 1 —— 陆地格子（未遍历过）
• 2 —— 陆地格子（已遍历过）

代码一

统计网格中字符 '1' 出现的次数

class Solution {
    // 深度优先遍历 参考二叉树的DFS  图/网格  四叉
    public int numIslands(char[][] grid) {
        // 定义count 用于统计岛屿的数量
        int count = 0;
        // 遍历网格
        for(int r = 0; r < grid.length; r++){
            for(int c = 0 ; c < grid[0].length; c++){
                // 若当前网格的值为“1”，则为陆地，遍历其的上下左右
                if(grid[r][c] == '1'){
                    // 调用递归函数
                    dfsHelp(grid, r, c);
                    // 统计岛屿数量 由多个陆地组成
                    count ++;
                }
            }
        }
        // 返回结果
        return count;
        
    }

    // 递归函数
    public void dfsHelp(char[][] grid, int row, int column){
        // 递归出口 防止网格越界
        if(row < 0 || column < 0 || (row >= 0 && row < grid.length) || (column >= 0 && column < grid[0].length)){
            return;
        }
        // 若网格为海洋 即值为"0"时 或者值为"2"时，也退出
        if(grid[row][column] == '0'|| grid[row][column] == '2'){
            return ;
        }
        // 将遍历过的陆地1 标记为2
        grid[row][column] = '2';

        // 递归遍历
        dfsHelp(grid, row - 1, column);   // 上
        dfsHelp(grid, row + 1, column);   // 下
        dfsHelp(grid, row, column -1);    // 左
        dfsHelp(grid, row, column +1);    // 右

    }
}

代码二

修改之后的代码

class Solution {
    // 深度优先遍历 参考二叉树的DFS  图/网格  四叉
    public int numIslands(char[][] grid) {
        // 首先对网格进行判空
        if(grid == null || grid.length == 0){
            return 0;
        }
        // 定义count 用于统计岛屿的数量
        int count = 0;
        // 遍历网格
        for(int r = 0; r < grid.length; r++){
            for(int c = 0 ; c < grid[0].length; c++){
                // 若当前网格的值为“1”，则为陆地，遍历其的上下左右
                if(grid[r][c] == '1'){
                    // 调用递归函数
                    dfsHelp(grid, r, c);
                    // 统计岛屿数量 由多个陆地组成
                    count ++;
                }
            }
        }
        // 返回结果
        return count;
        
    }
 
    // 递归函数
    public void dfsHelp(char[][] grid, int row, int column){
        // 递归出口 防止网格越界
        if(row < 0 || column < 0 || row >= grid.length || column >= grid[0].length){
            return;
        }
        // 若网格为海洋 即值为"0"时 或者值为"2"时，即值不等于1时 也退出
        if(grid[row][column] != '1'){
            return ;
        }
        // 将遍历过的陆地1 标记为2
        grid[row][column] = '2';
 
        // 递归遍历
        dfsHelp(grid, row - 1, column);   // 上
        dfsHelp(grid, row + 1, column);   // 下
        dfsHelp(grid, row, column -1);    // 左
        dfsHelp(grid, row, column +1);    // 右
 
    }
}