来源：德思特测量测试 德思特干货｜如何使用SBench 6对数字化仪采集信号进行处理？（三）——快速傅立叶变换（FFT）

原文链接：https://mp.weixin.qq.com/s/mYS1iDXFNVfReCGGtF78mw

欢迎关注虹科，为您提供最新资讯！

#信号采集 #信号处理 #测量测试

上一篇文章介绍了德思特SBench 6的平均运算功能。本章将继续为大家介绍SBench 6的快速傅立叶变换（FFT）。

前文回顾：https://mp.weixin.qq.com/s/j-iN_2Jrn9ZHGMaaAYsDJg

快速傅立叶变换（FFT）

快速傅立叶变换（FFT）将获取的波形从时域（幅度对时间）映射到频谱域（幅度对频率）。这使得用户可以观察构成信号的频率成分。FFT本身并不能直接改善信号质量，但它能显示信号的频率成分结构，并提供了如何移除不需要的频谱成分的信息。

FFT产生的频谱有一个离散的时间轴，就像时域信号有离散的采样时间一样。频谱中的谱线，通常称为“bins”或“cells”，每个谱线之间由分辨率带宽（f）隔开，而分辨率带宽与采集到的原始信号长度成反比，因此，要增加FFT频谱的频率分辨率，必须增加采集的原始信号长度。而频谱显示的总频率范围，或者说频率跨度，是原始信号采样率的一半，因此，要增加总频率跨度，也必须增加采样率。

在德思特SBench 6软件中，FFT结果的纵轴缩放可以设为线性单位伏特，也可以是对数单位分贝（dB）。对数刻度可以参考数字化仪的满偏刻度（dBFS）、1 毫瓦（dBm）、1 微伏（dbμV）或设为针对假定载波频谱中的最大峰值（dBc）。

（1）权重函数

理论上的傅立叶变换假设输入记录的长度为无穷大。有限的采样长度则会在频域边缘引入不连续性，为频域引入伪频率，并一定程度扭曲实际的频谱。例如，当信号的开始和结束相位不同，或者信号频率落在两个相邻的谱线之间时，使频谱变宽。

频谱展宽，以至于扩展到许多相邻的频带，称为泄漏。对于这种问题的理论应对方法是确保在显示网格内包含整数个周期，或在边缘处不出现不连续性。两者都需要信号波形频率和数字化采样率之间非常精确的同步，并且需要准确地设置采集长度，这通常只可能在实验室中实现，而不能作用于真实世界的信号。另一种方法是使用窗函数（加权）来平滑信号的边缘。

为了尽量减少这些负面影响，对获取的信号应用加权函数，使记录的端点为零。德思特SBench 6软件中的FFT功能为用户提供八种加权函数的选择，而这些加权函数则可以改变谱线的形状。对此没什么概念的读者，可以把它想象为组合到一起的一些列并行的理想带通滤波器，这些滤波器之间的频率间距为分辨率带宽，而加权函数则会影响滤波器频率响应的形状。图1比较了四种最常用的加权函数对应的频率响应。

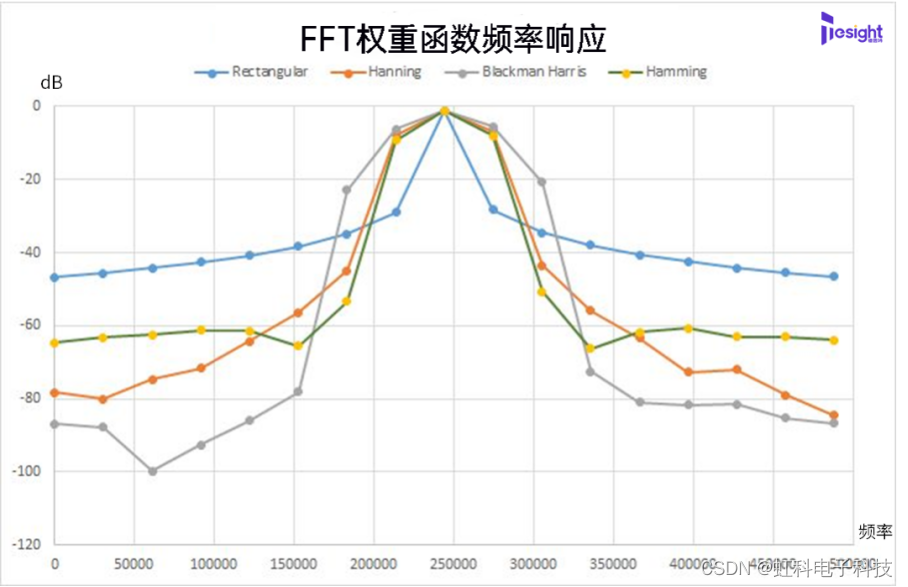
图1：四种最常用的加权函数的谱形状比较

理想情况下，主瓣应尽可能窄，且两侧平坦，以代表真实的频谱成分，而所有旁瓣应无限衰减。窗函数类型定义了在FFT处理中使用的等效滤波器的带宽和形状。表1中展示了频谱响应的最大旁瓣幅度。较大的旁瓣电平将有助于区分密集的频谱成分。

表1：不同加权函数的关键特性

如前所述，FFT结果的频率轴是离散的，具有以分辨率带宽的倍数间隔的频点。如果输入信号频率落在两个相邻的谱线之间，能量将被分配到两个谱线中，且峰值幅度将降低。这被称为栅栏效应或波浪状效应，而扩宽频谱响应可以减少幅度变化。表1中的栅栏损失列给出了不同加权函数该效应幅值。

同时，加权函数还会影响频谱响应的带宽。等效噪声带宽（ENBW）说明了相对于矩形窗加权带宽的相对变化。将功率谱归一化到测量带宽（功率谱密度）需要将功率谱除以ENBW与分辨率带宽的积（f✖️ENBW）。

相干增益描述了给定加权函数相对于矩形窗加权的频谱幅度变化。这是一个应用在所有频率上的固定增益，可以很容易地归一化。

矩形窗加权函数是采集信号没有任何加权的响应。它具有最窄的带宽，但旁瓣幅值则相当高。由于采集时域记录中的所有点的幅度响应都是均匀的，它常用于具有瞬态性质的信号（或相对记录总长短得多的信号）。当需要以最佳频率精度进行分析时，也会使用它。

Hanning和Hamming加权函数具有良好的通用的频率响应，能提供较好的频率分辨率以及合理的旁瓣响应。Blackman-Harris则旨在获得最佳幅度精度和优秀的旁瓣抑制。

（2）FFT应用实例

图2展现了一个典型的FFT应用实例。在该实例中，我们使用宽带的仪器级麦克风和德思特TS-M4i系列14位数字化仪，获得了超声波测距仪的信号。

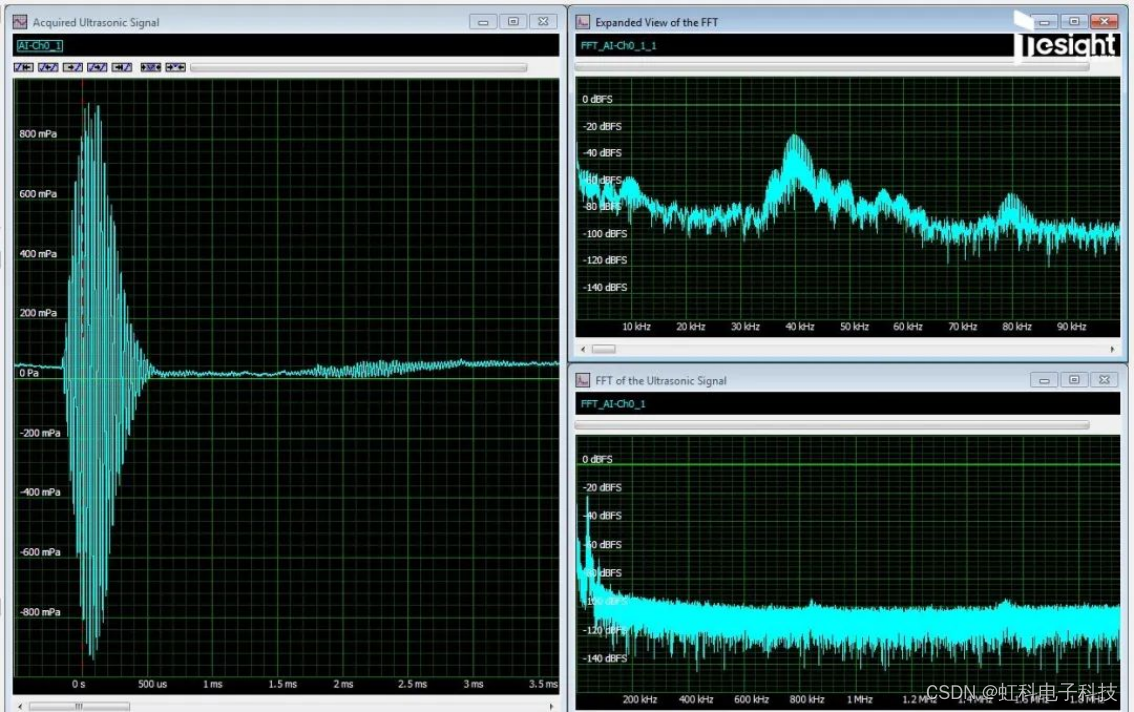
图2：40 kHz的超声波脉冲（左）及其FFT结果（右下全频段，右上局部放大）

采集到的时域信号在左窗格中。时域记录包含了在3.90625 MS/s采样率下采集到的16384个样本点，持续时间为4.2毫秒。得到的FFT结果（右窗格）共有8192条谱线，每条谱线之间间隔238 Hz分辨率带宽（记录时长的倒数），总频率跨度为1.95 MHz（采样率的一半）。其中，右下角的频谱是全频段总览图，右上角则是局部放大视图，只显示了前100 kHz频率范围的内容，以便更好地观察主要频谱成分。

FFT能帮助我们更好地理解构成这个信号的成分。首先我们看时域，可以知道这是一个持续时间小于采集记录长度的瞬态信号，在这种情况下我们选用了矩形窗进行加权。FFT结果中幅值最大的频率成分，明显就是我们的主要信号——40 kHz左右的脉冲。而在80 kHz附近频率的一个小峰，则是40 kHz信号成分的二次谐波。其幅度大约比40 kHz信号成分低45 dB。此外，在0~10 kHz之间也有很多低频干扰成分，其中最高的、接近DC的那部分，对应的是设备所在房间中的环境噪声。

在该实例中，我们的目标是能够测量发射脉冲和40 kHz回波之间的时延。为了实现这一点，我们需要改进这个测量过程。第一步，我们希望移除频谱中40 kHz成分之外的其它成分。现在我们将带着这个目标，来进行滤波器的设置。

（3）滤波

在德思特SBench 6专业版软件中，我们提供了低通、带通或高通选项的有限冲激响应(FIR)数字滤波器。通过输入所需的滤波器类型、截止频率或频率，以及滤波器阶数，用户可以直接在图形界面中创建这些滤波器。SBench 6软件会在滤波器无法实现时给出提示，并提出解决建议。或者，您也可以输入从其他来源获取的滤波器系数。我们将这些滤波器应用于采集到的信号，然后将滤波结果与原始采样结果或平均采样结果进行比较。在图3中，应用的带通FIR滤波器截止频率为30和50 kHz，以帮助提取目标信号。

图3：原始波形和滤波后信号及其FFT结果的对比

左上角的窗格显示了原始波形，下面对应我们之前看到的原始信号FFT结果。右上角的窗格则为通过带通滤波后的波形，滤波信号的FFT结果在右下角的窗格中。可以发现，带通滤波器消除了低频拾取噪声和80 kHz位置的二次谐波。滤波后的信号在时间域视图现在有了一个相对平坦的基线，从而能使反射信号更清楚地分辨出来，而这就是我们滤波处理的目标。由此我们也可以看出FFT对深入了解信号提供的帮助。

结论

使用德思特SBench 6软件提供的信号处理工具，如模拟运算、平均值、FFT、滤波和直方图等，将有助于加深对采集信号的见解，此外，还能生成一系列有利于进一步分析的二级信号波形。