在编程中,处理二维数组的问题可以有多种解法。今天,我们将探讨两种解决“顺时针打印矩阵”问题的方法:偏移量法和边界控制法,并进行比较。
题目
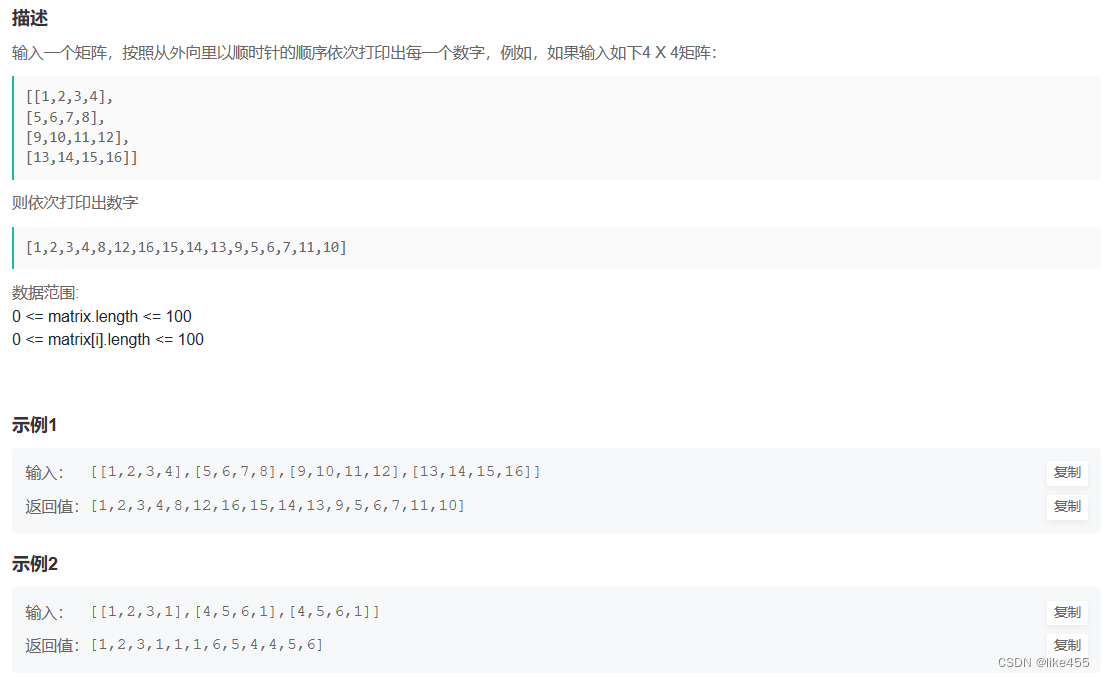
题目连接:顺时针打印矩阵_牛客题霸_牛客网 (nowcoder.com)
偏移量法
偏移量法的核心思想是使用两个数组来控制遍历方向。这种方法特别适合于遍历二维空间时的方向控制。
代码实现
import java.util.ArrayList;
import java.util.List;
public class Solution {
// 定义dx和dy为静态数组,表示四个方向的偏移量:上,右,下,左
private static final int[] dx = {-1, 0, 1, 0};
private static final int[] dy = {0, 1, 0, -1};
public List<Integer> printMatrix(int[][] matrix) {
List<Integer> res = new ArrayList<>();
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return res;
int n = matrix.length, m = matrix[0].length;
boolean[][] st = new boolean[n][m]; // st数组用于标记已访问的位置
int x = 0, y = 0, d = 1; // 初始位置(0,0)和方向(向右)
for (int k = 0; k < n * m; k++) {
res.add(matrix[x][y]); // 添加当前元素
st[x][y] = true; // 标记为已访问
// 计算下一个位置
int a = x + dx[d], b = y + dy[d];
// 判断边界和是否已访问
if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) {
d = (d + 1) % 4; // 改变方向
a = x + dx[d];
b = y + dy[d];
}
x = a;
y = b;
}
return res;
}
}
解释:
偏移量按照“上、右、下、左”的顺序来定义的。这个顺序决定了遍历矩阵的方向。
在代码中:
-
dx = {-1, 0, 1, 0}表示行的变化。 -
dy = {0, 1, 0, -1}表示列的变化。
这里的偏移量对应的遍历方向是:
-
向上(dx = -1, dy = 0)。
-
向右(dx = 0, dy = 1)。
-
向下(dx = 1, dy = 0)。
-
向左(dx = 0, dy = -1)。
在遍历过程中,通过改变d的值来选择不同的偏移量,从而改变遍历的方向。遍历始于向右方向(d = 1),并在遇到边界或已访问的元素时顺时针旋转到下一个方向。
这种方法特别适合处理这类二维数组遍历的问题。通过简单地调整偏移量数组,可以轻松地更改遍历的方向或模式,适应各种不同的需求和场景。
如何定义dx、dy数组?
矩阵遍历使用的x和y的定义有些特殊。通常,在数学和计算机图形学中,我们习惯于将x轴定义为水平方向,y轴定义为垂直方向。然而,在二维数组或矩阵的上下文中,这些轴的定义通常与传统的笛卡尔坐标系有所不同。
在代码中
-
x变量代表的是二维数组的行索引。 -
y变量代表的是二维数组的列索引。
然而,
-
当我们说“向上”移动时,实际上是在减少
x的值(因为在数组中向上移动意味着向更小的行索引移动)。 -
同样,"向右"移动实际上是增加
y的值(在数组中向右移动意味着向更大的列索引移动)。 -
“向下”移动是增加
x的值。 -
“向左”移动是减少
y的值。
这种定义方式是基于二维数组的索引,其中matrix[x][y]表示位于第x行和第y列的元素。所以,尽管这种定义方式可能与传统的笛卡尔坐标系不同,但它完全适合于二维数组或矩阵的遍历操作。
我的这篇 使用邻接点偏移量数组解决 BFS 类问题-CSDN博客 博客同样讲解了这类问题
优势与局限性
优势:
-
代码简洁:整个遍历过程可以在一个循环中完成。
-
方向控制灵活:通过改变索引即可改变方向,适用于复杂路径的遍历。
局限性:
-
需要额外状态数组:用于记录哪些元素已被访问。
-
边界处理稍复杂:需要检查下一个位置是否越界或已访问。
边界控制法
边界控制法通过定义上下左右边界来控制遍历过程。
代码实现
import java.util.ArrayList;
public class Solution {
public ArrayList<Integer> printMatrix(int [][] matrix) {
ArrayList<Integer> res = new ArrayList<>();
//先排除特殊情况
if(matrix.length == 0) {
return res;
}
//左边界
int left = 0;
//右边界
int right = matrix[0].length - 1;
//上边界
int up = 0;
//下边界
int down = matrix.length - 1;
//直到边界重合
while(left <= right && up <= down){
//上边界的从左到右
for(int i = left; i <= right; i++)
res.add(matrix[up][i]);
//上边界向下
up++;
if(up > down)
break;
//右边界的从上到下
for(int i = up; i <= down; i++)
res.add(matrix[i][right]);
//右边界向左
right--;
if(left > right)
break;
//下边界的从右到左
for(int i = right; i >= left; i--)
res.add(matrix[down][i]);
//下边界向上
down--;
if(up > down)
break;
//左边界的从下到上
for(int i = down; i >= up; i--)
res.add(matrix[i][left]);
//左边界向右
left++;
if(left > right)
break;
}
return res;
}
}
优势与局限性
优势:
-
直观明了:逻辑清晰,易于理解和维护。
-
无需额外状态数组:直接通过边界控制实现遍历。
局限性:
-
多个循环:每个方向的遍历需要独立的循环。
-
边界更新逻辑:每完成一个方向,都需要更新边界。
总结
两种方法各有优缺点。偏移量法在代码简洁性和灵活性方面更优,但需要额外的状态数组来跟踪已访问的元素。边界控制法则在逻辑清晰度上占优,但涉及多个循环和边界更新的逻辑。
就我各个人来讲。把算法题抽象成通用模板确实可以提高解题效率,特别是对于那些有固定模式或可复用逻辑的问题。使用偏移量方法解决矩阵遍历类问题是一个很好的例子。这种方法不仅提供了一种清晰、灵活的方式来处理二维空间的遍历,还可以轻松应对多种不同的遍历要求,比如螺旋遍历、波形遍历等。
偏移量法的模板化
偏移量法的核心在于定义一组方向向量,通过这些向量控制遍历的方向。这种方法的模板化可以分为以下几个步骤:
-
定义方向向量:创建两个数组,一个表示行的偏移(dx),另一个表示列的偏移(dy)。例如,对于上、右、下、左的顺时针方向,可以定义
dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1}。 -
初始化遍历状态:设置起始点和初始方向,通常从(0,0)点开始,方向设置为向右。
-
遍历矩阵:使用一个循环进行遍历,每次移动后检查边界和是否已访问,必要时改变方向。
-
边界和访问状态检查:在每次移动后,检查下一个位置是否超出矩阵边界或者已经访问过。如果是,改变方向。
这种模板化方法在处理各种矩阵遍历问题时具有明显优势:
- 可重用性:一旦掌握了这个模板,就可以快速应用到类似的问题上。
- 灵活性:通过调整方向向量,可以轻松适应不同的遍历要求。
- 简洁性:代码更加简洁,易于理解和维护。