C++面试：跳表

news2025/4/19 8:37:57

        

目录

跳表介绍 

跳表的特点：

跳表的应用场景：

C++ 代码示例：

跳表的特性

跳表示例 

总结

        跳表（Skip List）是一种支持快速搜索、插入和删除的数据结构，具有相对简单的实现和较高的查询性能。下面是跳表的详细介绍和一个简单的 C++ 代码示例：

跳表介绍 

跳表的特点：

  1. 有序结构： 跳表中的每个节点都包含一个元素，并且节点按照元素的大小有序排列。
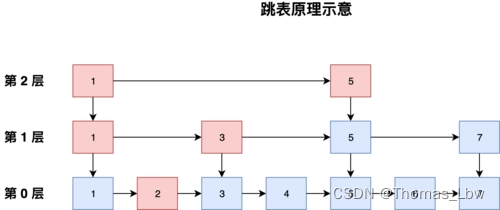
  2. 多层索引： 跳表通过维护多层索引来实现快速搜索。每一层都是一个有序链表，最底层包含所有元素，而每上一层的节点是下一层节点的一部分。
  3. 跳跃式访问： 通过索引层，跳表允许在较高层直接跳过一些节点，从而提高搜索效率。

跳表的应用场景：

  1. 有序集合的实现： 用于需要频繁的插入、删除和搜索操作的有序数据集合，如 Redis 中的有序集合（Sorted Set）。
  2. 替代平衡树： 在某些场景下，跳表可以作为对平衡树的一种替代，具有更简单的实现和较好的性能。

C++ 代码示例：

#include <iostream>
#include <vector>
#include <cstdlib>

const int MAX_LEVEL = 16;  // 最大层数

// 跳表节点定义
struct Node {
    int value;
    std::vector<Node*> forward;  // 每层的指针数组

    Node(int val, int level) : value(val), forward(level, nullptr) {}
};

// 跳表定义
class SkipList {
private:
    Node* header;  // 头节点
    int level;     // 当前跳表的最大层数

public:
    SkipList() : level(1) {
        header = new Node(0, MAX_LEVEL);
    }

    // 随机生成一个层数
    int randomLevel() {
        int lvl = 1;
        while ((rand() % 2) && (lvl < MAX_LEVEL))
            lvl++;
        return lvl;
    }

    // 插入一个元素
    void insert(int val) {
        std::vector<Node*> update(MAX_LEVEL, nullptr);
        Node* current = header;

        // 从最高层到底层，找到每一层的插入位置
        for (int i = level - 1; i >= 0; i--) {
            while (current->forward[i] != nullptr && current->forward[i]->value < val) {
                current = current->forward[i];
            }
            update[i] = current;
        }

        // 随机生成一个层数
        int newLevel = randomLevel();

        // 如果新的层数比当前层数高，则更新 update
        if (newLevel > level) {
            for (int i = level; i < newLevel; i++) {
                update[i] = header;
            }
            level = newLevel;
        }

        // 创建新节点
        Node* newNode = new Node(val, newLevel);

        // 更新每一层的指针
        for (int i = 0; i < newLevel; i++) {
            newNode->forward[i] = update[i]->forward[i];
            update[i]->forward[i] = newNode;
        }
    }

    // 搜索一个元素，返回是否存在
    bool search(int val) {
        Node* current = header;

        // 从最高层到底层，搜索每一层的节点
        for (int i = level - 1; i >= 0; i--) {
            while (current->forward[i] != nullptr && current->forward[i]->value < val) {
                current = current->forward[i];
            }
        }

        // 到达底层，判断是否找到目标元素
        if (current->forward[0] != nullptr && current->forward[0]->value == val) {
            return true;
        } else {
            return false;
        }
    }

    // 删除一个元素
    void remove(int val) {
        std::vector<Node*> update(MAX_LEVEL, nullptr);
        Node* current = header;

        // 从最高层到底层，找到每一层的删除位置
        for (int i = level - 1; i >= 0; i--) {
            while (current->forward[i] != nullptr && current->forward[i]->value < val) {
                current = current->forward[i];
            }
            update[i] = current;
        }

        // 到达底层，判断是否找到目标元素
        if (current->forward[0] != nullptr && current->forward[0]->value == val) {
            // 更新每一层的指针，删除目标节点
            for (int i = 0; i < level; i++) {
                if (update[i]->forward[i] != current->forward[i]) {
                    break;
                }
                update[i]->forward[i] = current->forward[i]->forward[i];
            }

            // 如果删除的是最高层的节点，更新层数
            while (level > 1 && header->forward[level - 1] == nullptr) {
                level--;
            }

            // 释放节点内存
            delete current;
        }
    }

    // 打印跳表
    void printSkipList() {
        for (int i = level - 1; i >= 0; i--) {
            Node* current = header->forward[i];
            std::cout << "Level " << i << ": ";
            while (current != nullptr) {
                std::cout << current->value << " ";
                current = current->forward[i];
            }
            std::cout << std::endl;
        }
        std::cout << "-----------------------" << std::endl;
    }
};

int main() {
    // 创建跳表
    SkipList skipList;

    // 插入一些元素
    skipList.insert(3);
    skipList.insert(6);
    skipList.insert(7);
    skipList.insert(9);
    skipList.insert(12);

    // 打印跳表
    skipList.printSkipList();

    // 搜索元素
    int searchValue = 7;
    if (skipList.search(searchValue)) {
        std::cout << "Element " << searchValue << " found in the skip list." << std::endl;
    } else {
        std::cout << "Element " << searchValue << " not found in the skip list." << std::endl;
    }

    // 删除元素
    int removeValue = 6;
    skipList.remove(removeValue);

    // 打印删除后的跳表
    skipList.printSkipList();

    return 0;
}

        这是一个简单的跳表实现，包括插入、搜索和删除操作。在实际应用中，跳表的层数、随机层数的方式以及其他细节可以根据具体需求进行调整。

跳表的特性

  1. 有序性： 跳表中的每个节点按照元素的大小有序排列。这使得在跳表中可以快速定位和搜索元素。

  2. 多层索引： 跳表通过维护多层索引来实现快速搜索。每一层都是一个有序链表，最底层包含所有元素，而每一层的节点是下一层节点的子集。这样的多层索引结构可以提高搜索效率。

  3. 跳跃式访问： 通过多层索引，跳表允许在较高层直接跳过一些节点，从而实现跳跃式的访问。这种设计类似于在二分查找中直接跳过一半的元素，从而提高了搜索的效率。

  4. 平衡性： 跳表的设计通过随机层数和灵活的插入策略，保持了跳表的平衡性。这有助于避免类似于二叉搜索树中的不平衡情况，使得操作的时间复杂度更加可控。

  5. 简单实现： 跳表相对于其他高效的数据结构，如平衡树，实现相对简单。它不需要像平衡树那样复杂的平衡维护，使得代码的实现和维护相对容易。

  6. 支持动态操作： 跳表天生适合动态操作，包括插入和删除。由于插入和删除操作只需要调整相邻节点的指针，而不需要进行全局的平衡调整，因此操作的效率较高。

  7. 适应范围广： 跳表可以应用于各种有序数据集合的场景，特别是在需要频繁插入、删除和搜索操作的场景中，其性能表现优异。

        跳表的这些特性使得它在一些应用场景中具有明显的优势，尤其在无法提前知道数据分布情况的情形下，跳表能够以较简单的方式维护有序性和高效操作。

跳表示例 

        下面是一个使用 C++ 实现的跳表例子，包含插入、搜索、删除和打印操作。在这个例子中，我使用了模板类以支持不同类型的元素。

#include <iostream>
#include <vector>
#include <cstdlib>

// 跳表节点定义
template <typename T>
struct Node {
    T value;
    std::vector<Node*> forward;

    Node(T val, int level) : value(val), forward(level, nullptr) {}
};

// 跳表定义
template <typename T>
class SkipList {
private:
    Node<T>* header;
    int level;

public:
    SkipList() : level(1) {
        header = new Node<T>(T(), MAX_LEVEL);  // 初始值为 T() 的头节点
    }

    // 随机生成一个层数
    int randomLevel() {
        int lvl = 1;
        while ((rand() % 2) && (lvl < MAX_LEVEL))
            lvl++;
        return lvl;
    }

    // 插入一个元素
    void insert(const T& val) {
        std::vector<Node<T>*> update(MAX_LEVEL, nullptr);
        Node<T>* current = header;

        // 从最高层到底层，找到每一层的插入位置
        for (int i = level - 1; i >= 0; i--) {
            while (current->forward[i] != nullptr && current->forward[i]->value < val) {
                current = current->forward[i];
            }
            update[i] = current;
        }

        // 随机生成一个层数
        int newLevel = randomLevel();

        // 如果新的层数比当前层数高，则更新 update
        if (newLevel > level) {
            for (int i = level; i < newLevel; i++) {
                update[i] = header;
            }
            level = newLevel;
        }

        // 创建新节点
        Node<T>* newNode = new Node<T>(val, newLevel);

        // 更新每一层的指针
        for (int i = 0; i < newLevel; i++) {
            newNode->forward[i] = update[i]->forward[i];
            update[i]->forward[i] = newNode;
        }
    }

    // 搜索一个元素，返回是否存在
    bool search(const T& val) const {
        Node<T>* current = header;

        // 从最高层到底层，搜索每一层的节点
        for (int i = level - 1; i >= 0; i--) {
            while (current->forward[i] != nullptr && current->forward[i]->value < val) {
                current = current->forward[i];
            }
        }

        // 到达底层，判断是否找到目标元素
        return (current->forward[0] != nullptr && current->forward[0]->value == val);
    }

    // 删除一个元素
    void remove(const T& val) {
        std::vector<Node<T>*> update(MAX_LEVEL, nullptr);
        Node<T>* current = header;

        // 从最高层到底层，找到每一层的删除位置
        for (int i = level - 1; i >= 0; i--) {
            while (current->forward[i] != nullptr && current->forward[i]->value < val) {
                current = current->forward[i];
            }
            update[i] = current;
        }

        // 到达底层，判断是否找到目标元素
        if (current->forward[0] != nullptr && current->forward[0]->value == val) {
            // 更新每一层的指针，删除目标节点
            for (int i = 0; i < level; i++) {
                if (update[i]->forward[i] != current->forward[i]) {
                    break;
                }
                update[i]->forward[i] = current->forward[i]->forward[i];
            }

            // 如果删除的是最高层的节点，更新层数
            while (level > 1 && header->forward[level - 1] == nullptr) {
                level--;
            }

            // 释放节点内存
            delete current;
        }
    }

    // 打印跳表
    void printSkipList() const {
        for (int i = level - 1; i >= 0; i--) {
            Node<T>* current = header->forward[i];
            std::cout << "Level " << i << ": ";
            while (current != nullptr) {
                std::cout << current->value << " ";
                current = current->forward[i];
            }
            std::cout << std::endl;
        }
        std::cout << "-----------------------" << std::endl;
    }
};

int main() {
    // 创建跳表
    SkipList<int> skipList;

    // 插入一些元素
    skipList.insert(3);
    skipList.insert(6);
    skipList.insert(7);
    skipList.insert(9);
    skipList.insert(12);

    // 打印跳表
    skipList.printSkipList();

    // 搜索元素
    int searchValue = 7;
    if (skipList.search(searchValue)) {
        std::cout << "Element " << searchValue << " found in the skip list." << std::endl;
    } else {
        std::cout << "Element " << searchValue << " not found in the skip list." << std::endl;
    }

    // 删除元素
    int removeValue = 6;
    skipList.remove(removeValue);

    // 打印删除后的跳表
    skipList.printSkipList();

    return 0;
}

在这个例子中，使用跳表有几个考虑因素：

  1. 高效的搜索操作： 跳表的搜索操作时间复杂度为 O(log n)，其中 n 是跳表中的元素个数。相较于普通链表的线性搜索，跳表提供了更快的搜索速度。

  2. 支持动态操作： 跳表天生适合动态操作，包括插入和删除。由于插入和删除操作只需要调整相邻节点的指针，而不需要进行全局的平衡调整，因此在元素的动态更新场景下，跳表相对于其他数据结构更具有优势。

  3. 简单实现： 跳表的实现相对简单，不需要像平衡树那样复杂的平衡维护。这使得它在实际应用中更容易实现和维护。

  4. 对比其他数据结构： 在这个示例中，使用跳表的主要目的是演示跳表的基本原理和操作，并不代表它是绝对优于其他数据结构的选择。具体选择数据结构的决策取决于实际应用场景、数据分布情况以及对不同操作的需求。

总结

特性:

  1. 有序性： 跳表中的每个节点按照元素的大小有序排列，使得在跳表中可以快速定位和搜索元素。
  2. 多层索引： 跳表通过维护多层索引来实现快速搜索，每一层都是一个有序链表，最底层包含所有元素。
  3. 跳跃式访问： 通过多层索引，跳表允许在较高层直接跳过一些节点，实现跳跃式的访问，提高搜索效率。
  4. 平衡性： 通过随机层数和灵活的插入策略，保持了跳表的平衡性，避免了类似于二叉搜索树中的不平衡情况。
  5. 支持动态操作： 跳表天生适合动态操作，包括插入和删除，操作的时间复杂度较低。

应用场景:

  1. 有序集合的实现： 适用于需要频繁插入、删除和搜索操作的有序数据集合，例如在 Redis 中的有序集合（Sorted Set）实现中使用了跳表。
  2. 替代平衡树： 在某些场景下，跳表可以作为对平衡树的一种替代，相对简单的实现和较好的性能表现使得它成为一种备选选择。
  3. 动态数据库索引： 在数据库中，跳表可以用作动态索引结构，适用于动态更新和频繁搜索的情况。
  4. 高效的动态排序： 在需要频繁的动态排序操作的场景下，跳表的性能可能优于传统的排序算法。

总体评价:

  • 优势: 跳表提供了一种在有序数据集合中实现高效的动态操作的方式，相较于平衡树结构实现较为简单，适用于需要频繁更新和搜索的场景。
  • 劣势: 跳表相对于其他数据结构可能占用更多内存，对于某些内存敏感的场景，可能不是最优选择。在一些特定的搜索密集型场景中，红黑树等平衡树结构也具有竞争力。

总体而言，跳表在一些动态、搜索密集的应用场景中表现出色，但在具体选择时，需要综合考虑数据分布、内存使用、实现难度等因素。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1401848.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Django 图片上传与下载

Django 图片上传与下载

写在前面 在Web开发中&#xff0c;文件上传和下载是常见的功能之一。 Django 是一位魔法师&#x1fa84;&#xff0c;为我们提供了 FileField 和 ImageField 等神奇得字段类型&#xff0c;以及相应的视图和模板标签&#xff0c;使得处理文件变得十分便捷。本文以图片上传作为…
阅读更多...
HTML CSS 发光字头特效

HTML CSS 发光字头特效

效果展示&#xff1a; 代码&#xff1a; <html><head> </head><style>*{margin: 0;padding: 0;}body {text-align: center;}h1{/* border: 3px solid rgb(201, 201, 201); */margin-bottom: 20px;}.hcqFont {position: relative;letter-spacing: 0.07…
阅读更多...
深度解析Python关键字：掌握核心语法的基石(新版本35+4)

深度解析Python关键字：掌握核心语法的基石(新版本35+4)

目录 关键字 keyword 关键字列表 kwlist softkwlist 关键字分类 数据类型 True、False None 运算类型 and、or、not in is 模块导入 import 辅助关键字 from、as 上下文管理 with 占位语句 pass 流程控制 if、elif、else for while break、continue…
阅读更多...
【C语言】动态内存函数介绍

【C语言】动态内存函数介绍

目录 1.malloc和free 2.calloc 3.realloc 1.malloc和free C语言提供了一个动态内存开辟的函数malloc&#xff1a; void* malloc(size_t size); 这个函数向内存申请一块连续可用的空间&#xff0c;并返回指向这块空间的指针。 ✔如果开辟成功&#xff0c;则返回一个指向开…
阅读更多...
数据分析实战：城市房价分析

数据分析实战：城市房价分析

流程图&#xff1a; 1.读数据表 首先&#xff0c;读取数据集。 CRIMZNINDUSCHASNOXRMAGEDISRADTAXPTRATIOBLSTATtarget0.00632182.3100.5386.57565.24.09129615.3396.94.98240.0273107.0700.4696.42178.94.9671224217.8396.99.1421.60.0272907.0700.4697.18561.14.9671224217…
阅读更多...
Python-import hook机制原理与使用

Python-import hook机制原理与使用

背景 钩子函数&#xff08;hook function&#xff09;&#xff0c;可以理解是一个挂钩&#xff0c;作用是有需要的时候挂一个东西上去。具体的解释是&#xff1a;钩子函数是把我们自己实现的hook函数在某一时刻挂接到目标挂载点上。 在 Python 众多特性中&#xff0c;有一个特…
阅读更多...
【设计模式】代理模式的实现方式与使用场景

【设计模式】代理模式的实现方式与使用场景

1. 概述 代理模式是一种结构型设计模式&#xff0c;它通过创建一个代理对象来控制对另一个对象的访问&#xff0c;代理对象在客户端和目标对象之间充当了中介的角色&#xff0c;客户端不再直接访问目标对象&#xff0c;而是通过代理对象间接访问目标对象。 那在中间加一层代理…
阅读更多...
大模型学习与实践笔记（十一）

大模型学习与实践笔记（十一）

一、使用OpenCompass 对模型进行测评 1.环境安装&#xff1a; git clone https://github.com/open-compass/opencompass cd opencompass pip install -e . 当github超时无法访问时&#xff0c;可以在原命令基础上加上地址&#xff1a; https://mirror.ghproxy.com git clon…
阅读更多...
UG制图-创建图纸的多种方法

UG制图-创建图纸的多种方法

1、2D&#xff1a;创建独立2D图纸&#xff0c;不引用任何3D模型 在UG软件中选择新建&#xff0c;或者快捷键ctrl N&#xff0c;进入新建命令&#xff0c;然后点击图纸&#xff0c;在关系中选择独立的部件&#xff0c;就创建了一个独立的图纸&#xff0c;我们可以在装配中添加…
阅读更多...
java eazyexcel 实现excel的动态多级联动下拉列表（1）使用名称管理器+INDIRECT函数

java eazyexcel 实现excel的动态多级联动下拉列表（1）使用名称管理器+INDIRECT函数

原理 将数据源放到一个新建的隐藏的sheet中将选项的子选项的对应字典设置到名称管理器中&#xff08;名称是当前选项的内容&#xff0c;值是他对应的子菜单的单元格范围&#xff0c;在1里面的sheet中&#xff09;子菜单的数据根据INDIRECT函数去左边那个单元格获取内容&#x…
阅读更多...
KMP 算法详解（C++ Version）

KMP 算法详解（C++ Version）

KMP 算法详解&#xff08;C Version&#xff09; 简述字符串匹配问题Brute-Force 算法Brute-Force 算法的改进思路跳过不可能成功的字符串比较next 数组利用 next 数组进行匹配快速求 next 数组 简述 KMP 算法是一种字符串匹配算法&#xff0c;可以在 O(nm) 的时间复杂度内实现…
阅读更多...
ZYNQ程序固化

ZYNQ程序固化

文章目录 一、简介二、固化操作2.1 生成固化文件2.2 固化到SD卡2.3 固化到Flash 参考 将程序存储在非易失性存储器中&#xff0c;在上电或者复位时让程序自动加载运行。 这个过程需要启动引导程序( Boot Loader)参与&#xff0c;Boot Loader会加载FPGA配置文件&#xff0c;以及…
阅读更多...
读元宇宙改变一切笔记12_元宇宙+

读元宇宙改变一切笔记12_元宇宙+

1. 元宇宙的价值 1.1. 元宇宙的价值&#xff0c;将“超过”物理世界 1.2. 移动互联网时代不是突然降临的 1.2.1. 我们可以确定一项特定的技术是何时被创造、测试或部署的&#xff0c;但不能确定一个时代何时开始或何时结束 1.2.2. 转型是一个迭代的过程&#xff0c;在这个过…
阅读更多...
web架构师编辑器内容-完成属性设置的优化

web架构师编辑器内容-完成属性设置的优化

对于业务组件来说&#xff0c;其属性是有很多的&#xff0c;如果把所有属性都平铺在页面上&#xff0c;就会非常长&#xff0c;而且想要更改其中的某些属性&#xff0c;可能需要向下滚动很久才能找到&#xff0c;对于UI的交互不是很友好&#xff0c;需要对属性的不同特性进行分…
阅读更多...
彩色图像处理之彩色图像直方图处理的python实现——数字图像处理

彩色图像处理之彩色图像直方图处理的python实现——数字图像处理

彩色图像的直方图处理是一种重要的图像处理技术&#xff0c;用于改善图像的视觉效果&#xff0c;增强图像的对比度&#xff0c;或为后续的图像处理任务&#xff08;如图像分割、特征提取&#xff09;做准备。彩色图像通常由红色&#xff08;R&#xff09;、绿色&#xff08;G&a…
阅读更多...
2023年12月 Scratch 图形化（一级）真题解析#中国电子学会#全国青少年软件编程等级考试

2023年12月 Scratch 图形化（一级）真题解析#中国电子学会#全国青少年软件编程等级考试

Scratch图形化等级考试（1~4级）全部真题・点这里 一、单选题（共25题，每题2分，共50分） 第1题 观察下列每个圆形中的四个数，找出规律，在括号里填上适当的数？（ ） A：9 B：17 C：21 D：5 答案：C 左上角的数=下面两个数的和+右上角的数
阅读更多...
【UEFI基础】EDK网络框架（UDP4）

【UEFI基础】EDK网络框架（UDP4）

UDP4 UDP4协议说明 UDP的全称是User Datagram Protocol&#xff0c;它不提供复杂的控制机制&#xff0c;仅利用IP提供面向无连接的通信服务。它将上层应用程序发来的数据在收到的那一刻&#xff0c;立即按照原样发送到网络。 UDP报文格式&#xff1a; 各个参数说明如下&…
阅读更多...
Tomcat Notes: Web Security

Tomcat Notes: Web Security

This is a personal study notes of Apache Tomcat. Below are main reference material. - YouTube Apache Tomcat Full Tutorial&#xff0c;owed by Alpha Brains Courses. https://www.youtube.com/watch?vrElJIPRw5iM&t801s 1、Overview2、Two Levels Of Web Securi…
阅读更多...
跨部门算法迭代需求，从提出到上线的全流程实践

跨部门算法迭代需求，从提出到上线的全流程实践

文章目录 引言需求评审技术方案评审模块开发系统联调QA测试产品验收经验教训 引言 最近工作中有一个算法迭代的需求&#xff0c;我在其中作为技术侧负责人&#xff08;技术主R&#xff09;推动需求完成上线。 需求涉及多个部门&#xff0c;前后耗时接近1个月。 我第一次在这…
阅读更多...
transdata笔记：手机数据处理

transdata笔记：手机数据处理

1 mobile_stay_duration 每个停留点白天和夜间的持续时间 transbigdata.mobile_stay_duration(staydata, col[stime, etime], start_hour8, end_hour20) 1.1 主要参数 staydata停留数据&#xff08;每一行是一条数据&#xff09;col 列名&#xff0c;顺序为[‘starttime’,…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023