简述

KMP 算法是一种字符串匹配算法，可以在 O(n+m) 的时间复杂度内实现两个字符串的匹配。

字符串匹配问题

所谓字符串匹配，是这样一种问题：字符串 P 是否为字符串 S 的子串？如果是，它出现在 S 的哪些位置？”

其中 S 称为主串；P 称为模式串。下面的图片展示了一个例子。

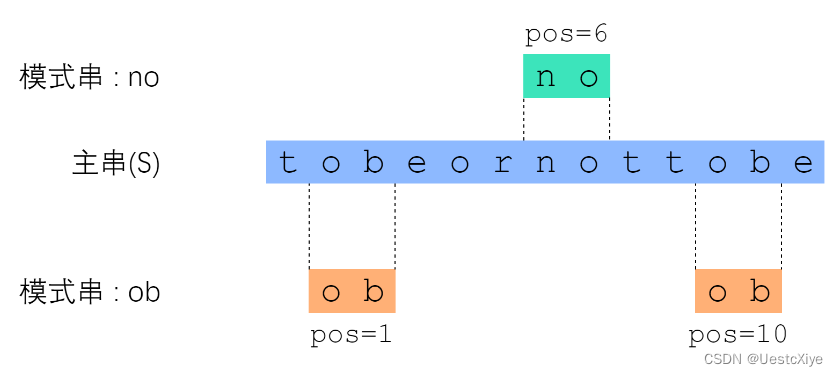
主串是莎翁那句著名的 “to be or not to be”，这里删去了空格。

“no” 这个模式串的匹配结果是：“出现了一次，从 S[6] 开始”；

“ob” 这个模式串的匹配结果是“出现了两次，分别从s[1]、s[10]开始”。

按惯例，主串和模式串都以 0 开始编号。

Brute-Force 算法

字符串匹配是一个非常频繁的任务。例如，今有一份名单，你急切地想知道自己在不在名单上；又如，假设你拿到了一份文献，你希望快速地找到某个关键字（keyword）所在的章节……凡此种种，不胜枚举。

我们先从最朴素的Brute-Force算法开始讲起。

顾名思义，Brute-Force 是一个纯暴力算法。

首先，我们应该如何实现两个字符串 s1、s2 的比较？

所谓字符串比较，就是问“两个字符串是否相等”。

最朴素的思想，就是从前往后逐字符比较，一旦遇到不相同的字符，就返回 false；如果两个字符串都结束了，仍然没有出现不对应的字符，则返回 true。

实现如下：

bool is_equal(string &s1, string &s2)
{
	if (s1.length() != s2.length())
		return false;

	for (int i = 0; i < s1.length(); i++)
		if (s1[i] != s2[i])
			return false;
	return true;
}

既然我们可以知道“两个字符串是否相等”，那么最朴素的字符串匹配算法 Brute-Force 就呼之欲出了：

1. 枚举比较的起点 i = 0, 1, 2 … , len(s) - len(pattern)；
2. 将 s[i : i+len(pattern)] 与 pattern 作比较。如果一致，则找到了一个匹配。

现在我们来模拟 Brute-Force 算法，对主串 “AAAAAABC” 和模式串 “AAAB” 做匹配：

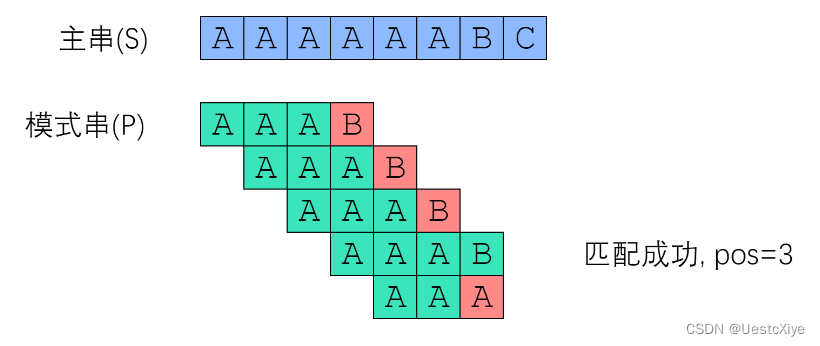
现在给出 Brute-Force 算法的实现：

vector<int> bruteForce(string &s, string &pattern)
{
	int slen = s.length(), plen = pattern.length();
	vector<int> res;
	for (int i = 0; i <= slen - plen; i++)
	{
		string tmp = s.substr(i, plen);
		if (is_equal(tmp, pattern))
			res.push_back(i);
	}
	return res;
}

我们成功实现了 Brute-Force 算法。现在，我们需要对它的时间复杂度做一点讨论。

按照惯例，记 n = len(s) 为字符串 s 的长度，m = len(pattern) 为模式串 pattern 的长度。

不难想到 Brute-Force 算法所面对的最坏情况：主串形如 “AAAAAAAAAAA…B”，而模式串形如 “AAAAA…B”。

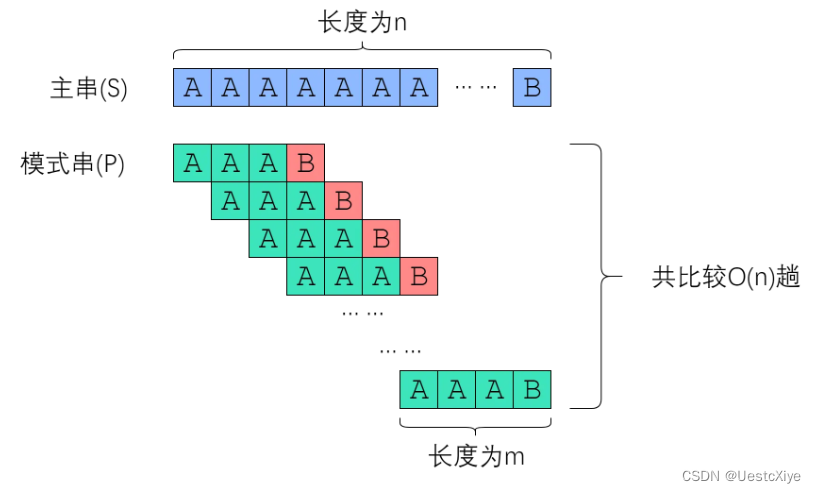
每次字符串比较都需要付出 len(pattern) 次字符比较的代价，总共需要比较 len(s) - len(pattern) + 1次，因此总时间复杂度是 O(len(pattern) * (len(s) - len(pattern) + 1))，考虑到主串一般比模式串长很多，故 Brute-Force 的复杂度是 O(len(pattern) * len(s))，也就是 O(mn)，这太慢了！

Brute-Force 算法的改进思路

我们很难降低字符串比较的复杂度（因为比较两个字符串，真的只能逐个比较字符）。因此，我们考虑降低比较的趟数。

如果比较的趟数能降到足够低，那么总的复杂度也将会下降很多。

在 Brute-Force 算法中，如果从 s[i] 开始的那一趟比较失败了，算法会直接开始尝试从 s[i+1] 开始比较。这种行为，属于典型的 “没有从之前的错误中学到东西”。我们应当注意到，一次失败的匹配，会给我们提供宝贵的信息——如果 s[i : i+len(pattern)] 与 pattern 的匹配是在第 r 个位置失败的，那么从 s[i] 开始的 (r-1) 个连续字符，一定与 pattern 的前 (r-1) 个字符一模一样！

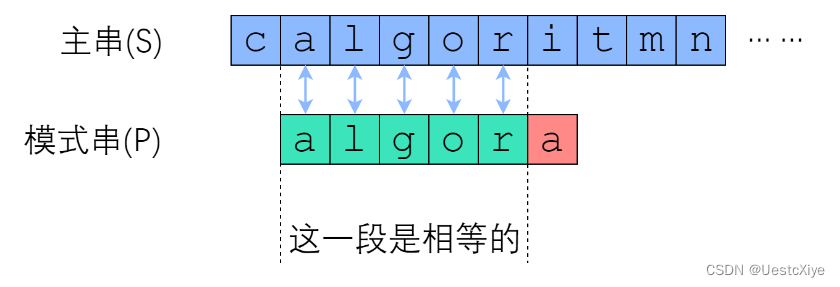
需要实现的任务是“字符串匹配”，而每一次失败都会给我们换来一些信息——主串的某一个子串等于模式串的某一个前缀。

但是这又有什么用呢？

跳过不可能成功的字符串比较

有些趟字符串比较是有可能会成功的；有些则毫无可能。

我们刚刚提到过，优化 Brute-Force 算法的思路是 “尽量减少比较的趟数”，而如果我们跳过那些绝不可能成功的字符串比较，则可以希望复杂度降低到能接受的范围。

那么，哪些字符串比较是不可能成功的？

来看一个例子。已知信息如下：

• 模式串 pattern = “abcabd”。
• 和主串从 s[0] 开始匹配时，在 pattern[5] 处失配。

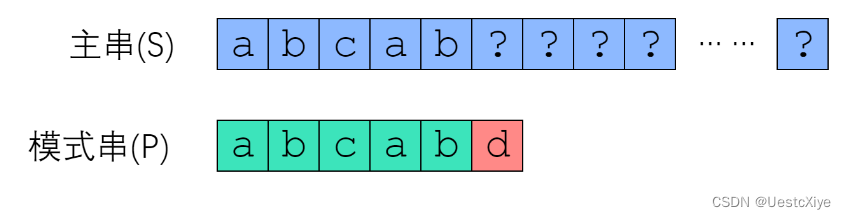
首先，利用上一节的结论，既然是在 pattern[5] 失配的，那么说明 s[0:5] 等于 pattern[0:5]，即 “abcab”。

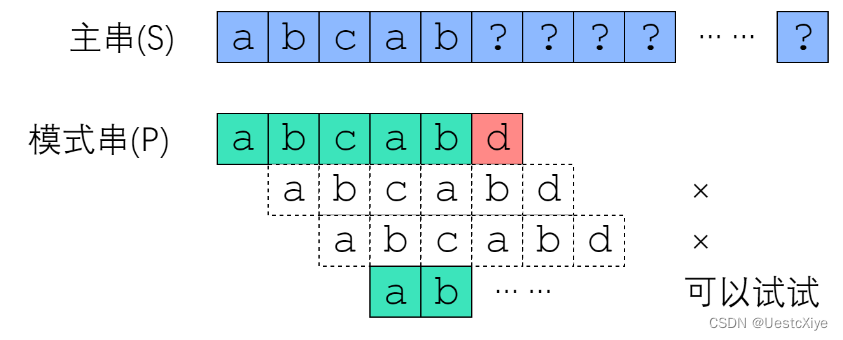
现在我们来考虑：从 s[1]、s[2]、s[3] 开始的匹配尝试，有没有可能成功？

从 s[1] 开始肯定没办法成功，因为 s[1] = pattern[1] = ‘b’，和 pattern[0] 并不相等。

从 s[2] 开始也是没戏的，因为 s[2] = pattern[2] = ‘c’，并不等于 pattern[0]。

但是从 s[3] 开始是有可能成功的——至少按照已知的信息，我们推不出矛盾。

带着“跳过不可能成功的尝试”的思想，我们来看 next 数组。

next 数组

next 数组是对于模式串 pattern 而言的。

pattern 的 next 数组定义为：next[i] 表示 pattern[0] ~ pattern[i] 这一个子串，使得前 k 个字符恰等于后 k 个字符的最大的 k。特别地，k 不能取 i+1（因为这个子串一共才 i+1 个字符，自己肯定与自己相等，就没有意义了）。

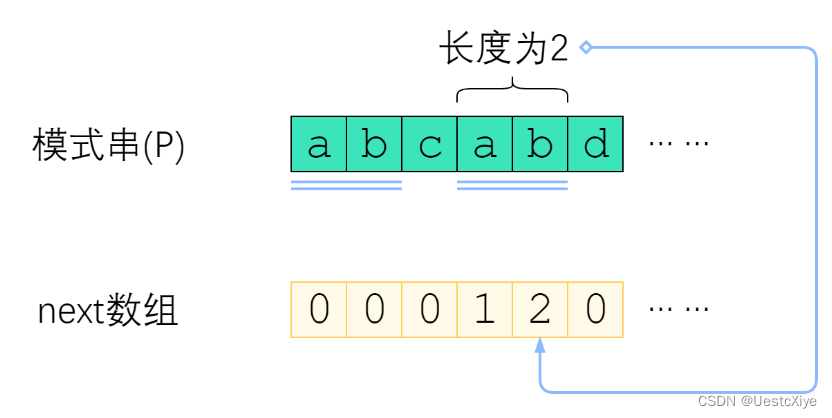
上图给出了一个例子。pattern=“abcabd” 时，next[4]=2，这是因为 pattern[0:4] 这个子串是 “abcab”，前两个字符与后两个字符相等，因此 next[4]=2；而 next[5]=0，是因为 “abcabd” 找不到前缀与后缀相同，因此只能取 0。

如果把模式串视为一把标尺，在主串上移动，那么 Brute-Force 算法就是每次失配之后只右移一位；改进算法则是每次失配之后，移很多位，跳过那些不可能匹配成功的位置。但是该如何确定要移多少位呢？

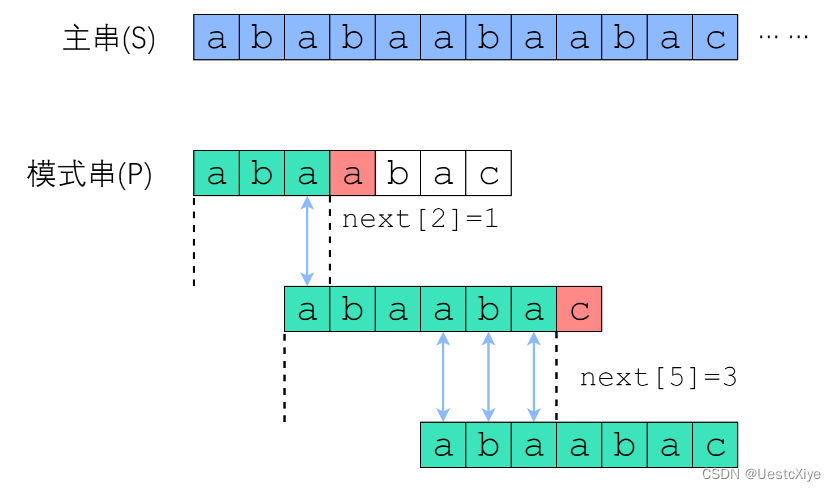
在 s[0] 尝试匹配，失配于 s[3] <=> pattern[3] 之后，我们直接把模式串往右移了两位，让 s[3] 对准 pattern[1]。

接着继续匹配，失配于 s[8] <=> pattern[6], 接下来我们把 pattern 往右平移了三位，把 s[8] 对准 pattern[3]。

此后继续匹配直到成功。

我们应该如何移动这把标尺？很明显，如图中蓝色箭头所示，旧的后缀要与新的前缀一致。如果不一致，那就肯定没法匹配上了！

回忆 next 数组的性质：pattern[0] 到 pattern[i] 这一段子串中，前 next[i] 个字符与后 next[i] 个字符一模一样。既然如此，如果失配在 pattern[r], 那么 pattern[0:r-1] 这一段里面，前 next[r-1] 个字符恰好和后 next[r-1] 个字符相等——也就是说，我们可以拿长度为 next[r-1] 的那一段前缀，来顶替当前后缀的位置，让匹配继续下去！

验证一下上面的匹配例子：pattern[3] 失配后，把 pattern[next[3-1]] 也就是 pattern[1] 对准了主串刚刚失配的那一位；pattern[6] 失配后，把 pattern[next[6-1]] 也就是 pattern[3] 对准了主串刚刚失配的那一位。

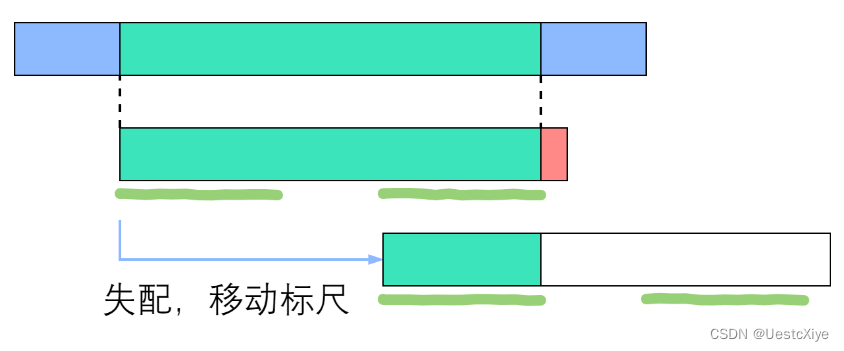
如上图所示，绿色部分是成功匹配，失配于红色部分。深绿色手绘线条标出了相等的前缀和后缀，其长度为 next[右端]。由于手绘线条部分的字符是一样的，所以直接把前面那条移到后面那条的位置。因此说，next 数组为我们如何移动标尺提供了依据。接下来，我们实现这个优化的算法。

利用 next 数组进行匹配

了解了利用next数组加速字符串匹配的原理，我们接下来用代码实现。

分为两个部分：

1. 建立 next 数组。
2. 利用 next 数组进行匹配。

首先是建立 next 数组。我们暂且用最朴素的做法，以后再回来优化：

vector<int> getNxt(string &pattern)
{
	int m = pattern.length();
	vector<int> nxt(m, 0);
	for (int i = 0; i < m; i++)
	{
		string sub = pattern.substr(0, i + 1);
		for (int j = sub.length() - 1; j >= 0; j--)
		{
			string prev = sub.substr(0, j);
			string suf = sub.substr(sub.length() - j, j);
			if (prev == suf)
			{
				nxt[i] = j;
				break;
			}
		}
	}
	return nxt;
}

计 m = len(pattern) 为模式串 pattern 的长度，不难发现它的时间复杂度是 O(m²)。

接下来，实现利用 next 数组加速字符串匹配。代码如下：

vector<int> kmp(string &s, string &pattern)
{
	int m = pattern.length();
	vector<int> nxt = getNxt(pattern);
	vector<int> res;
	int tar = 0; // 主串中将要匹配的位置
	int pos = 0; // 模式串中将要匹配的位置
	while (tar < s.length())
	{
		if (s[tar] == pattern[pos])
		{
			// 若两个字符相等，则 tar、pos 各进一步
			tar++;
			pos++;
		}
		else if (pos != 0)
		{
			// 失配，如果 pos != 0，则依据 nxt 移动标尺
			pos = nxt[pos - 1];
		}
		else
		{
			// pos[0] 失配，标尺右移一位
			tar++;
		}

		if (pos == pattern.length())
		{
			res.push_back(tar - pos);
			pos = nxt[pos - 1];
		}
	}
	return res;
}

如何分析这个字符串匹配的复杂度呢？按照惯例，记 n = len(s) 为字符串 s 的长度，m = len(pattern) 为模式串 pattern 的长度。

乍一看，pos 值可能不停地变成 next[pos-1]，代价会很高；但显然pos值一共顶多自增 len(s) 次，因此 pos 值减少的次数不会高于 len(s) 次。由此，复杂度是可以接受的，不难分析出整个匹配算法的时间复杂度：O(n+m)。

快速求 next 数组

终于来到了我们最后一个问题——如何快速构建 next 数组。

首先说一句：快速构建 next 数组，是 KMP 算法的精髓所在，核心思想是 “pattern 自己与自己做匹配”。

为什么这样说呢？回顾 next 数组的完整定义：定义 “k-前缀” 为一个字符串的前 k 个字符； “k-后缀” 为一个字符串的后 k 个字符。k 必须小于字符串长度。 next[x] 定义为： pattern[0:x] 这一段字符串，使得 “k-前缀” 恰等于 “k-后缀” 的最大的 k。这个定义中，不知不觉地就包含了一个匹配——前缀和后缀相等。

接下来，我们考虑采用递推的方式求出 next 数组。如果next[0], next[1], … next[x-1] 均已知，那么如何求出 next[x] 呢？

来分情况讨论。首先，已经知道了 next[x-1]（以下记为 now），如果 pattern[x] 与 pattern[now] 一样，那最长相等前后缀的长度就可以扩展一位，即 next[x] = now + 1。图示如下：

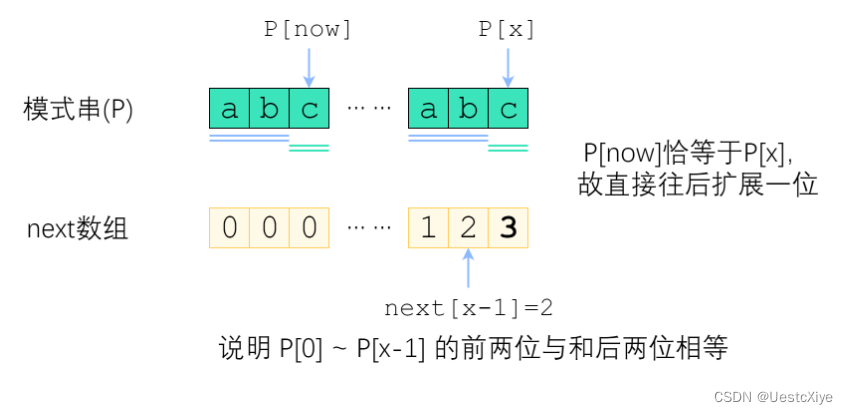
刚刚解决了 pattern[x] = pattern[now] 的情况。那如果 pattern[x] 与 pattern[now] 不一样，又该怎么办？

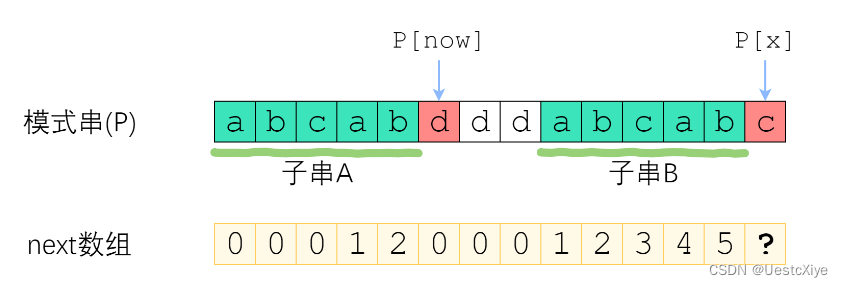
如上图，长度为 now 的子串 A 和子串 B 是 pattern[0:x-1] 中最长的公共前后缀。可惜 A 右边的字符和 B 右边的那个字符不相等，next[x] 不能改成 now+1 了。

因此，我们应该缩短这个now，把它改成小一点的值，再来试试 pattern[x] 是否等于 pattern[now]。

now 该缩小到多少呢？显然，我们不想让 now 缩小太多。因此我们决定，在保持 “pattern[0:x-1] 的 now-前缀 仍然等于 now-后缀” 的前提下，让这个新的 now 尽可能大一点。 pattern[0:x-1] 的公共前后缀，前缀一定落在串 A 里面、后缀一定落在串 B 里面。换句话讲：接下来 now 应该改成：使得 A 的 “k-前缀” 等于 B 的 “k-后缀” 的最大的 k。你应该已经注意到了一个非常强的性质——串 A 和串 B 是相同的！B 的后缀等于 A 的后缀！因此，使得 A 的 “k-前缀” 等于B的 “k-后缀” 的最大的 k，其实就是串 A 的最长公共前后缀的长度 —— next[now-1]！

来看上面的例子。当 pattern[now] 与 pattern[x] 不相等的时候，我们需要缩小 now——把 now 变成 next[now-1]，直到 pattern[now]=pattern[x] 为止。

pattern[now]=pattern[x] 时，就可以直接向右扩展了。

代码实现如下：

vector<int> getNxt(string &pattern)
{
	vector<int> nxt;
	// next[0] 必然是 0
	nxt.push_back(0);
	// 从 next[1] 开始求
	int x = 1, now = 0;
	while (x < pattern.length())
	{
		if (pattern[now] == pattern[x])
		{
			// 如果 pattern[now] == pattern[x]，向右拓展一位
			now++;
			x++;
			nxt.push_back(now);
		}
		else if (now != 0)
		{
			// 缩小 now，改成 nxt[now - 1]
			now = nxt[now - 1];
		}
		else
		{
			// now 已经为 0，无法再缩小，故 next[x] = 0
			nxt.push_back(0);
			x++;
		}
	}
	return nxt;
}

不难证明构建 next 数组的时间复杂度是 O(m) 的。至此，我们以 O(n+m) 的时间复杂度，实现了构建 next 数组、利用 next 数组进行字符串匹配。

以上就是 KMP 算法。它于 1977 年被提出，全称 Knuth–Morris–Pratt 算法。让我们记住前辈们的名字：Donald Knuth(K)，James H. Morris(M)，Vaughan Pratt(P)。

最后给出完整模板：

vector<int> getNxt(string &pattern)
{
	vector<int> nxt;
	// next[0] 必然是 0
	nxt.push_back(0);
	// 从 next[1] 开始求
	int x = 1, now = 0;
	while (x < pattern.length())
	{
		if (pattern[now] == pattern[x])
		{
			// 如果 pattern[now] == pattern[x]，向右拓展一位
			now++;
			x++;
			nxt.push_back(now);
		}
		else if (now != 0)
		{
			// 缩小 now，改成 nxt[now - 1]
			now = nxt[now - 1];
		}
		else
		{
			// now 已经为 0，无法再缩小，故 next[x] = 0
			nxt.push_back(0);
			x++;
		}
	}
	return nxt;
}

vector<int> kmp(string &s, string &pattern)
{
	int m = pattern.length();
	vector<int> nxt = getNxt(pattern);
	vector<int> res;
	int tar = 0; // 主串中将要匹配的位置
	int pos = 0; // 模式串中将要匹配的位置
	while (tar < s.length())
	{
		if (s[tar] == pattern[pos])
		{
			// 若两个字符相等，则 tar、pos 各进一步
			tar++;
			pos++;
		}
		else if (pos != 0)
		{
			// 失配，如果 pos != 0，则依据 nxt 移动标尺
			pos = nxt[pos - 1];
		}
		else
		{
			// pos[0] 失配，标尺右移一位
			tar++;
		}

		if (pos == pattern.length())
		{
			res.push_back(tar - pos);
			pos = nxt[pos - 1];
		}
	}
	return res;
}