一、介绍
Allan方差是一种分析时域数据序列的方法,用于测量振荡器的频率稳定性。该方法还可用于确定系统中作为平均时间函数的本征噪声。该方法易于计算和理解,是目前最流行的识别和量化惯性传感器数据中存在的不同噪声项的方法之一。该方法的结果与适用于惯性传感器数据的五个基本噪声项有关。这些是量化噪声、角度随机游走、偏置不稳定性、速率随机游走和速率斜坡。
时域信号Ω(𝑡)的Allan方差分析是计算其根Allan方差或Allan偏差作为不同平均次数的函数,然后分析Allan偏差曲线的特征区域和对数曲线,以识别不同的噪声模式。
二、建立用于陀螺仪噪声识别的Allan偏差图
下面描述了创建Allan偏差图所需遵循的步骤。本文采用重叠Allan方差法计算Allan方差并生成Allan偏差图进行噪声分析。
步骤如下:
- 使用实验装置获取陀螺仪输出的时间序列Ω(𝑡)(保持陀螺仪静态)。设样本个数为N,采样周期为 τ 0 τ_0 τ0。
- 设置平均时间为: τ = m τ 0 τ=mτ_0 τ=mτ0,m为平均因子。𝑚的值可以任意选择,并且保证𝑚<(N- 1)/2。
- 将信号的时间序列(即陀螺输出数据随时间的序列)划分为时间长度为
τ
=
m
τ
0
τ=mτ_0
τ=mτ0的有限集合。
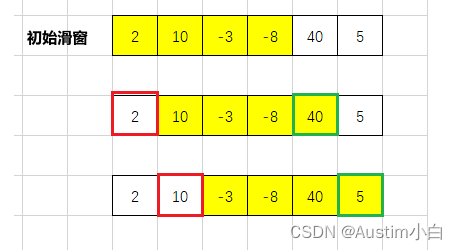
在这种重叠Allan方差方法中,两个连续数据集合之间的时间跨度始终等于样本周期𝜏0。这种重叠方法利用平均时间来形成所有可能重叠的样本集合,最大限度地利用了数据集。如下图所示。
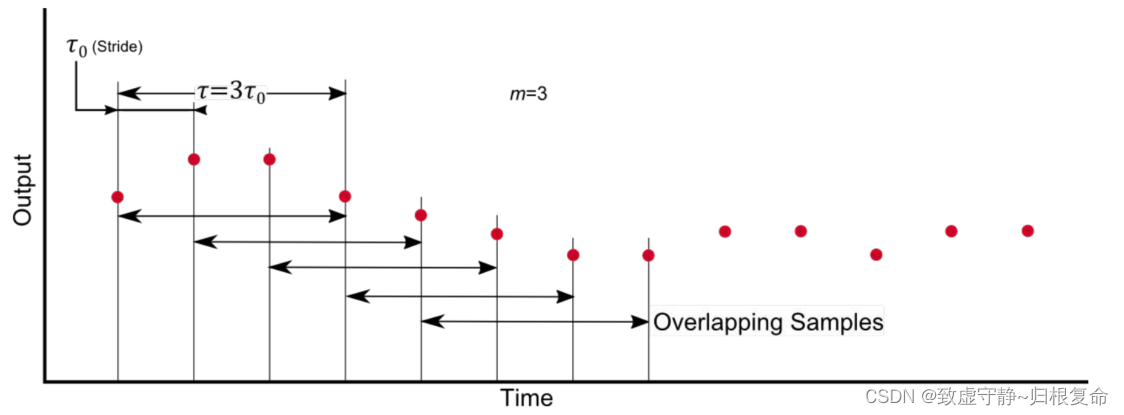
如上图所示为平均因子𝑚= 3的重叠方法的样本集合。两个相邻集合具有重叠的样本。每个集合关联的持续时间为3个。每个集合之间通过采样周期为𝜏0 (Stride)隔开。 - 一旦集合形成,就可以用两种方法计算Allan方差(通过重叠法):
①使用输出速率样本的平均值,见第2.1节
②输出角θ对应于每个陀螺速率样本,见第2.2节 - 最后,计算该特定值的Allan偏差值,然后对多个值重复上述步骤得到Allan偏差图,见第2.3节。
2.1 使用输出速率样本的平均值计算Allan方差
Allan方差可以根据每个数据集上输出速率样本的平均值来计算。
1. 在
K
τ
0
Kτ_0
Kτ0和
K
τ
0
+
τ
Kτ_0+τ
Kτ0+τ之间对每个数据集的输出速率样本取平均值。
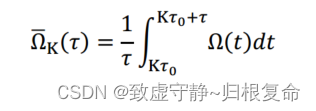
同样,在2.2节“使用输出角计算Allan方差”中会计算了θ的值,使用输出角计算平均输出速率
Ω
ˉ
K
(
τ
)
\bar \Omega_K(τ)
ΩˉK(τ)。在
K
τ
0
Kτ_0
Kτ0和
K
τ
0
+
τ
Kτ_0+τ
Kτ0+τ次之间,以输出角
θ
K
\theta_Κ
θK表示的平均产出率为:
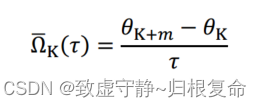
例如:
Ω
ˉ
2
(
τ
)
\bar \Omega_2(τ)
Ωˉ2(τ)和假设𝑚= 3表示平均陀螺的输出之间的集群乘以2𝜏0和2𝜏0+3𝜏0=5𝜏0。这就等于:

通过上面三式,对一个特定的值计算出Ω的所有可能值(在每个数据集上)。由于在这种方法中有𝑚可能形成的数据集,因此计算Ω的值。
Ω的所有可能值(每个簇上)都是已知的,Allan方差可以计算如下:

这是艾伦方差的定义。
δ
2
(
τ
)
\delta^2(τ)
δ2(τ)表示Allan方差是的函数,< >为集合平均值。将上式展开,得到:
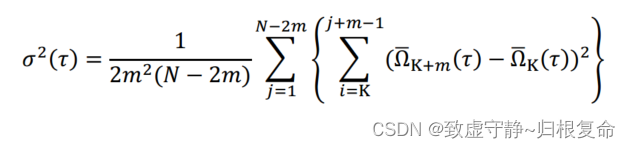
这个方程表示陀螺仪对一个特定值τ的最终速率Allan方差(重叠法),通过使用输出速率值的平均值,
Ω
ˉ
(
τ
)
\bar\Omega(τ)
Ωˉ(τ)在每个数据集上。
2.2 使用输出角度计算Allan方差
Allan方差可以根据输出角θ来计算,对应于每个陀螺速率采样值。
1.计算每个陀螺输出样本对应的θ。这可以通过以下方式计算:
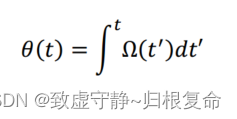
有时这些角度测量是由𝑡𝑡=𝑘𝜏0(𝜏0,2𝜏0,3𝜏0…),𝑘变化从1到𝑁。对于一个离散的样本集,累积和也可以用来给出θ的N值。在这里,取每个𝑘𝜏0上陀螺仪输出样本的累积和,然后将得到的每个和乘以样本周期𝜏0来得到θ的二进制操作值。
示例:计算θ的三个值,假设𝑘在1到3个样本之间变化。
假设观测到的 Ω k \Omega_k Ωk值分别为10、12和15。
通过使用累积和,可以得到以下值:10,10 +12=22和10 + 12 + 15 = 37。
进一步乘以𝜏0,我们现在得到的相应值: θ k : θ 1 = 10 τ 0 , : θ 2 = 22 τ 0 , : θ 3 = 37 τ 0 \theta_k:\theta_1=10τ_0,:\theta_2=22τ_0,:\theta_3=37τ_0 θk:θ1=10τ0,:θ2=22τ0,:θ3=37τ0
2. 一旦计算了θ的N值,使用下式计算Allan方差。

δ
2
(
τ
)
\delta^2(τ)
δ2(τ)表示Allan方差是的函数,< >为集合平均值。将上式展开,得到:
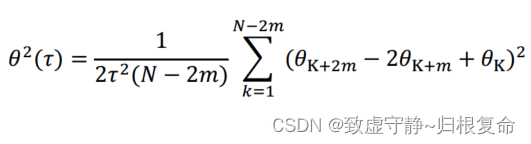
这里的二进制操作是样本总数,𝑚是平均因子,τ=𝑚
τ
0
τ_0
τ0是平均时间,𝐾是一组从1到N的离散值。
上式利用陀螺仪的输出角θ计算出某一特定值下的最终速率Allan方差(通过重叠法)值。一旦我们知道了θ的输出角度值、样本周期和𝑚的值,我们就可以用这个方程来计算Allan方差。
2.3 计算Allan偏差并创建Allan偏差图
最后,对2.1节或2.2节的结果取平方根,就可以得到某一特定值的根Allan方差或Allan偏差的值。这个结果现在将被用来表征陀螺仪中的噪声。
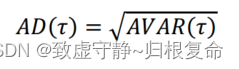
三、噪声识别
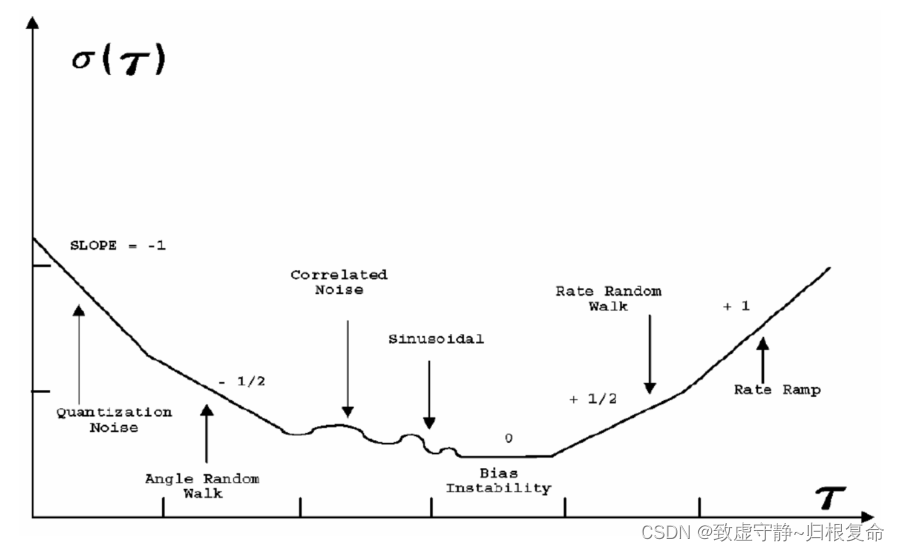
不同类型的随机过程导致Allan偏差图上出现不同梯度的斜率。不同的过程通常出现在不同的区域,使得它们的存在很容易被识别。确定了一个过程之后,就可以直接从绘图中读取其数值参数。对于像陀螺仪这样的MEMS器件,要测量的重要过程是随机游走和偏置不稳定性(有时也称为偏置稳定性),其可以识别和读取如下:
- 白噪声/随机游走:在Allan方差图上显示为梯度为-0.5的斜率。该噪声的随机游走测量(速率陀螺仪的ARW,加速度计的VRW)是通过斜率拟合一条直线并读取其在= 1处的值获得的。陀螺仪的ARW是陀螺仪噪声的度量,单位为dps/rt(Hz)。
- 偏置不稳定性:在图上表现为最小值周围的平坦区域。数值是Allan偏差图上的最小值。对于陀螺仪,偏置稳定性测量陀螺仪的偏置如何在恒定温度下在指定的时间内变化。这通常以dps/秒或dps/小时为单位。
下图显示了从艾伦偏差图中可以观察到的各种不同的噪声过程。从下图中可以看出,陀螺仪需要观察、计算和分析的噪声过程是角度随机游走和偏置不稳定性。
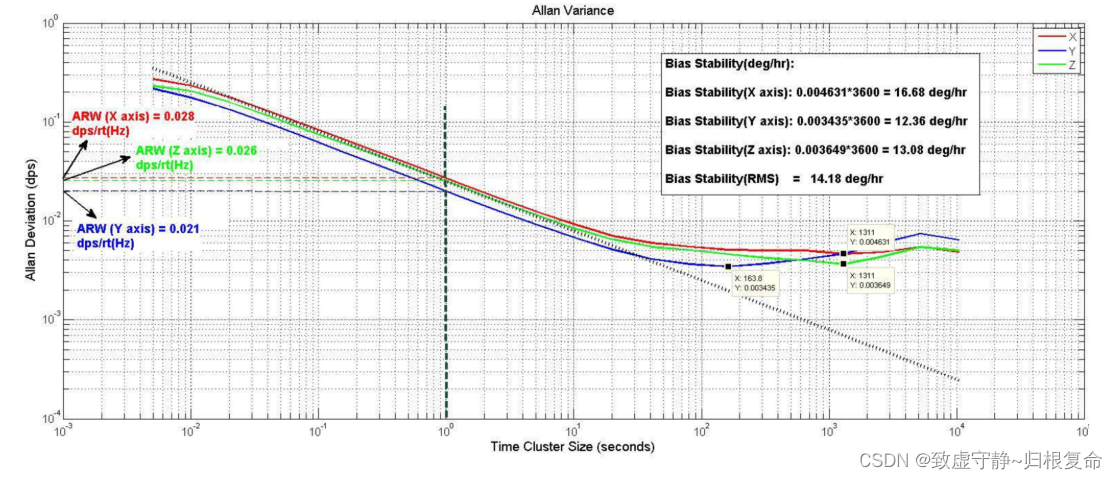
下图显示了飞思卡尔陀螺仪FXAS21002C对应的Allan方差曲线。偏置稳定性和ARW值在下图中有明显的标记。
Allan方差代码:
function [T,sigma] = allan(omega,fs,pts)
[N,M] = size(omega); % figure out how big the output data set is
n = 2.^(0:floor(log2(N/2)))'; % determine largest bin size
maxN = n(end);
endLogInc = log10(maxN);
m = unique(ceil(logspace(0,endLogInc,pts)))'; % create log spaced vector average factor
t0 = 1/fs; % t0 = sample interval
T = m*t0; % T = length of time for each cluster
theta = cumsum(omega)/fs; % integration of samples over time to obtain output angle θ
sigma2 = zeros(length(T),M); % array of dimensions (cluster periods) X (#variables)
for i=1:length(m) % loop over the various cluster sizes
for k=1:N-2*m(i) % implements the summation in the AV equation
sigma2(i,:) = sigma2(i,:) + (theta(k+2*m(i),:) - 2*theta(k+m(i),:) + theta(k,:)).^2;
end
end
sigma2 = sigma2./repmat((2*T.^2.*(N-2*m)),1,M);
sigma = sqrt(sigma2)
代码解释:
- omega是陀螺速率输出。
- m任意选取,τ定义为M *样本周期。
- 在上面的代码中,使用2.2节中描述的方法来计算Allan方差。
- theta由输出速率数据的累积和除以采样频率得到。这个θ是对应于每个样本得到的输出角度。
- 由于m是可用的,每个输出速率样本对应的输出角度也是可用的,因此在上述代码中直接实现式(3)来计算Allan方差(代码中的sigma2)。
- Allan偏差(代码中的sigma)然后通过取AVAR的平方根,即用2.3节公式来计算。
四、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记
课题学习(十一)----阅读《Attitude Determination with Magnetometers and Accelerometers to Use in Satellite》
课题学习(十二)----阅读《Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes》
课题学习(十三)----阅读《Calibration of Strapdown Magnetometers in Magnetic Field Domain》论文笔记
课题学习(十四)----三轴加速度计+三轴陀螺仪传感器-ICM20602
课题学习(十五)----阅读《测斜仪旋转姿态测量信号处理方法》论文
课题学习(十六)----阅读《Continuous Wellbore Surveying While Drilling Utilizing MEMS Gyroscopes Based…》论文
课题学习(十七)----姿态更新的四元数算法总结
课题学习(十八)----捷联测试电路设计与代码实现(基于MPU6050和QMC5883L)