Improving the Beginner’s PID
参考资料
Improving the Beginner’s PID – Introduction
The Beginner’s PID
以下是每个人第一次学习的PID方程:
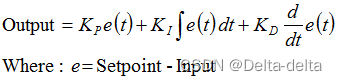
这导致几乎每个人都编写了以下PID控制器:
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
void Compute()
{
/*How long since we last calculated*/
unsigned long now = millis();
double timeChange = (double)(now - lastTime);
/*Compute all the working error variables*/
double error = Setpoint - Input;
errSum += (error * timeChange);
double dErr = (error - lastErr) / timeChange;
/*Compute PID Output*/
Output = kp * error + ki * errSum + kd * dErr;
/*Remember some variables for next time*/
lastErr = error;
lastTime = now;
}
void SetTunings(double Kp, double Ki, double Kd)
{
kp = Kp;
ki = Ki;
kd = Kd;
}
Compute()可以定期调用,也可以不定期调用,而且它运行得很好。不过,这个系列并不是关于“效果很好”的。如果我们要将此代码转化为与工业PID控制器相当的代码,我们必须解决以下几点:
-
Sample Time
如果以规则的间隔对PID算法进行评估,则PID算法的功能最佳。如果算法知道这个区间,我们也可以简化一些内部数学。 -
Derivative Kick
这不是最大的交易,但很容易摆脱,所以我们将这么做。 -
On-The-Fly Tuning Changes
一个好的PID算法是可以在不影响内部工作的情况下更改调整参数的算法。 -
Reset Windup Mitigation
我们将深入了解什么是Reset Windup,并实施一个具有副作用的解决方案 -
On/Off (Auto/Manual)
在大多数应用中,有时需要关闭PID控制器并手动调整输出,而不会受到控制器的干扰. -
Initialization
当控制器第一次打开时,我们想要一个“无颠簸的传输”。也就是说,我们不希望输出突然急动到某个新值。 -
Controller Direction
最后一个并不是健壮性本身的名称的改变。它旨在确保用户输入的调整参数具有正确的符号。 -
NEW: Proportional on Measurement
添加此功能可以更容易地控制某些类型的进程。
Improving the Beginner’s PID – Sample Time
初学者PID被设计为不规则调用。这导致2个问题:
- 您无法从PID获得一致的行为,因为有时它被频繁调用,有时它不被调用。
- 你需要做额外的数学计算导数和积分,因为它们都取决于时间的变化。
确保定期调用PID。我决定这样做的方式是指定在每个周期调用计算函数。PID根据预先确定的采样时间决定是否应该立即计算或返回。
一旦我们知道PID以恒定的间隔进行评估,导数和积分计算也可以简化。

在第10行和第11行,算法现在自行决定是否该进行计算。此外,因为我们现在知道样本之间的时间是相同的,所以我们不需要不断地乘以时间变化。我们只能适当地调整Ki和Kd(第31和32行),结果在数学上是等效的,但更有效。
不过,这样做有点麻烦。如果用户决定在操作期间更改采样时间,则Ki和Kd将需要重新调整以反映这一新变化。这就是第39-42行的全部内容。
另外请注意,我在第29行将采样时间转换为秒。严格来说,这是不必要的,但允许用户以1秒和s为单位输入Ki和Kd,而不是以1/mS和mS为单位。
上面的变化为我们做了3件事
- 无论调用Compute()的频率有多高,PID算法都将以一定的间隔进行评估[第11行]
- 由于时间相减[第10行],当millis()返回到0时不会出现问题。这种情况每55天才会发生一次
- 我们再也不需要用时间变化来乘和除了。由于它是一个常数,我们可以将其从计算代码中移出[第15+16]行],并将其与调整常数[第31+32]行]合并。从数学上讲,它的结果是一样的,但每次评估PID时都会节省一次乘法和除法.
关于中断的旁注:如果这个PID进入微控制器,那么可以为使用中断提供一个很好的论据。SetSampleTime设置中断频率,然后在该时间调用Compute。在这种情况下,不需要第9-12、23和24行。如果你打算用你的PID实现来做这件事,那就去做吧!请继续阅读本系列。希望您仍能从接下来的修改中获得一些好处。
Improving the Beginner’s PID – Derivative Kick
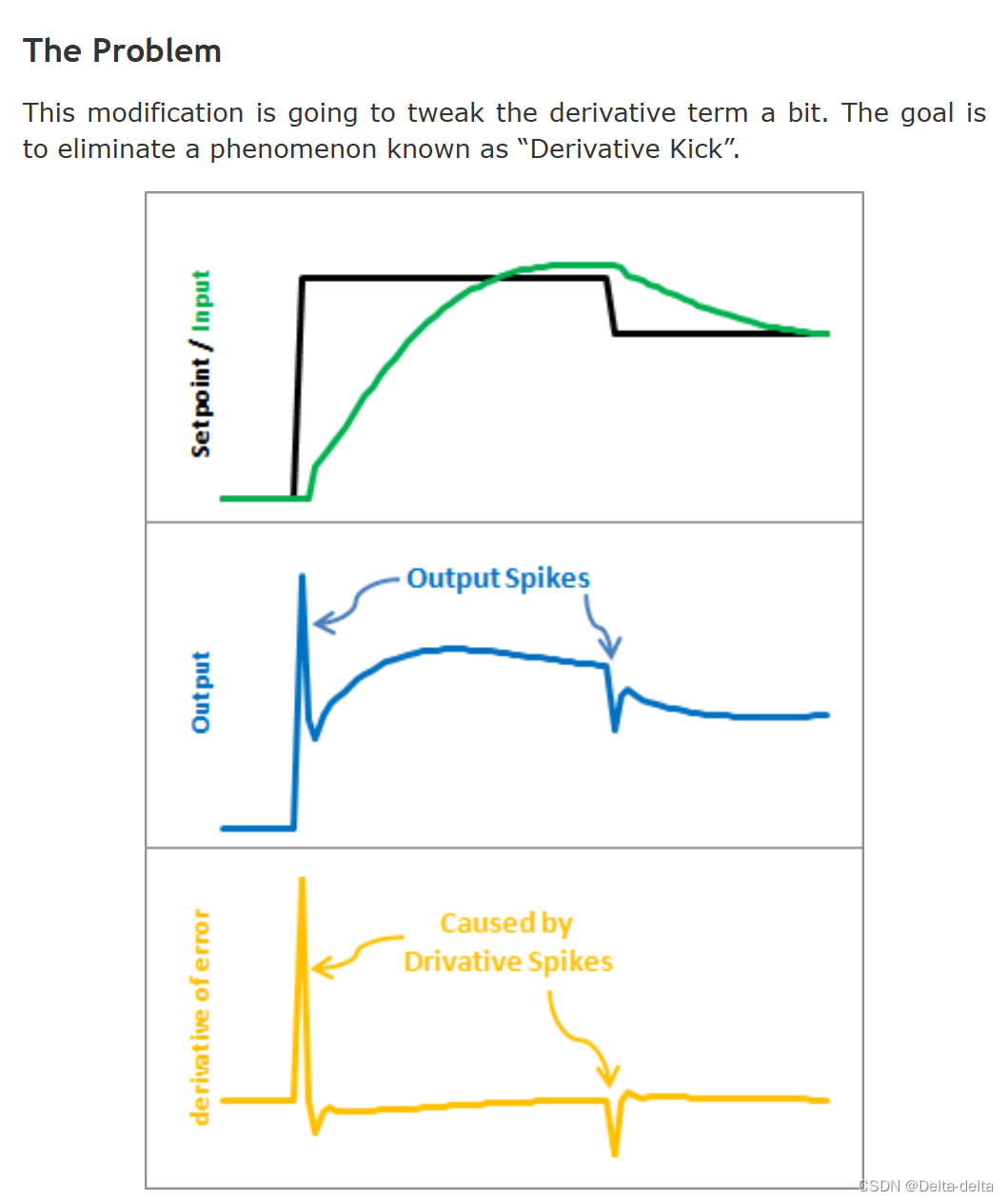
上图说明了这个问题。由于误差=设定点-输入,设定点的任何变化都会导致误差的瞬时变化。这种变化的导数是无穷大的(在实践中,由于dt不是0,它最终会成为一个非常大的数字。)这个数字被输入到pid方程中,这会导致输出出现不希望的峰值。幸运的是,有一种简单的方法可以消除这种情况。

事实证明,误差的导数等于输入的负导数,除非设定值发生变化。这最终成为一个完美的解决方案。我们不加(Kd误差导数),而是减去(KdInput导数)。这被称为使用“测量导数”.
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
errSum += error;
double dInput = (Input - lastInput);
/*Compute PID Output*/
Output = kp * error + ki * errSum - kd * dInput;
/*Remember some variables for next time*/
lastInput = Input;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
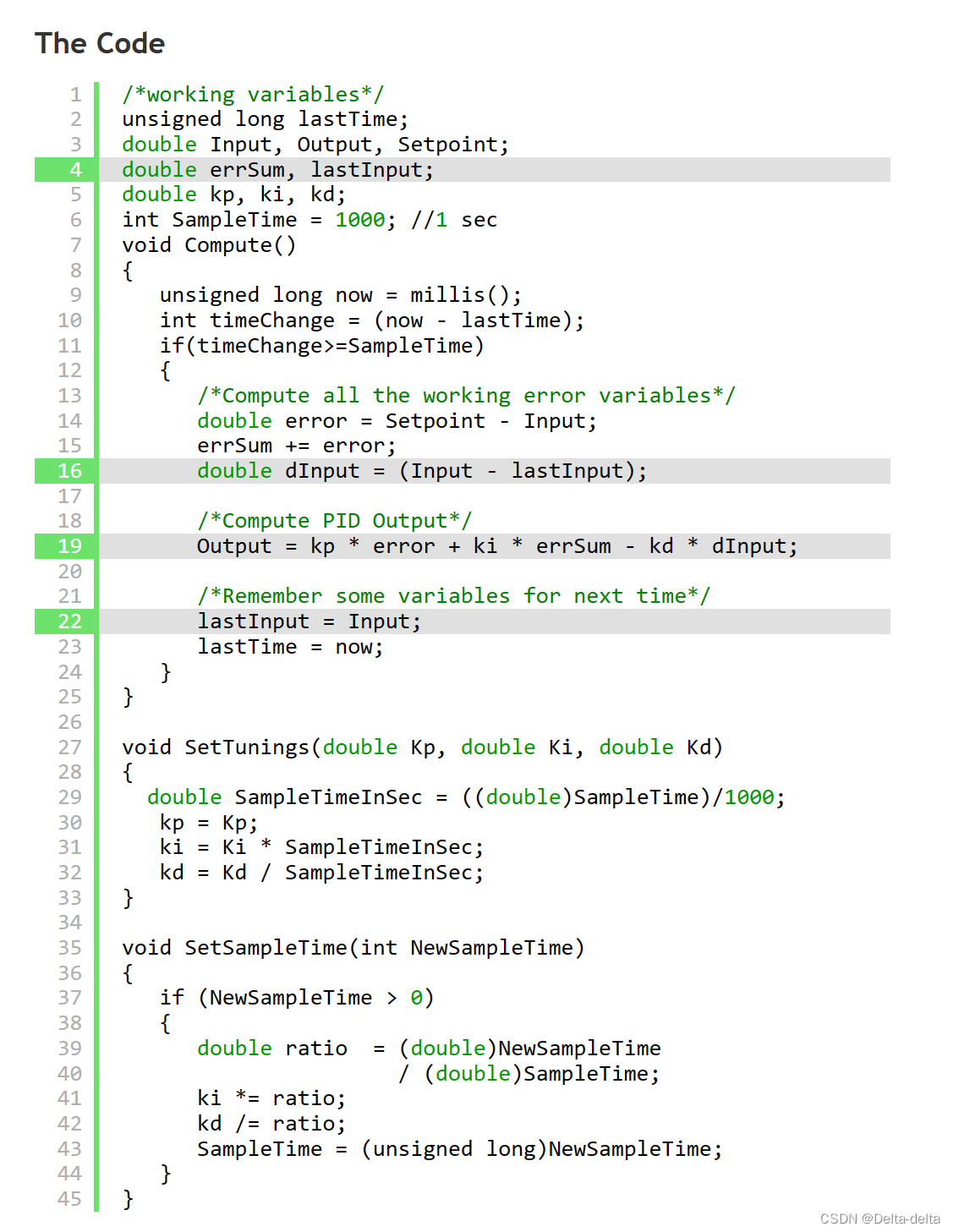
这里的修改非常容易。我们将+dError替换为-dInput。我们现在记住的不是lastError,而是lastInput.
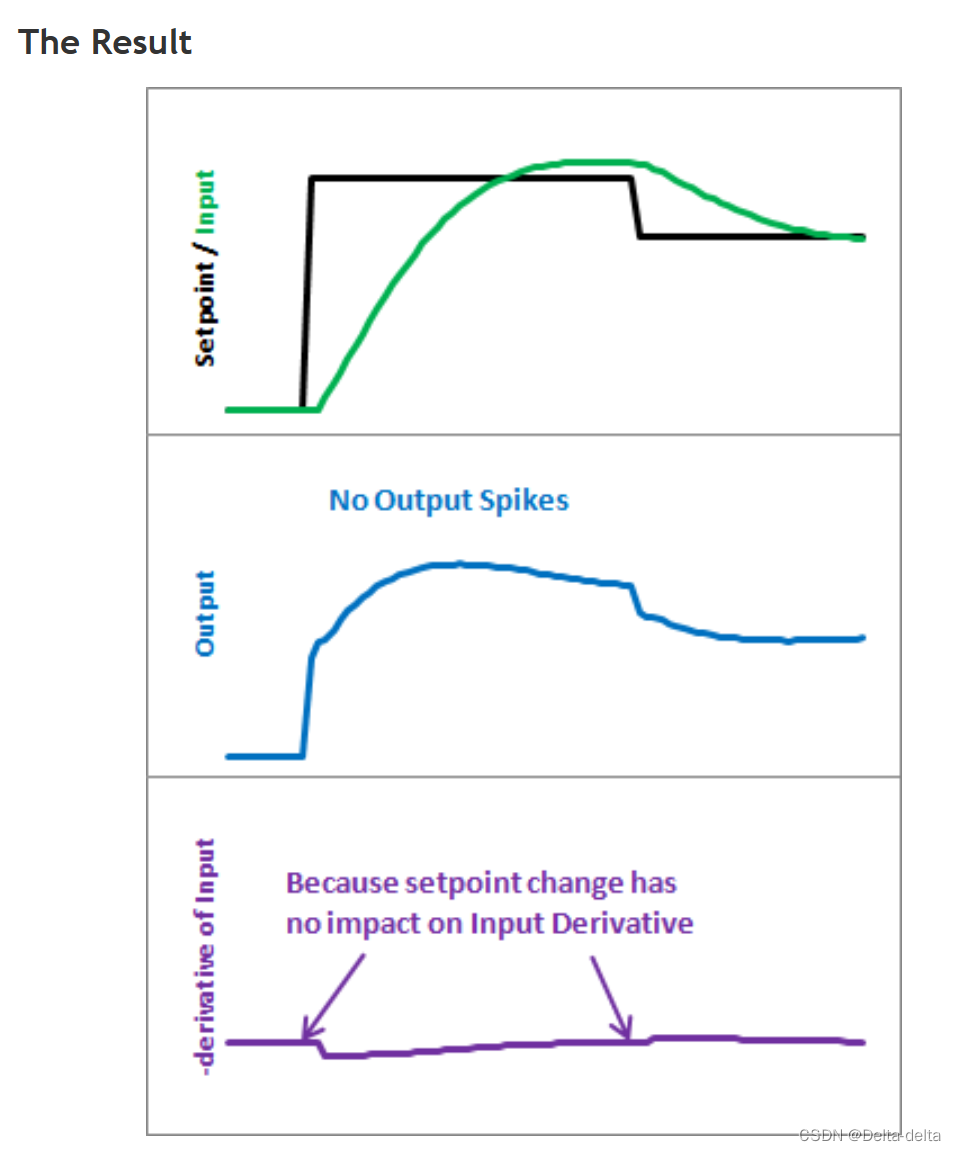
以下是这些修改给我们带来的结果。请注意,输入看起来仍然大致相同。因此,我们获得了相同的性能,但并不是每次设定值发生变化时都会发出巨大的输出峰值。



![[SwiftUI]自定义滚动菜单栏进行PageView页面切换](https://img-blog.csdnimg.cn/direct/3caf93b5b51c45b99241c81894c8aee6.gif)