检测 是发现问题
诊断 是找到原因

误差的分类

1. 系统误差：系统误差是由于仪器本身不精确，或实验方法粗略，或实验原理不完善而产生的。
2. 随机误差：随机误差是由各种偶然因素对实验者、测量仪器、被测物理量的影响而产生的。
3. 粗大误差：粗大误差是明显超出测定条件下预期的误差，即是明显歪曲检测结果的误差，应想办法予以发现和剔除。

环比和同比

• 同比
  同比是指与去年同期相比的数据变化率。它通常用于衡量某一时期与去年同期相比的增长或下降情况。通过同比分析，我们可以快速了解当前市场状况与去年同期相比的变化趋势。
  计算方法：同比变化率 = (本期数值 - 去年同期数值) / 去年同期数值 × 100%
• 环比
  环比是指与上一统计周期相比的数据变化率。它通常用于反映近期数据的变化趋势。通过环比分析，我们可以更好地了解数据随时间推移的发展趋势。
  计算方法：环比变化率 = (本期数值 - 上期数值) / 上期数值 × 100%

均值、方差、标准差

小概率事件： 在统计学中把概率小于0.05或0.01的事件称为小概率事件。
显著性水平： 在统计假设检验中，公认的小概率事件的概率值被称为统计假设检验的显著性水平。
置信度： 置信区间包含总体参数的确信程度，即1-α。
例如：95%的置信度表明有95%的确信度相信置信区间包含总体参数（假设进行100次抽样，有95次计算出的置信区间包含总体参数）。

临界值： 与检验统计量的具体值进行比较的值。是在概率密度分布图上的分位数。这个分位数在实际计算中比较麻烦，它需要对数据分布的密度函数积分来获得。

假设检验原理
在假设检验过程中,通常会将观察到的统计量与一个临界值进行比较,若观察到的统计量大于或小于临界值，则认为该统计量有显著性差异或无显著性差异。

假设检验：以样本服从二项分布举例

1. 背景

指标与业务息息相关，其价值在于发现问题和发现亮点,以便及时地解决问题和推广亮点。随着电商业务的进一步发展，业务迭代快、逻辑复杂，指标的数量越来越多，而且指标之间的差异非常大，变化非常快，如何能够快速识别系统各项异常指标，发现问题的根因，对业务来说至关重要。 如果通过手动的方式去设置报警阈值容易出现疏漏，且非常耗时，成本较高。我们希望构建一套自动化方法，能够达成以下目标：

• 自动化： 无需依赖用户输入。传统的方式是需要定义异常规则、归因维度等等，在自动化系统中不再需要用户手动输入。
• 通用性：能够适应多种多样的指标分布，不同的指标匹配不同的方法。
• 时效性：实现天级、小时级的指标异常检测和归因。
  准确性和主动性：实现数据找人的目标。

接下来将分别介绍指标异常检测、指标异常诊断。

2. 指标异常检测

1.异常的分类

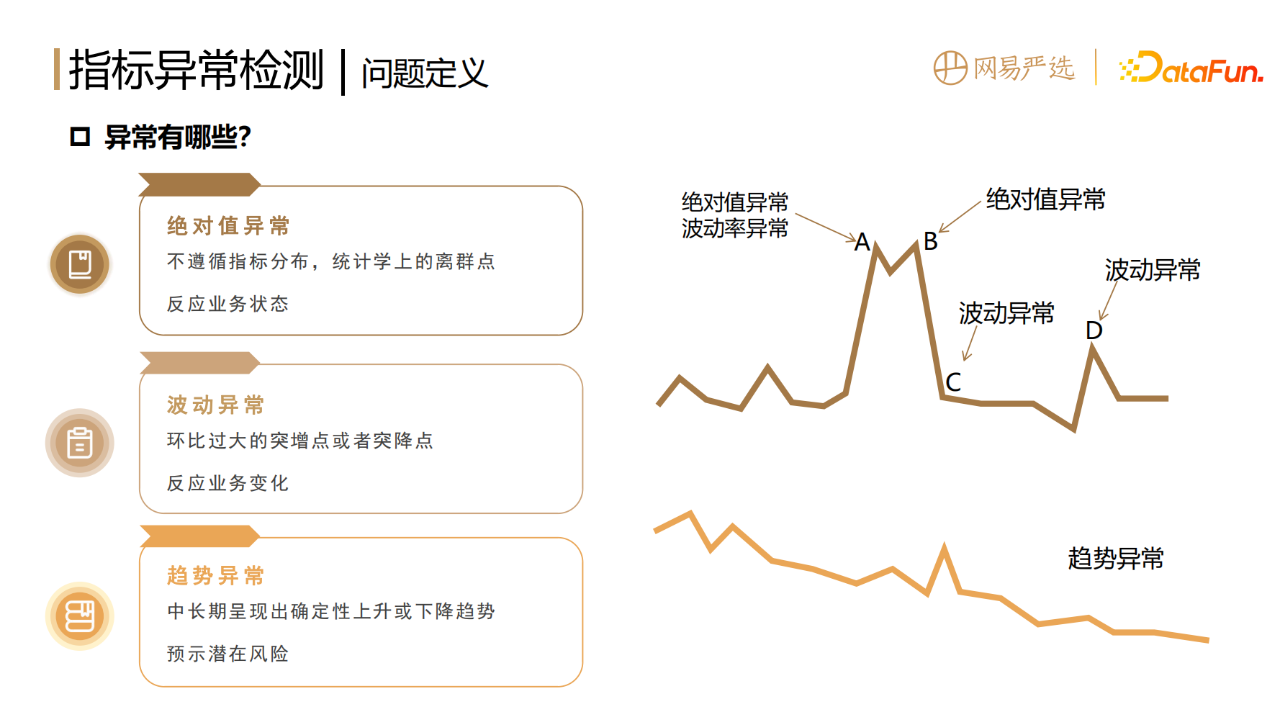
数据指标的异常，指标的过高过低、大起大落都不正常，都需要进行预警和诊断。指标的异常分为以下三种：

1. 绝对值异常（单点异常）
指的是不遵循指标固有的分布，在统计学上的离群点，它反映的是业务当下的状态。
2. 波动异常
环比过大的突增点或者突降点，反映的是业务当下突然的变化。
3. 趋势异常
前两种异常是偏单点的，是短暂剧烈的，而有些异常则相对隐蔽，是在中长期呈现出确定性上升或者下降的趋势，往往预示着某些潜在的风险，所以我们也要进行趋势的异常检测，进行业务预警和提前干预。

指标异常检测算法

1.绝对值异常检测

1. 3Sigma准则
   适用分布：正态分布
   
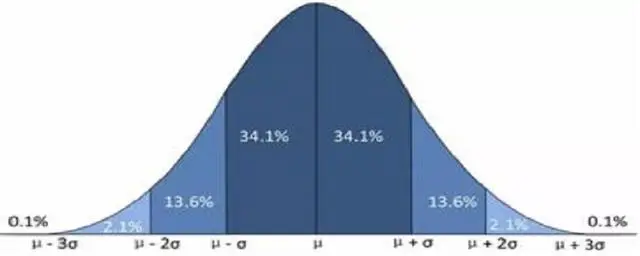
   3σ(西格玛)准则又称为拉依达准则，它是先假设一组检测数据只含有随机误差，对其进行计算处理得到标准偏差，按一定概率确定一个区间，认为凡超过这个区间的误差，就不属于随机误差而是粗大误差，含有该误差的数据应予以剔除。

3σ准则可以用于剔除粗大误差。
缺点：检出率过低（小于1%），只能检出非常极端异常的问题。

2. IQR(Interquartile Range)方法
   

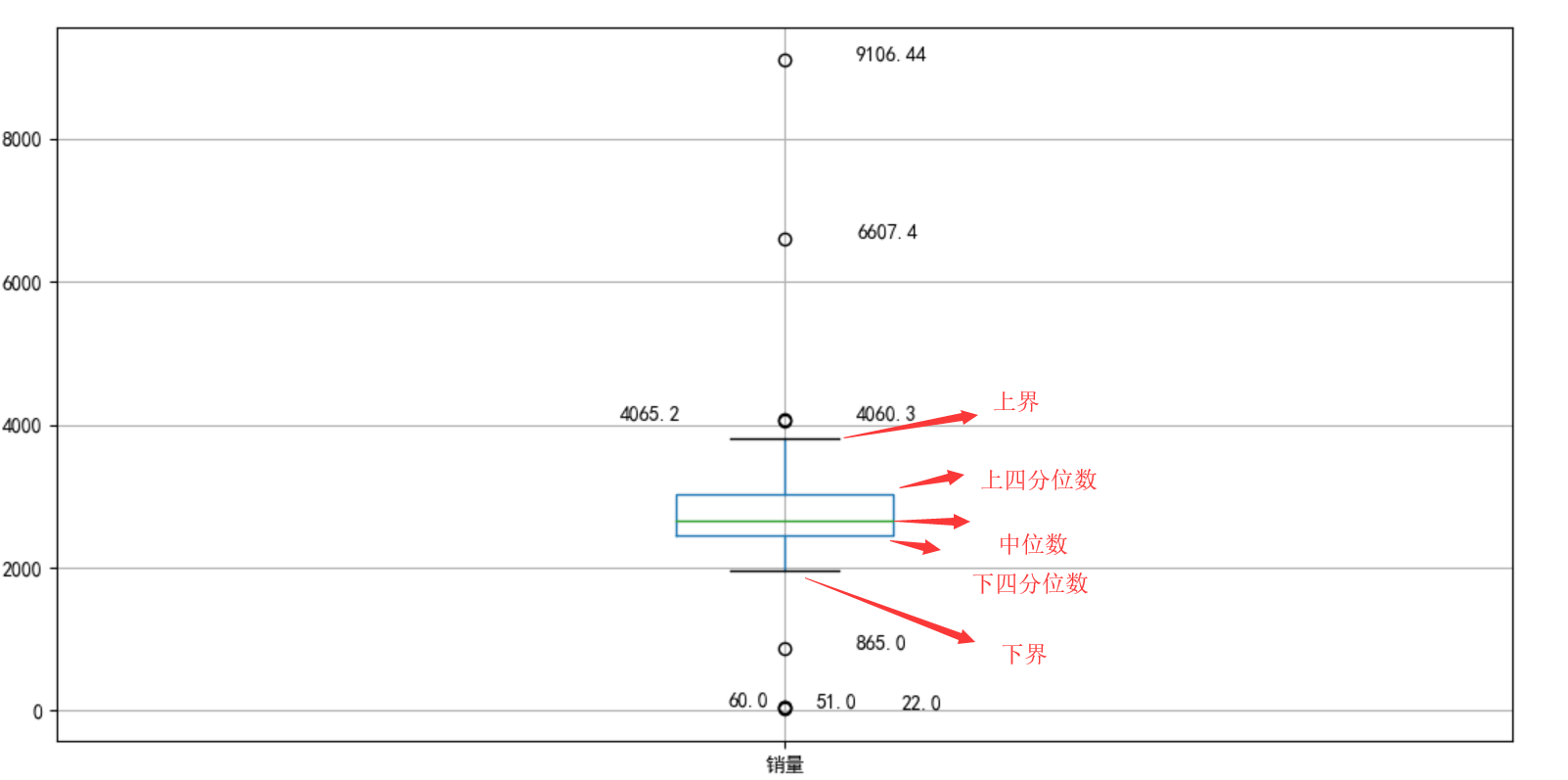
适用分布：非正态分布
根据数据的四分位数范围来判断数据是否为异常值。 IQR通过将数据集分成四个相等的四分位数来测量变异性。首先，将整个数据按升序排序，然后将其分成四个相等的四分位数，分别称为 Q1、Q2、Q3 和Q4
计算第一和第三四分位数（Q1、Q3），异常值是位于四分位数范围之外的数据点xi，k一般取1.5或3：

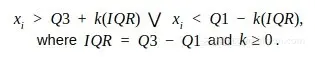
quantile函数

示例：

# quantile函数
def quantile(data, quantile):
    sorted_data = sorted(data)
    position = (len(data) - 1) * quantile
    result = sorted_data[int(position)]
    return result

# 计算异常值
def outlier(series):
    # 计算第一四分位数
    Q1 = quantile(data, 0.25)
    print("第一四分位数:", Q1)
    # 计算中位数
    Q2 = quantile(data, 0.5)
    print("中位数:", Q2)
    # 计算第三四分位数
    Q3 = quantile(data, 0.75)
    print("第三四分位数:", Q3)
    #四分位间距IQR
    IQR=Q3-Q1
    print("四分位间距：",IQR)
    #下限
    low=Q1-1.5*IQR
    print("下限：",low)
    #上限
    upper=Q3+1.5*IQR
    print("上限：",upper)

    result =[]
    for num in series:
        if num < low:
            result.append(num)
        if num > upper :
            result.append(num)
    return result

if __name__ == "__main__":
    data = [30,31,32,32,32,35,35,35,35,35,37,49,56,56,56,57,57,57,58,59,60,60,60,80,92,100]
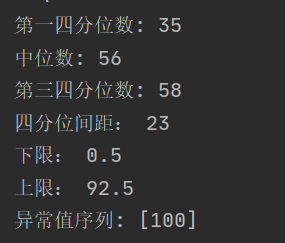
    print("异常值序列:",outlier(data))

结果：

3. GESD检验算法
   适用分布：正态分布
   首先绝对值检测主要是基于GESD检验算法，它的原理是通过计算统计量来寻找异常点。过程如下：

   1. 假设数据集中有最多r个异常值。 第一步先找到离均值最大的样本i，然后计算 统计量Ri ，即xi减去均值后的绝对值，除以标准差。
      

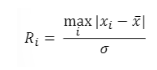
   2. 接下来计算对应的样本点i的临界值λi，其中的参数n 是总共的样本量，i是已剔除的第几个样本，tp,n-i-1是具有 n-i-1自由度的t 分布的p 百分点，而p与设定的置信度α（一般α取值为0.05）及当前样本量有关。
      

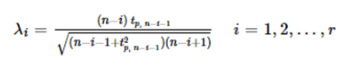
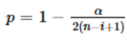
   3. 第三步是通过剔除离均值最大的样本i，然后重复上面步骤，一共r次。

   4. 第四步寻找统计量 Ri 大于λi的样本，即为异常点。

H0:｜u｜<=u0
H1:｜u｜>u0
GESD用的是双边检验，详情参考Grubbs TEST

这种方法的优点：
一是无需指定异常值的个数，只需要设定异常的上限，在上限范围内，算法会自动捕捉异常点；
二是克服了3Sigma检出率过低（小于1%），只能检出非常极端异常的问题。

在GESD算法中可以通过控制检出率的上限去做适应，但是这个方法的前提是要求输入的指标是正态分布。我们目前观测的电商业务指标绝大多数是属于正态分布的，当然也有个别业务指标（<5%）属于非正态分布，需要采用其他方法来兜底，如quantile。

2.波动异常检测

适用分布：正态分布or非正态分布
主要是基于波动率分布，计算分布的拐点。
这里不能直接对波动率分布套用上面的办法，主要是因为指标波动率绝大多数不是正态分布所以不适用。找拐点的原理是基于二阶导数和距离来寻找曲线上的最大弯曲点。

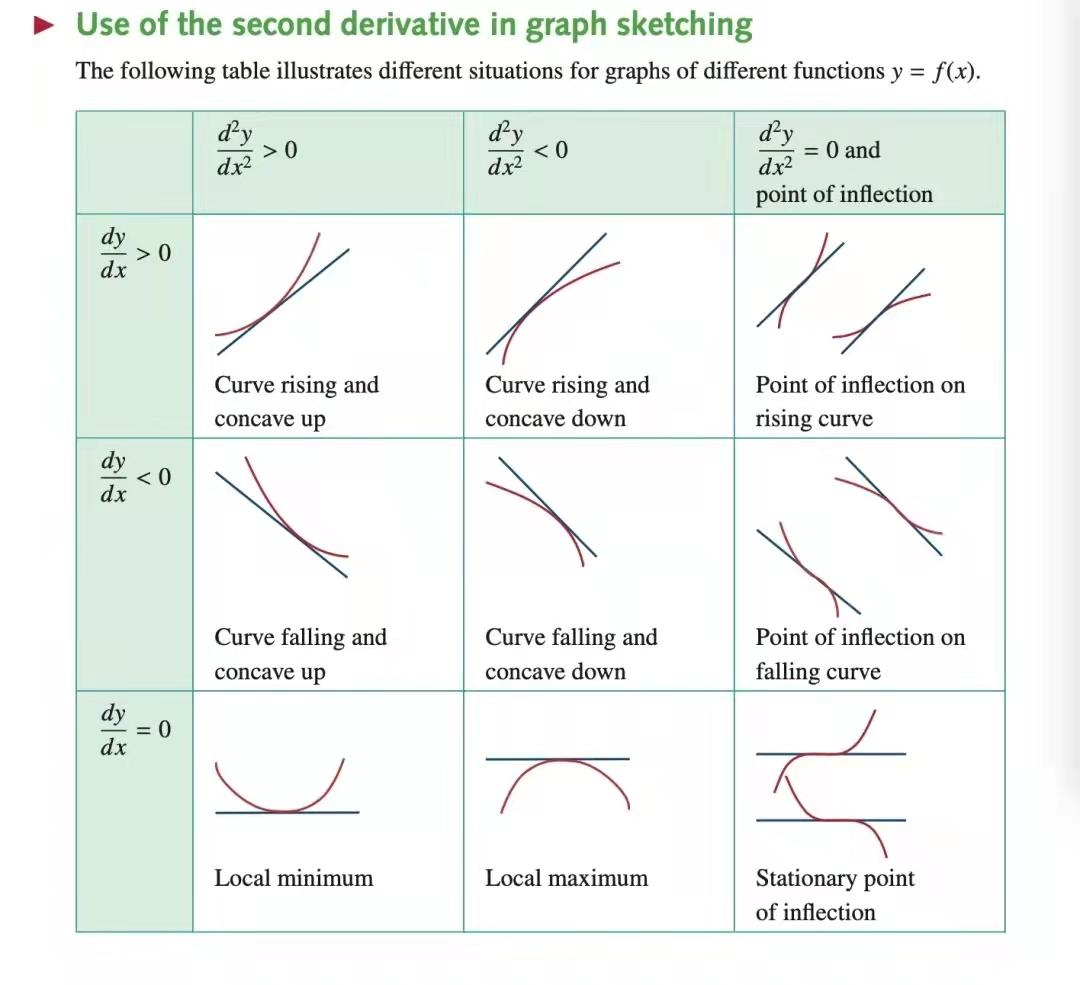
增长的波动率大于 0，下降的波动率小于 0，针对在 y 轴两侧大于 0 和小于 0 的部分，分别要找两个波动率的拐点，波动率超出拐点的范围，就认为是波动异常。但个别情况下拐点会不存在，或者拐点来得太早，导致检出率太高，所以也需要其他的方法来兜底，如quantile。一种检验方法不是万能的，需要组合来使用。

（目前理解是环比大于某个阈值则可能有异常）

3.趋势异常检测

适用于所有的分布
Mann-Kendall检验
第三种是趋势异常检测，基于Mann-Kendall检验。

1. 先计算统计量S， 其中sgn 是符号函数，根据指标序列前后值的相对大小关系，两两配对可以得到 -1、1、0 这样3个映射值。
2. 对统计量S做标准化，就得到了Z，Z服从标准正态分布。可以通过查表的方式换算到p值。统计学上当 p 值小于 0.05，就认为有显著性的趋势。

衡量趋势大小的指标，用倾斜度β表示为：

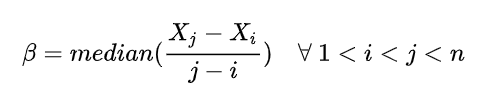
median表示中位数，β为正值表示“上升趋势”，β为负值表示“下降趋势”。

Mann-Kendall用的是双边检验， H0没有单调趋势，相当于整体值趋势~等于0；H1有单调趋势，整体趋势可能为负，可能为正。

优点：
优点一是非参数检验，即可以适用于所有的分布，因此不需要兜底方法。
优点二是不要求指标序列连续，因为在进行趋势异常检测的时候，需要事先剔除绝对值异常的样本，所以大多数指标序列并不连续，但这个方法是可以支持指标不连续的。

4.异常检测后处理

三种异常结束之后，需要进行后处理的工作，其目的主要是减少不必要的报警，降低对业务的打扰。

第一种是数据异常，这的数据异常不是指数据源出错了，因为数据源是在数仓层面，由数仓团队来保证。这里的数据异常指的是上周期的异常导致了本周期的波动异常，比如某个指标昨天上涨了100%，今天又下降了50%，这种情况就需要基于规则来进行剔除，剔除的条件就是：
（1）上个周期存在波动或绝对值异常。
（2）本周期的波动属于回归正常的，即有波动异常但无和波动异常同向的绝对值异常。
比如昨天上涨了100%，今天下降 50% ，经后处理模块会过滤掉，但是如果下降了99%，此时触发了绝对值异常还是需要预警的。通过这种方式我们一共剔除了40% 以上的波动异常。
第二种 后处理是基于S级大促的信息协同，这种大促中每个小时都可能会出现指标的异常，大家都知道原因，因此没有必要去进行播报。

指标异常诊断

1. 诊断层次和对应方法比较

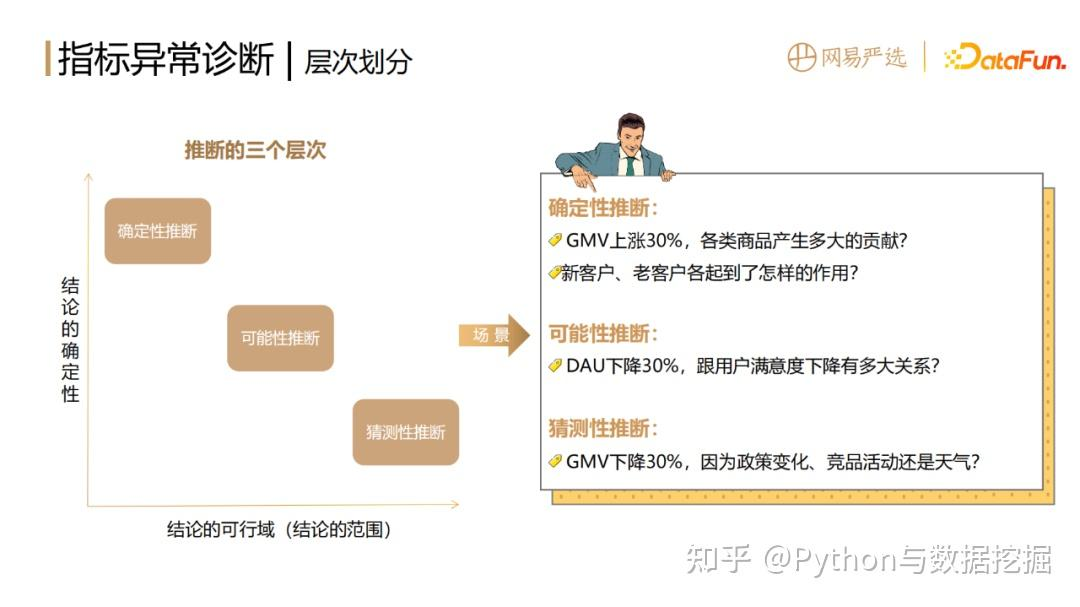
根据结论的可行域和确定性，可以将推断分为三个层次，三个层次对应不同方法：

• 确定性推断
  主要是基于拆解贡献度算法。拆解贡献度算法不管是加法、乘法还是除法，都是按照拆解方式来衡量各部分指标或者结构的变化对整体的影响。
  优点，是确定性比较强，白盒化，适应性比较强，能够精准定位到异常所在的位置。
  缺点，就是针对同一个指标，有非常多的维度可以去拆解，会带来组合维度爆炸的问题。
• 可能性推断
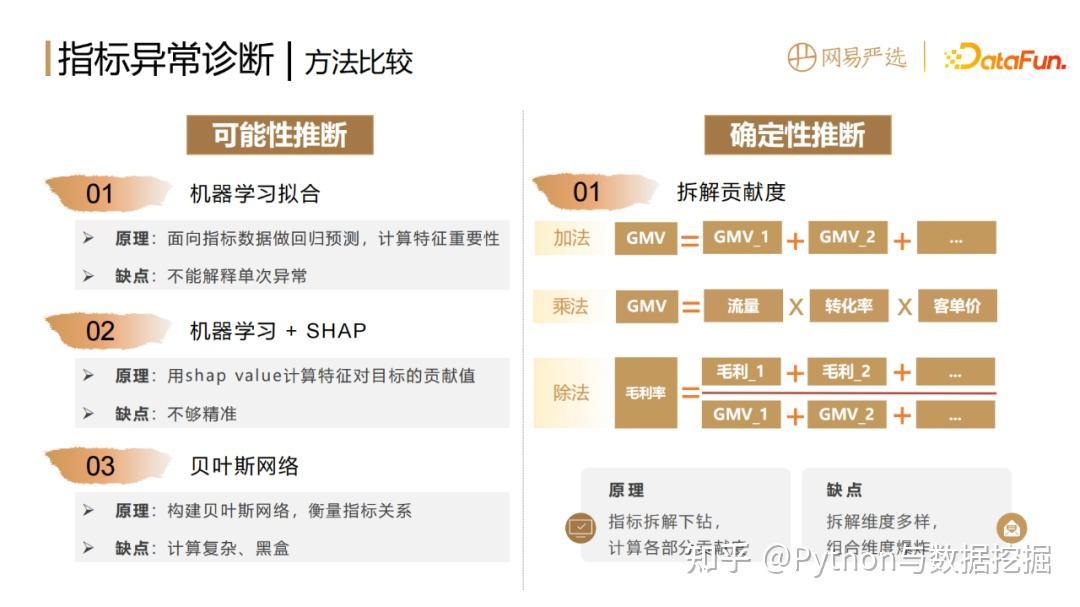
  （1）可以基于机器学习去拟合指标数据，做回归预测，计算特征的重要性，这种方法的缺点是不能解释单次异常的原因。
  （2）如果想解释单次的异常要加上一个 shap value 算法，它可以计算每一次预测值，每一个输入特征对于目标的贡献值。这种方法具有一定的可解释性，但是不够精准，而且只能得出相关性，并非因果性。
  （3）可以通过贝叶斯网络来构建指标间关系的图和网络，但缺点是计算相对复杂，并且黑盒。
• 猜测性推断
  结论主要依赖人的经验，结论相对不明确，可操作空间有限，不在本文的方法讨论范围之内。

2. 指标分级——以品牌电商为例

品牌电商的指标分级可以分为

• 战略层
  一级指标，即北极星指标。比如大盘的GMV，它衡量的是目标的达成情况，服务于公司的战略决策。
• 战术层
  二级指标，是通过将一级指标分拆到各级部门和业务线得到的，服务的是过程管理。
• 执行层
  三级指标，是将二级指标进一步拆分到各级类目商品以及负责人，服务具体实施。

3. 指标拆分和贡献度

指标拆分

指标拆分应该满足MECE分析法，即不遗漏，不重叠将某个整体拆分成不同部分，且保证拆分后的各部分符合以下要求：
1.各部分之间相互独立（Mutually Exclusive）
2.所有部分完全穷尽（Collectively Exhaustive）

常用指标维度拆分方向，如下图：

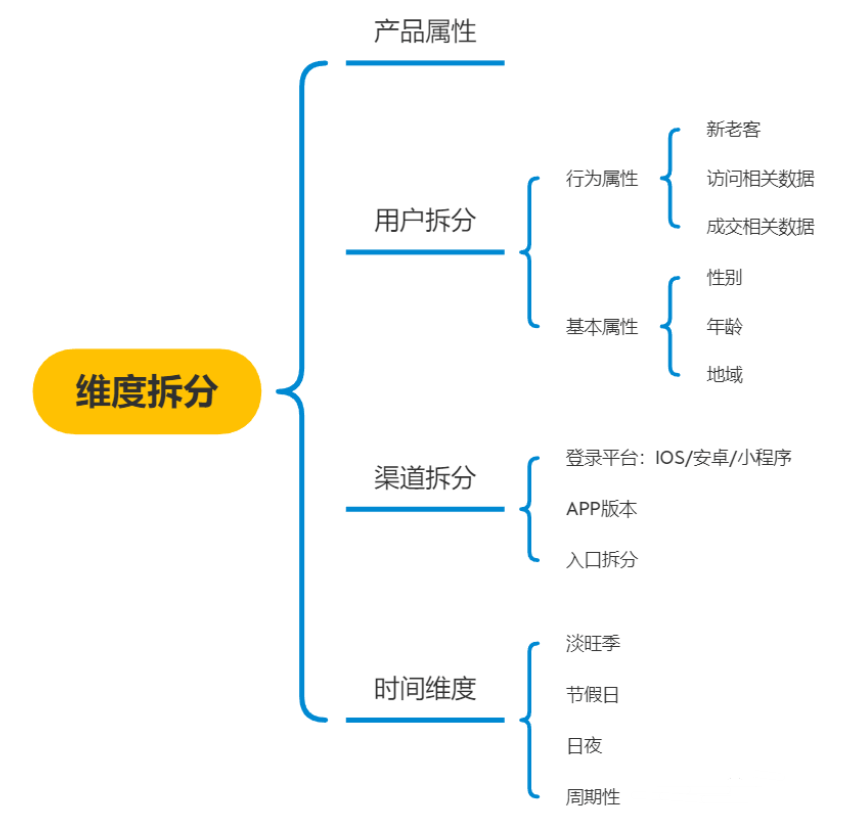
指标的分类

加法型指标：具有可加性的量值指标，例如大盘DAU = 各个渠道的DAU之和
乘法型指标：常为涉及到流程链路的指标，例如某页面访问UV = DAU * 该页面访问转化率
除法型指标：从量值指标衍生而出的率值指标，例如pv点击率 = 点击pv / 浏览pv

什么是贡献度

贡献度，即用定量衡量的方式来说明：
一个指标$Y$的异动 $△Y$ ，具体是由其中哪些成分$X_i$带来了多少异动$△Y_i$？

4. 拆解贡献度计算方法

拆解方法如上图中所示。Y是要进行拆解的目标指标，比如大盘的GMV（网站的成交金额），$X_i$是其下某个拆分维度下第 i 个维值，比如某个省市的GMV，$X_i^1$代表当前周期的指标，$X_i^0$表示上一个周期的原始值。

变化比 $△Y$%=$=\frac{Y_1-Y_0}{Y_0}$

贡献度的计算方式包括三种：

加法
加法的拆解公式很好理解，每个维值的变化值$\Delta X_i$除以整体的原始值$Y_0$，就是它的贡献度$D{X}_i$。各构成要素的贡献$D{X}_i$加起来等于$△Y$% 。

▌实例

例如针对大盘DAU本月环比上月-6.29%
大盘DAU = 各个渠道的DAU之和
欲从渠道角度拆解，定量衡量各渠道对于异动变化的贡献：

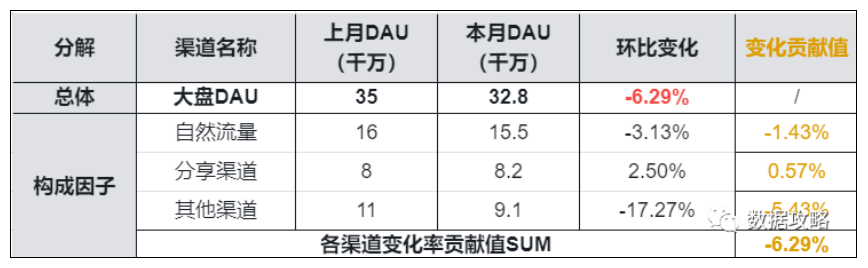
乘法
乘法拆解采用了LMDI（Logarithmic Mean Index Method）乘积因子拆解的方式。两边同时取对数ln，即可得到加法形式，再按照上述方法，就可以得到各因子的贡献度。维值的前后比率比较大，贡献度就比较大。

▌实例

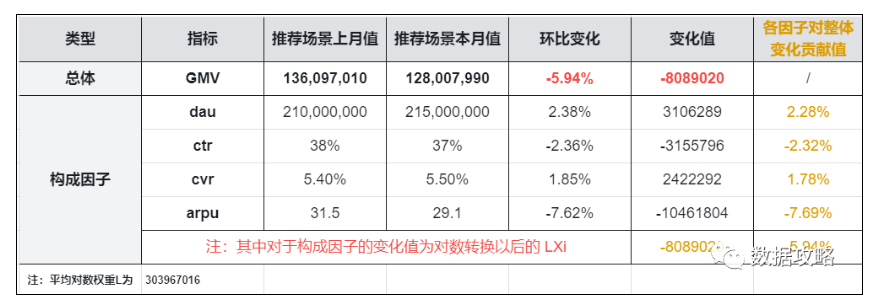
例如以淘宝搜索场景的产出为例
产出构成可以拆解为：
访问场景的流量、用户购买转化率、客单价。
分别与大盘用户增长规模、场景转化能力、用户购买偏好等指标有关。
此类拆解方式，将场景的产出总体以流量、效率两大方面进行分析即：

商品交易总额GMV=日活跃用户数量DAU * 点击且转化的概率CR(即CTR点击率 * CVR转化率)* 客单价ARPU

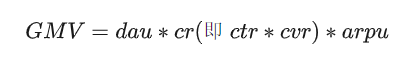
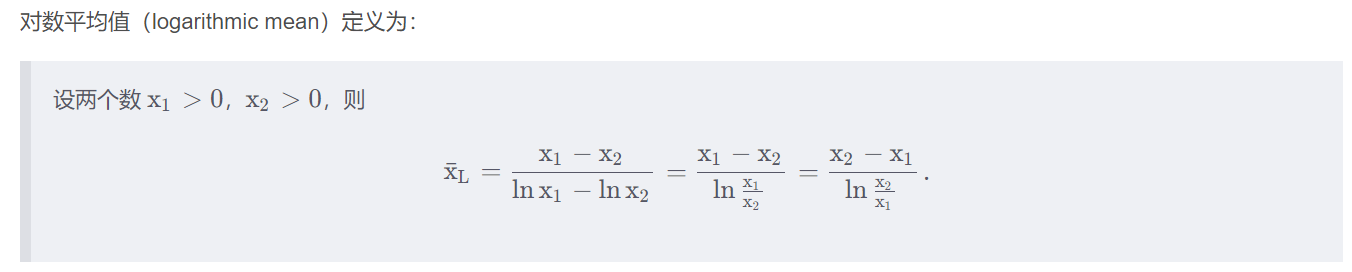
假设搜索常见GMV本月环比上月-5.94%。
欲从购买漏斗流程拆解，定量衡量各环节对于变化的贡献：
第一步：计算将乘法形式转化为对数形式所需的平均对数权重$L(Y_1-Y_0)$

$L(Y_1-Y_0)=\frac{Y_1-Y_0}{ln{Y}_1-ln{Y}_0}$

第二步：计算各因子指标的对数形式变化值$L{X}_i$，如表格倒数第二列。

$L(X_i)=\frac{Y_1-Y_0}{ln{Y}_1-ln{Y}_0}\ast ln\frac{X_{i_1}}{X_{i_0}}=L(Y_1-Y_0)\ast (ln{X}_{i_1}-ln{X}_{i_0})$

第三步：计算各因子指标对于总GMV环比变化的贡献$D{X}_i=L{X}_i/Y_0$，如表格最后一列。

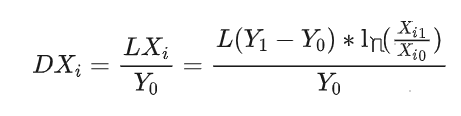
除法
除法采用双因素拆解方法，即每一个部分、每一个维值对整体的贡献度是由两个因素构成。
第一个因素是波动贡献，用$A_{X_i}$表示；
第二个因素是结构变化贡献$B_{X_i}$，即每部分的结构变化贡献。举个例子，每个部门的毛利率都提升了但整个公司的毛利率却下降了。原因大概率就是某个低毛利的部门销售占比变大了，拖垮了整体，也就是我们熟知的辛普森悖论的情况。除法拆解算法中，引入$B_{X_i}$这部分结构变化的贡献，就能够解决这个问题。

贡献度的一个很重要的特性就是可加性，满足 MECE 不重不漏的原则。不管哪种拆解方式，把某个拆解维度下的全部维值贡献$D_{X_i}$进行加和，都可以得到整体的变化率ΔY%。