文章目录
- 前言
- 有向无环图的最小路径点覆盖
- 概念
- 拆点二分图
- 定理
- **证明**
- 最小路径可重复覆盖
- 解决策略
- 代码实现
- OJ练习
前言
关于二分图:二分图及染色法判定
关于二分图最大匹配:二分图最大匹配——匈牙利算法详解
关于二分图带权最大完备匹配:二分图带权最大匹配-KM算法详解
有向无环图的最小路径点覆盖
概念
给定一张有向无环图,要求用尽量少的不相交的简单路径,覆盖有向无环图的所有顶点(也就是每个顶点恰好被覆盖一次)。这个问题被称为有向无环图的最小路径点覆盖,简称**“最小路径覆盖”**。
拆点二分图
设原来的有向无环图为G = (V , E), n = |V|。 把G中的每个点x拆成编号为x和x+n的两个点。建立一张新的二分图,1~n作为二分图左部点,n + 1 ~ 2n作为二分图右部点,对于原图的每条有向边(x,y), 在二分图的左部点x与右部点y+n之间连边。最终得到的二分图称为G的拆点二分图,记为G’。例如:
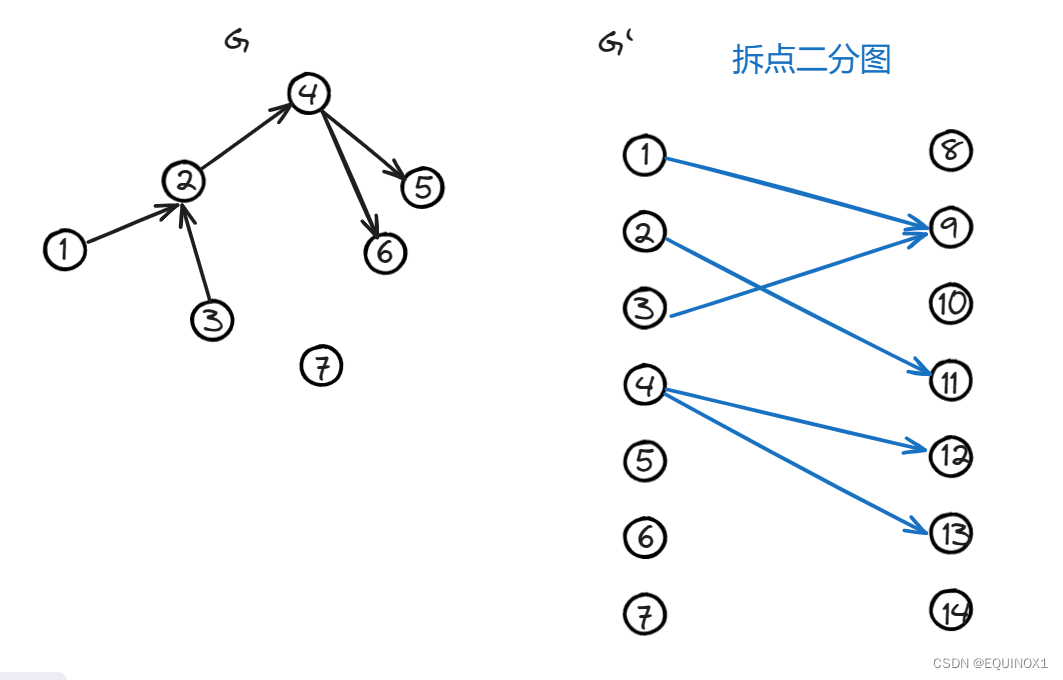
定理
有向无环图G的最小路径点覆盖包含的路径条数,等于n减去拆点二分图G’的最大匹配数。
证明
在有向无环图G= (V,E)的最小路径覆盖中,对于任意的x ∈ V,因为路径不相交,所以x的入度和出度都不超过1。因为每个节点都被覆盖,所以x的入度和出度至少有一个是1。
因此,最小路径覆盖中的所有边,在拆点二分图G‘中构成一组匹配。最小路径覆盖中每条边(x,y) 的起点x与拆点二分图每条匹配边(x,y+n)的左部点x是一一对应的。
特别地,对于每条路径的终点t,因为t没有出边,所以在二分图中,t匹配失败。即路径的终点和拆点二分图左部的非匹配点是一一对应的。
故有:路径覆盖包含的路径条数最少
等价于 路径的终点数(出度为0的点数)最少
等价于 拆点二分图左部非匹配点最少
等价于 拆点二分图匹配数最大
故G的最小路径覆盖的路径数等于n减去拆点二分图G‘的最大匹配数。
证毕。
最小路径可重复覆盖
给定一张有向无环图,要求用尽量少的可相交的简单路径,覆盖有向无环图的所有顶点(也就是一个节点可以被覆盖多次)。这个问题被称为有向无环图的最小路径可重复点覆盖。
解决策略
在最小路径可重复点覆盖中,若两条路径:…→u→p→v→…和…→x→p→y→…在点p相交,则我们在原图中添加一条边(x,y),让第二条路径直接走x→y,就可以避免重复覆盖点p。
进一步地,如果我们把原图中所有间接连通的点对x,y直接连上有向边(x,y),那么任何“有路径相交的点覆盖”一定都能转化成“没有路径相交的点覆盖”。实际上,转化后的拆点二分图的未匹配左部点仍为最小可相交路径数目,例如: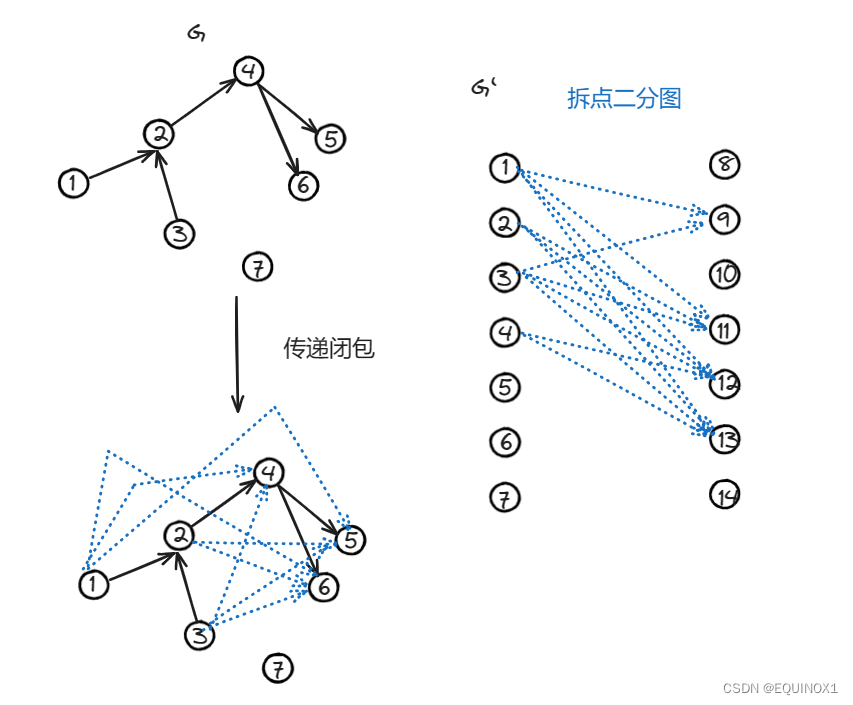
综上所述,有向无环图G的最小路径可重复点覆盖,等价于先对有向图传递闭包,得到有向无环图G’,再在G’上求一般的(路径不可相交的)最小路径点覆盖。
代码实现
#define int long long
#define N 205
int n, m, match[N]{0}, ans = 0;
bool vis[N], g[N][N]{0};//邻接矩阵存图
//匈牙利
bool dfs(int u)
{
for (int v = 1; v <= n; v++)
if (!vis[v] && g[u][v])
{
vis[v] = true;
if (!match[v] || dfs(match[v]))
{
match[v] = u;
return true;
}
}
return false;
}
//main
// Floyd求传递闭包
for (int i = 1; i <= n; i++)
g[i][i] = true;
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
g[i][j] |= g[i][k] && g[k][j];
for (int i = 1; i <= n; i++)
g[i][i] = false;
for (int i = 1; i <= n; i++)
memset(vis, 0, sizeof(vis)), ans += dfs(i);
cout << n - ans;
OJ练习
379. 捉迷藏 - AcWing题库
这道题目的最大藏身点数目就是给定的有向无环图的最小路径可重复覆盖数目。
设最大藏身点集合为hide,最小路径可重复覆盖为path,往证hide = path:
显然藏身点不能在同一条路径上,而path包含了所有的点,所以每条path最多选一个藏身点,故|hide| <= |path|
如果我们能在path上构造出|path|个藏身点,那么就得证了,因为|hide|是最大藏身点数目,而最大又不超过|path|。
求path很容易,我们即然能求出最小覆盖,自然能还原出路径:
- 对于每条path的终点即为拆点二分图非匹配点,这个显然很好求
- 非匹配点x的右部拆点为x + n,那么通过match[x + n]可以找到x在path的邻接点y,同样的方法一直往下进行,可以还原出path
问题在于如何从每条path上选出一个藏身点:
- 记path终点集合为E,从E发出的边往下走,访问到的节点集合为next(E)
- 若E ∩ next(E) = Ø,即藏身点之间无路径,那么E 可以作为 hide
- 否则,对于E ∩ next(E)中的 每个节点e,沿着路径往回走,总能找到e’ ∉ next(E),否则path数目会减少,和最小覆盖矛盾
- 找到e’后删除e,再重复3,直到E ∩ next(E) = Ø,此时E即为符合条件的hide
证毕
AC代码如下:
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
#include <climits>
#include <cmath>
#include <functional>
using namespace std;
#define int long long
#define N 205
int n, m, match[N]{0}, ans = 0;
bool vis[N], g[N][N]{0};
bool dfs(int u)
{
for (int v = 1; v <= n; v++)
if (!vis[v] && g[u][v])
{
vis[v] = true;
if (!match[v] || dfs(match[v]))
{
match[v] = u;
return true;
}
}
return false;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
//freopen("in.txt", "r", stdin);
cin >> n >> m;
for (int i = 0, a, b; i < m; i++)
{
cin >> a >> b;
g[a][b] = true;
}
for (int i = 1; i <= n; i++)
g[i][i] = true;
// 传递闭包
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
g[i][j] |= g[i][k] && g[k][j];
for (int i = 1; i <= n; i++)
g[i][i] = false;
for (int i = 1; i <= n; i++)
memset(vis, 0, sizeof(vis)), ans += dfs(i);
cout << n - ans;
return 0;
}