今天AC了三个题目：

第一个题目：P4913 【深基16.例3】二叉树深度

(1条消息) P4913 【深基16.例3】二叉树深度_lxh0113的博客-CSDN博客

第二个题目：P1229 遍历问题

(1条消息) P1229 遍历问题_lxh0113的博客-CSDN博客

第三个题目：P2835 刻录光盘

(1条消息) P2835 刻录光盘_lxh0113的博客-CSDN博客

学习了一个新的算法——Kruskal.

Kruskal算法

Kruskal算法是用来产生最小生成树的。什么是最小生成树？

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

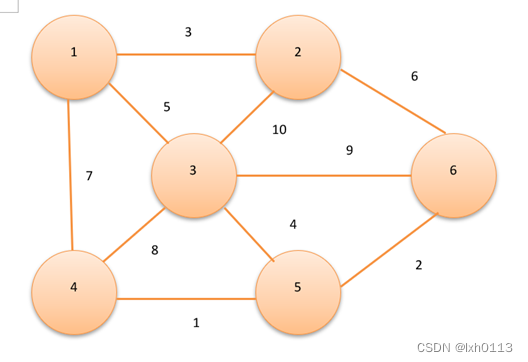
该图的最小生成树是：

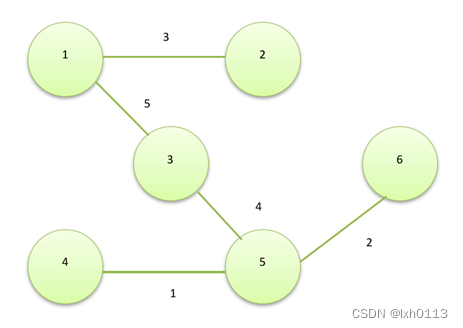
图中绿色的连点是最小生成树。他是最小的能够使连接各个顶点的权重最小。

Kruskal算法就是实现该种算法的。Kruskal算法比较好理解，首先我们需要按照权值排序，排升序。排序的话最好选择快排（如果边不多的话，你也可以选择其他的排序算法）。（后面揭秘）

之所以要排序，是因为我们需要每次选择最小权值的边，判断该条边的起始节点u[i]和v[i]是否连通过，如何判断呢？这是一个重点。前面我们已经学习过了并查集，是的，我们需要使用到它，我们只需要看看他们各自的“爹”是谁即可。如果是一个爹，说明在一个集合中，那么我们就不需要该条边（因为这样子就不满足最小生成树了，他们在一个集合就说明已经连接过了）。

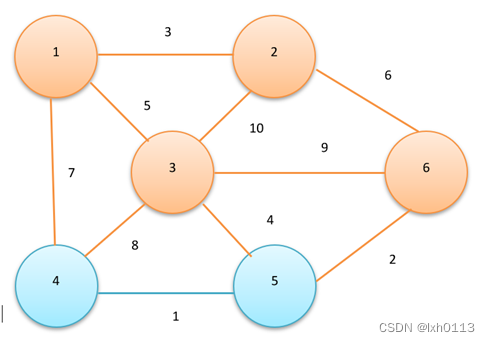
1.先是4-5这条边，符合题意，加进去。

2.然后是5-6这条边，也是符合题意得加进去。

3.然后是1-2，这是符合题意的，加进去。

4.再就是3-5符合题意。

5.然后是1-3也是符合题意，这个时候我们发现已经收集到所有的点了，那么就可以结束循环。

每次选择最小的边，判断是否在一个集合。如果不在一个集合，那么就连接到它。最后我们会得到一个最小生成树。

这就是kruskal的核心算法了。

暂时还没写出kruskal算法的代码。