1.什么是立体视觉几何
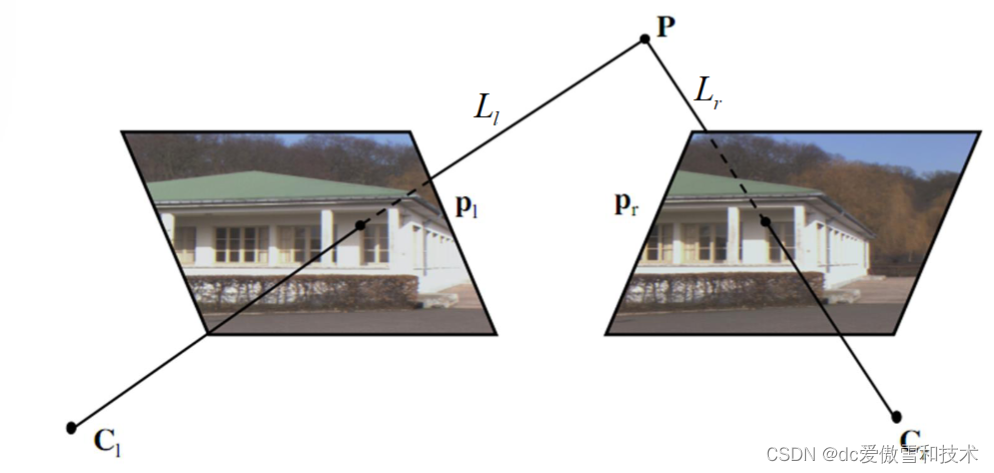
立体视觉=对应+重建:
• 对应:给定一幅图像中的点pl,找到另一幅图像中的对应点pr。
• 重建:给定对应关系(pl, pr),计算空间中相应点的3D 坐标P。
立体视觉:从图像中的投影恢复场景中点的三维位置的过程
类型:基于窗口/局部的算法和全局算法
三角测量:给定pl,我们知道点P位于连接pl和左光心Cl的直线Ll上。**假设我们确切地知道相机的参数,我们可以显式计算 Ll 和 Lr 的参数。**因此,我们可以计算两条直线的交点,即点 P
本地立体算法步骤
◇ 匹配代价计算:SSD、SAD、MSE、MAD
◇ 代价聚合
◇ 视差计算和优化
◇ 视差细化
指用于从一对立体图像(或称为双目图像)中计算深度信息的一系列步骤。在计算机视觉领域,这些算法通过比较同一场景的两个稍有不同视角的图像来估计物体的距离。
-
匹配成本计算:这是立体匹配的第一步。目标是确定立体图像对中的两个像素有多匹配。常见的匹配成本计算方法包括:
- SSD(平方差之和):测量对应图像区块中像素强度的平方差。
- SAD(绝对差之和):类似于SSD,但使用绝对差值。
- MSE(均方误差):区域内平方差的平均值。
- MAD(平均绝对差):区域内绝对差的平均值。
这些方法用于计算每个像素可能视差的成本。成本越低,表示匹配越好。
-
成本聚合:在计算了初步匹配成本之后,通常会在邻域内聚合这些成本,以提高对噪声和无纹理区域的鲁棒性。聚合步骤有助于引入上下文信息,减少初步匹配中不正确匹配的影响。
-
视差计算和优化:这一步涉及为每个像素选择最小化聚合成本的视差值(即在两幅图像中匹配像素之间的水平位移)。可以应用优化方法,如动态规划、图割或半全局匹配,以找到整个图像中最一致的视差值。
-
视差细化:从前一步获得的初步视差图可能存在不准确之处,特别是在物体边界或遮挡区域附近。因此,会采用中值滤波、左右一致性检查(用于识别和纠正遮挡或匹配错误)和亚像素增强等细化步骤,来提高视差图的质量。
通过遵循这些步骤,本地立体声算法可以生成代表场景深度信息的视差图。这个图在3D重建、自主导航和虚拟现实等多种应用中非常关键。
寻找对应
稀疏和密集对应

解决对应问题(correspondence problem)是立体视觉中的一个核心问题,特别是在处理双目(或多目)立体图像时。在这个上下文中,对应问题指的是确定一幅图像中的像素点在另一幅图像中的匹配点。理解这一问题的关键在于了解“极线约束”(epipolar constraints)。
-
二维搜索域的问题: 如果没有任何约束,为了在一幅图像中找到另一幅图像的每个像素点的对应点,理论上需要在整个图像平面上进行搜索。这称为二维搜索域,它导致计算量非常大,且容易产生错误匹配。
-
极线约束(Epipolar Constraints): 幸运的是,在立体视觉中,我们可以利用极线约束来显著减少搜索的复杂度,缩小特征点匹配时的搜索范围。极线约束基于这样一个事实:对于第一幅图像中的任何一个点,其在第二幅图像中的对应点必定位于一条特定的线上,这条线称为极线。
- 极线是由摄像机的几何配置决定的。具体来说,给定第一个摄像机拍摄的一个点,第二个摄像机拍摄的对应点必须位于连接这个点和两个摄像机中心的线与第二个摄像机成像平面的交线上。
- 这意味着,对于第一幅图像中的任何点,我们不需要在第二幅图像的整个平面上搜索其对应点,而只需要在一条线上进行搜索。
-
如何应用极线约束:
- 在实际应用中,首先要确定两个摄像机之间的几何关系,包括它们的位置和方向。这通常通过称为**的过程完成。
- 一旦摄像机被标定,就可以计算出极线,并将搜索对应点的问题从一个二维问题简化为一个一维问题。
- 这样,匹配过程变得更加高效,并且匹配错误的可能性也大大减少。
总之,极线约束是解决立体视觉中对应问题的关键,它通过将复杂的二维搜索问题简化为一维搜索,使得深度估计变得更加可行和精确。
图像校正
图像校正(Rectification)是立体视觉系统中的一项重要技术,它在搜索图像对应点之前通常会被执行,以简化搜索过程。让我们分析一下校正的动机、实现方法和一种简单的解决方案:
动机
- 简化对应点搜索: 在没有校正的情况下,对应点可能位于图像的任何位置,这导致在二维空间中进行搜索。图像校正的主要目的是将这种二维搜索简化为一维搜索,使问题更易于处理。
- 将极线对齐到水平扫描线: 校正后的图像具有这样一个属性,即任一点在另一图像中的对应点位于同一水平扫描线上。这大大降低了匹配算法的复杂度。
实现
- 输入图像校正: 校正过程涉及对输入图像进行变换,以使得对应的水平扫描线成为极线。这意味着,如果在一个图像中找到了一个特征点,那么在另一个图像中的对应点将位于相同的水平位置。
- 独立匹配水平扫描线: 校正后,每一对水平扫描线可以独立匹配,计算匹配分数。这极大简化了算法的复杂度,因为算法只需要在一维空间内(即同一扫描线内)搜索对应点。
简单解决方案:旋转摄像机
- 摄像机旋转: 一种实现图像校正的简单方法是物理地或通过软件旋转两台摄像机,使它们垂直于连接摄像机中心的线(c0 和 c1)。这样做的结果是,摄像机拍摄的图像中的极线会自然地与水平扫描线对齐。
- 对齐效果: 通过这种方式,极线被对齐到水平方向,从而使得在双目立体视觉系统中匹配对应点变得更加简单和直接。
总结
图像校正在立体视觉中扮演着关键角色,它通过简化对应点的搜索过程来提高了系统的效率和匹配的准确性。通过物理或软件方法校正摄像机,可以使得极线对齐到水平扫描线,从而将原本的二维搜索问题转化为一维搜索问题。这不仅简化了计算过程,还提高了匹配的精度和系统的整体性能。
-
同态变换(Homography)的概念:
- 在计算机视觉中,同态变换是一种变换,它可以将一个平面内的点映射到另一个平面内的点。
- 在双目立体视觉系统中,这种变换可以用来调整两个摄像头拍摄的图像,使得它们在一个共同的平面(P)上对齐。
-
映射到共同平面 P:
- 假设有一个平面 P 在空间中,以及两个同态变换 Hl 和 Hr 分别对应于左图像和右图像。
- 这两个变换的作用是将两个图像映射到平面 P 上,同时保证平面 P 平行于连接两个摄像头中心点(Cl 和 Cr)的线。
- 通过这样的映射,两个图像在新的平面 P 上具有相同的视角和几何关系。
-
极线的平行性:
- 当两个图像映射到这样的平面 P 上时,极线(即那些在一个图像中的点可能在另一个图像中找到匹配点的线)会变得平行。
- 这是因为平面 P 被设定为平行于 Cl 和 Cr 连线,所以在校正后的图像中,所有极线都是平行的。
-
极线与图像行的平行性:
- 通过适当选择坐标系,可以确保这些平行的极线与图像的行平行。
- 这意味着,在校正后的图像中,任何一个点的可能匹配点都将位于另一图像的同一行上。
这个过程的关键是通过同态变换将两个图像映射到一个共同的平面上,并调整它们的视角使得极线平行于该平面。通过这种方式,极线也就与图像的行平行,从而将匹配点的搜索简化为在水平行上的一维搜索,大大简化了计算过程,并提高了效率和准确性。这种方法在双目立体视觉系统中广泛应用,特别是在需要高精度和高效率的应用场景中。
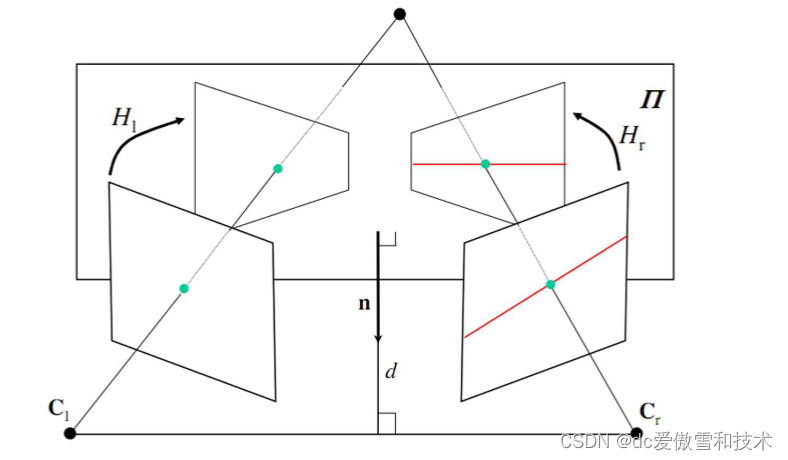
则校正算法为:
• 选择与 CrCl 平行的平面 P
• 定义 P 上的左右图像坐标系
• 根据 P 和虚拟图像的坐标系构造校正矩阵 Hl 和 Hr。