本文借鉴了数学建模清风老师的课件与思路,可以点击查看链接查看清风老师视频讲解:5.1 对数据进行描述性统计以及皮尔逊相关系数的计算方法_哔哩哔哩_bilibili
注:直接先看 ( 三、两个相关系数系数的比较 ) 部分!!!
目录
编辑
一、数据的描述性统计分析
二、皮尔逊相关系数
2.1注意事项
2.2 SPSS绘制散点图
2.3 MATLAB计算皮尔逊相关系数
2.3.1 MATLAB计算皮尔逊相关系数
2.3.2 相关系数矩阵的美化
2.4 对皮尔逊相关系数进行假设检验(p值判断法)
2.4.1 假设检验
2.4.2 MATLAB和SPSS计算p值
①MATLAB计算p值
②spss计算p值
2.5 正态分布检验
2.5.1 JB检验(大样本n > 30)
2.5.2 Shapiro-wilk检验(小样本 3 ≤ n ≤ 50)
2.5.3 QQ图
二、斯皮尔曼相关系数
2.1 斯皮尔曼相关系数
2.2 斯皮尔曼相关系数的计算
2.3 两种相关系数结果的对比
2.4 对斯皮尔曼相关系数进行假设检验(p值判断法)
①matlab计算P值
②SPSS计算p值
三、两个相关系数系数的比较
一、数据的描述性统计分析

clear;clc
%% 统计描述
MIN = min(Test); % 每一列的最小值
MAX = max(Test); % 每一列的最大值
MEAN = mean(Test); % 每一列的均值
MEDIAN = median(Test); %每一列的中位数
SKEWNESS = skewness(Test); %每一列的偏度
KURTOSIS = kurtosis(Test); %每一列的峰度
STD = std(Test); % 每一列的标准差
RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD] %将这些统计量放到一个矩阵中表示二、皮尔逊相关系数
2.1注意事项

 简单来说,就是在进行皮尔逊相关系数之前需要绘制这两个变量的散点图查看是否为线性关系,若是就用皮尔逊,若不是就用斯皮尔曼。
简单来说,就是在进行皮尔逊相关系数之前需要绘制这两个变量的散点图查看是否为线性关系,若是就用皮尔逊,若不是就用斯皮尔曼。

上图为一般情况下相关系数的解释,实际可根据题目背景解释即可,只要言之有理即可。
2.2 SPSS绘制散点图
以这个数据为例:

这里使用Spss比较方便: 导入数据 - 图形 - 旧对话框 - 散点图/点图 - 矩阵散点图 - 将指标拖入矩阵变量(M)- 确定

这里用高版本的绘制(我用的27)感觉好看一点,如下:

注意:在得到变量之间为线性关系的时候才能继续下面的计算步骤。
2.3 MATLAB计算皮尔逊相关系数
2.3.1 MATLAB计算皮尔逊相关系数
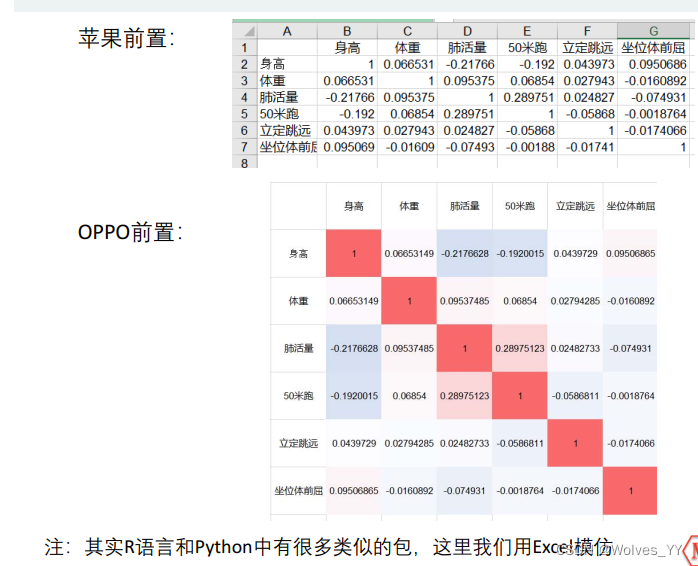
R = corrcoef(Test) % correlation coefficient
得到的R即为相关系数矩阵,其中1为自己和自己的相关性,自然为1,0.0665为第一列和第二列的相关系数,-0.2177为第一列和第三列的相关系数,0.0954为第一列和第三列的相关系数,其他的以此类推。
2.3.2 相关系数矩阵的美化
关于这里的美化,具体操作看该系列第一个视频38分钟左右处。

2.4 对皮尔逊相关系数进行假设检验(p值判断法)
2.4.1 假设检验


![]()
简单来说,就是当算出来的p值<0.01,<.05,<0.10的情况下,即在90%,95%,99%的置信水平上,拒绝原假设r = 0,因此r是显著的不为0的。(实际做的时候,就把假设和备择假设写上,然后算出p值,接着就把这段话写下来)
2.4.2 MATLAB和SPSS计算p值
①MATLAB计算p值

%% 计算各列之间的相关系数以及p值
[R,P] = corrcoef(Test)
% 在EXCEL表格中给数据右上角标上显著性符号吧
P < 0.01 % 标记3颗星的位置
(P < 0.05) .* (P > 0.01) % 标记2颗星的位置
(P < 0.1) .* (P > 0.05) % % 标记1颗星的位置但是MATLAB计算出来的p值放在Excle里,不好标记*,所以可以采用Spss。
②spss计算p值
SPSS里 分析 - 相关 - 双变量- 把变量托到右边 - 确定 。结果如下图,和matlab的结果一样:

2.5 正态分布检验
2.5.1 JB检验(大样本n > 30)


% 用循环检验所有列的数据
n_c = size(Test,2); % number of column 数据的列数
H = zeros(1,6); % 初始化节省时间和消耗
P = zeros(1,6);
for i = 1:n_c
[h,p] = jbtest(Test(:,i),0.05);
H(i)=h;
P(i)=p;
end
disp(H)
disp(P)代码里的6是因为这里的数据变量有6个,0.05代表现在是95%的置信水平,实际中可根据需要自行调整。输出的H为1就是在95%的置信水平下拒绝原假设,即不服从正态分布,0则是不拒绝原假设,即服从正态分布;P则是p值。
2.5.2 Shapiro-wilk检验(小样本 3 ≤ n ≤ 50)

结果如下:

只需要看最后一列即可,都小于0.01,说明在99%的置信水平下,拒绝原假设,即不服从正态分布。
2.5.3 QQ图
要求样本量非常大,不太推荐用QQ图,用前面两个检验即可。

MATLAB画QQ图的命令:
% Q-Q图
qqplot(Test(:,1))二、斯皮尔曼相关系数
2.1 斯皮尔曼相关系数
第一种定义:
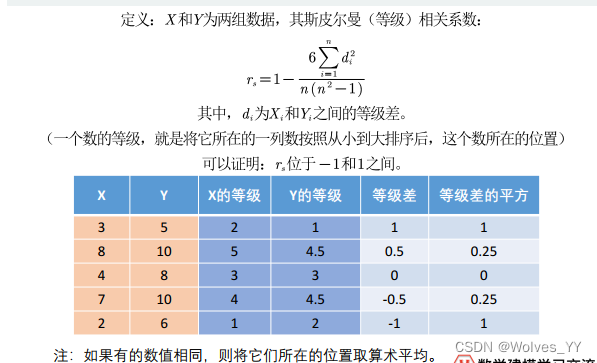

第二种定义:

2.2 斯皮尔曼相关系数的计算

第一种为只有两个变量时使用,第二种为有多个变量时使用。
2.3 两种相关系数结果的对比

2.4 对斯皮尔曼相关系数进行假设检验(p值判断法)
小样本情况下:

大样本情况下:

①matlab计算P值

②SPSS计算p值
SPSS里 分析 - 相关 - 双变量- 把变量托到右边 - 勾选上斯皮尔曼 - 确定 。
结果如下,和MATLAB结果一样的:

三、两个相关系数系数的比较

总结下来就是:
用相关系数前,先对数据进行描述性统计,然后画散点图看数据是否是线性的,接着对数据做正态性检验,满足正态性检验后再计算皮尔逊相关系数并看是不是显著的。(进行假设检验的前提是通过正态分布检验)
如果没有通过检验则用斯皮尔曼相关系数。