线性规划案例分享

news2024/11/27 22:37:37

今天想写一个最优传输的简单实现，结果学歪了，学到线性规划去了，这里我发现了一个宝藏网站
虽然是讲计量经济的，但是里面提供的公式和代码我很喜欢，有时间可以好好读一下
https://python.quantecon.org/lp_intro.html

参考博客
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html

https://python.quantecon.org/lp_intro.html

example1

在这里插入图片描述

图解法

import numpy as np
from scipy.optimize import linprog
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon

fig, ax = plt.subplots(figsize=(8, 6))
ax.grid()

# Draw constraint lines
ax.hlines(0, -1, 17.5)
ax.vlines(0, -1, 12)
ax.plot(np.linspace(-1, 17.5, 100), 6-0.4*np.linspace(-1, 17.5, 100), color="c")## 画一条直线
ax.plot(np.linspace(-1, 5.5, 100), 10-2*np.linspace(-1, 5.5, 100), color="c") ## 画一条直线
ax.text(1.5, 8, "$2x_1 + 5x_2 \leq 30$", size=12)
ax.text(10, 2.5, "$4x_1 + 2x_2 \leq 20$", size=12)
ax.text(-2, 2, "$x_2 \geq 0$", size=12)
ax.text(2.5, -0.7, "$x_1 \geq 0$", size=12)

# Draw the feasible region
feasible_set = Polygon(np.array([[0, 0],
                                 [0, 6],
                                 [2.5, 5],
                                 [5, 0]]),
                       color="cyan")
ax.add_patch(feasible_set)

# Draw the objective function
ax.plot(np.linspace(-1, 5.5, 100), 3.875-0.75*np.linspace(-1, 5.5, 100), color="orange")
ax.plot(np.linspace(-1, 5.5, 100), 5.375-0.75*np.linspace(-1, 5.5, 100), color="orange")
ax.plot(np.linspace(-1, 5.5, 100), 6.875-0.75*np.linspace(-1, 5.5, 100), color="orange")
ax.arrow(-1.6, 5, 0, 2, width = 0.05, head_width=0.2, head_length=0.5, color="orange")
ax.text(5.7, 1, "$z = 3x_1 + 4x_2$", size=12)

# Draw the optimal solution
ax.plot(2.5, 5, "*", color="black")
ax.text(2.7, 5.2, "Optimal Solution", size=12)

plt.show()

结果如下，这个图还蛮好看的
在这里插入图片描述

python代码 - solution

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import linprog
from quantecon.optimize.linprog_simplex import linprog_simplex
import ot
from scipy.stats import betabinom
import networkx as nx
# Define parameters

# Construct parameters
c_ex1 = np.array([3, 4])

# Inequality constraints
A_ex1 = np.array([[2, 5],
                  [4, 2]])
b_ex1 = np.array([30,20])

# Solve the problem
# we put a negative sign on the objective as linprog does minimization
res_ex1 = linprog(-c_ex1, A_ub=A_ex1, b_ub=b_ex1)

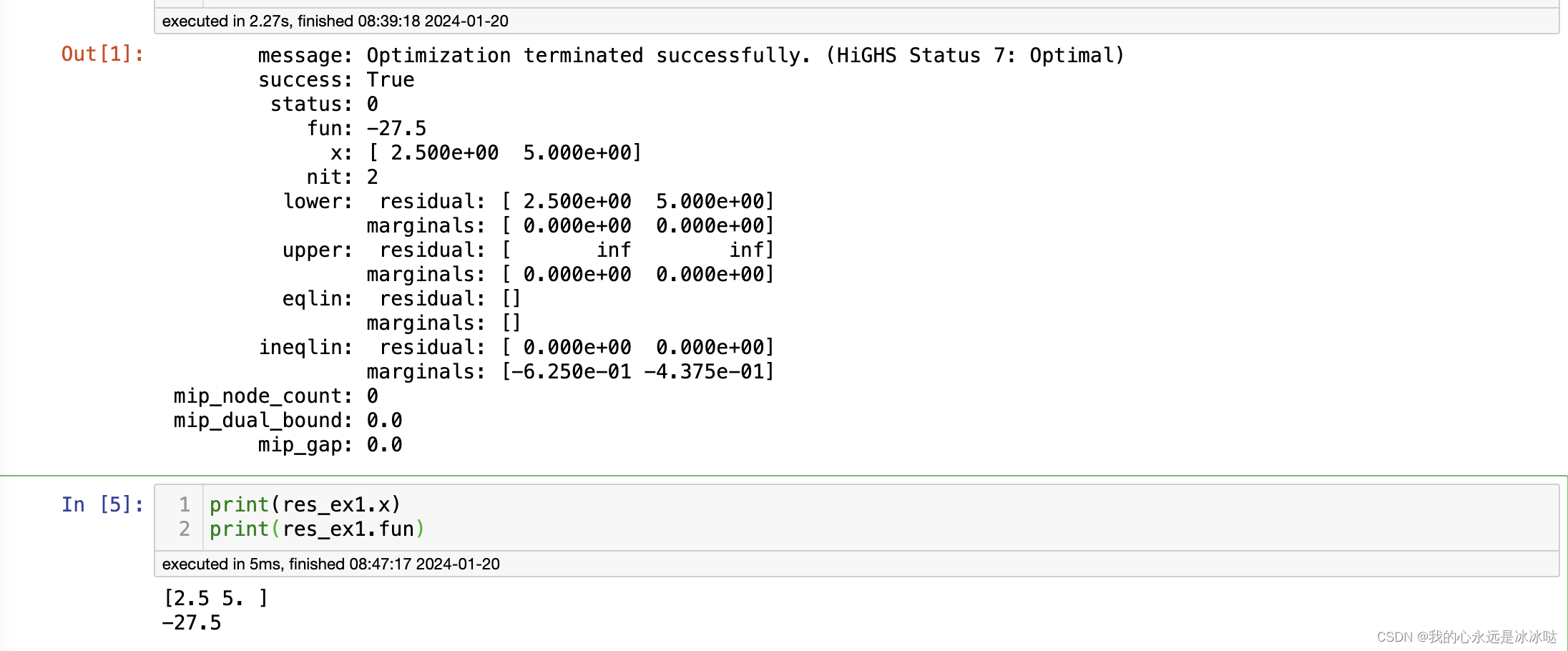
res_ex1

结果如下
在这里插入图片描述

matlab代码-solution

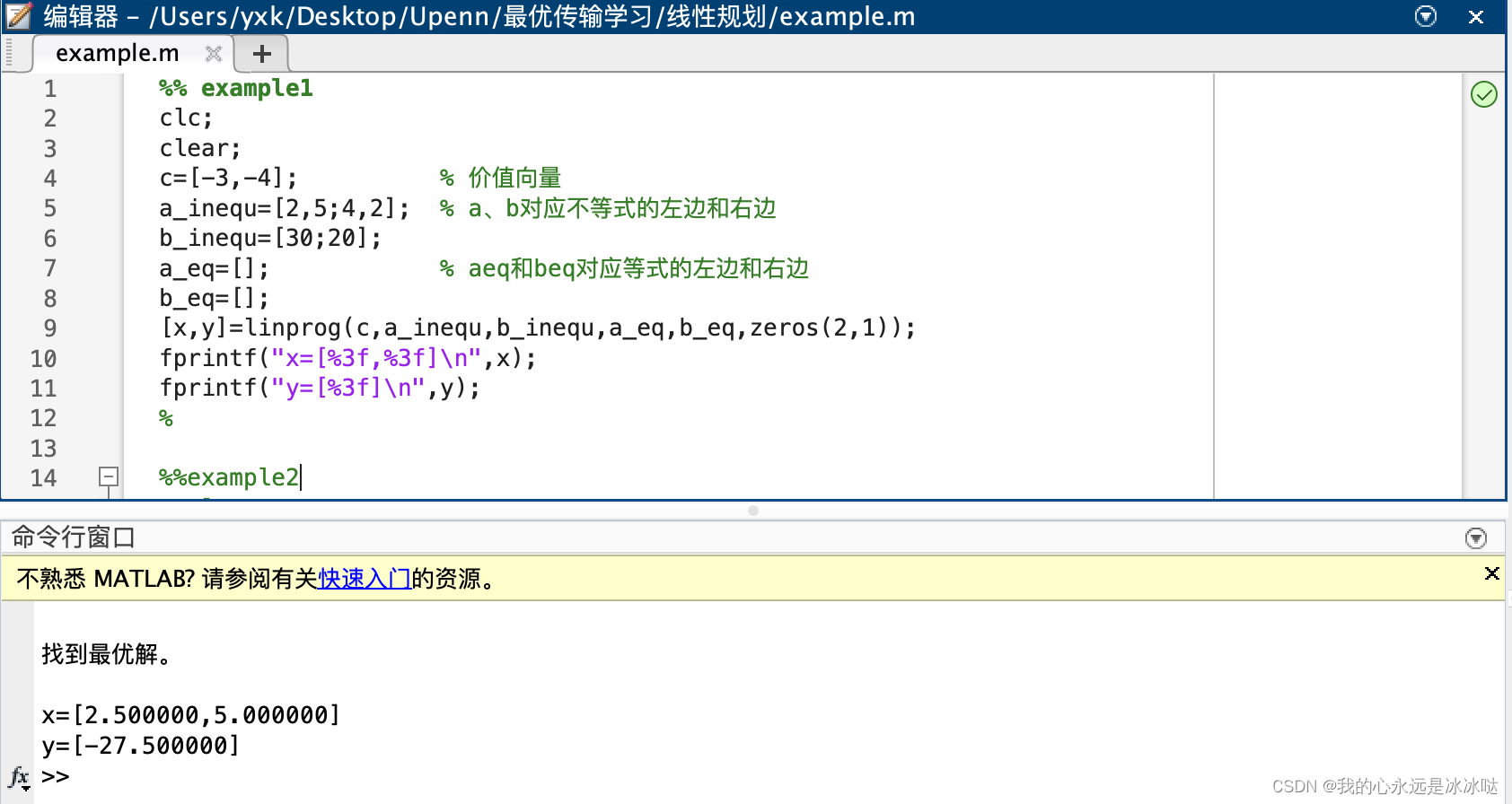
%% example1
clc;
clear;
c=[-3,-4];			% 价值向量
a_inequ=[2,5;4,2];	% a、b对应不等式的左边和右边
b_inequ=[30;20];
a_eq=[];			% aeq和beq对应等式的左边和右边
b_eq=[];
[x,y]=linprog(c,a_inequ,b_inequ,a_eq,b_eq,zeros(2,1));
fprintf("x=[%3f,%3f]\n",x);
fprintf("y=[%3f]\n",y);
%

结果如下
在这里插入图片描述

example2

在这里插入图片描述

python代码

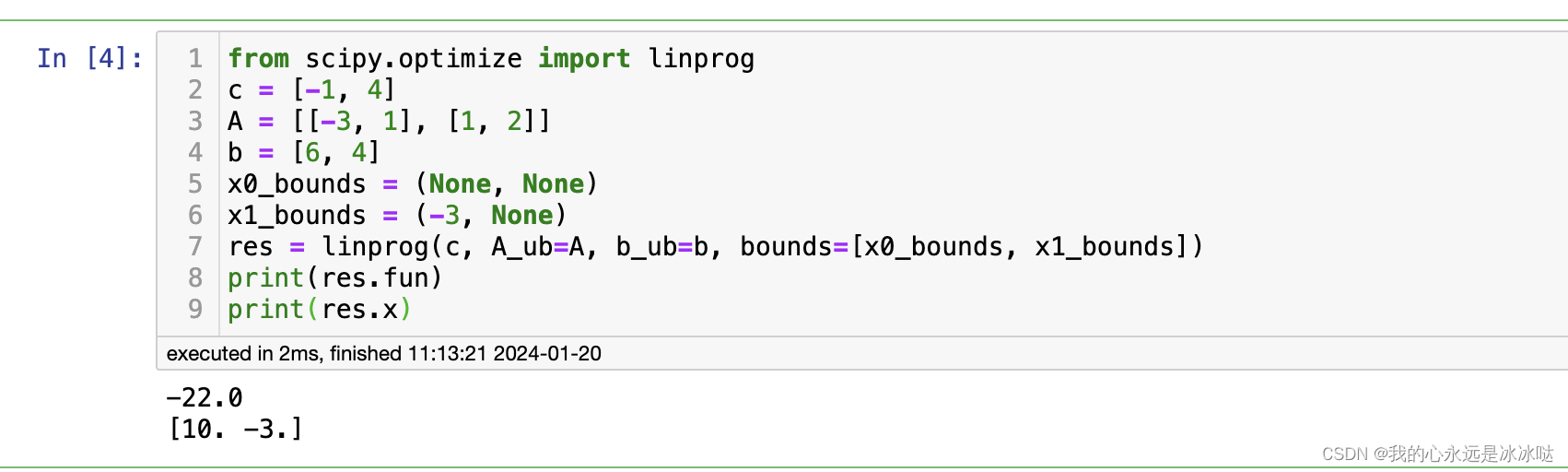
from scipy.optimize import linprog
c = [-1, 4]
A = [[-3, 1], [1, 2]]
b = [6, 4]
x0_bounds = (None, None)
x1_bounds = (-3, None)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds])
print(res.fun)
print(res.x)

结果如下
在这里插入图片描述

matlab代码


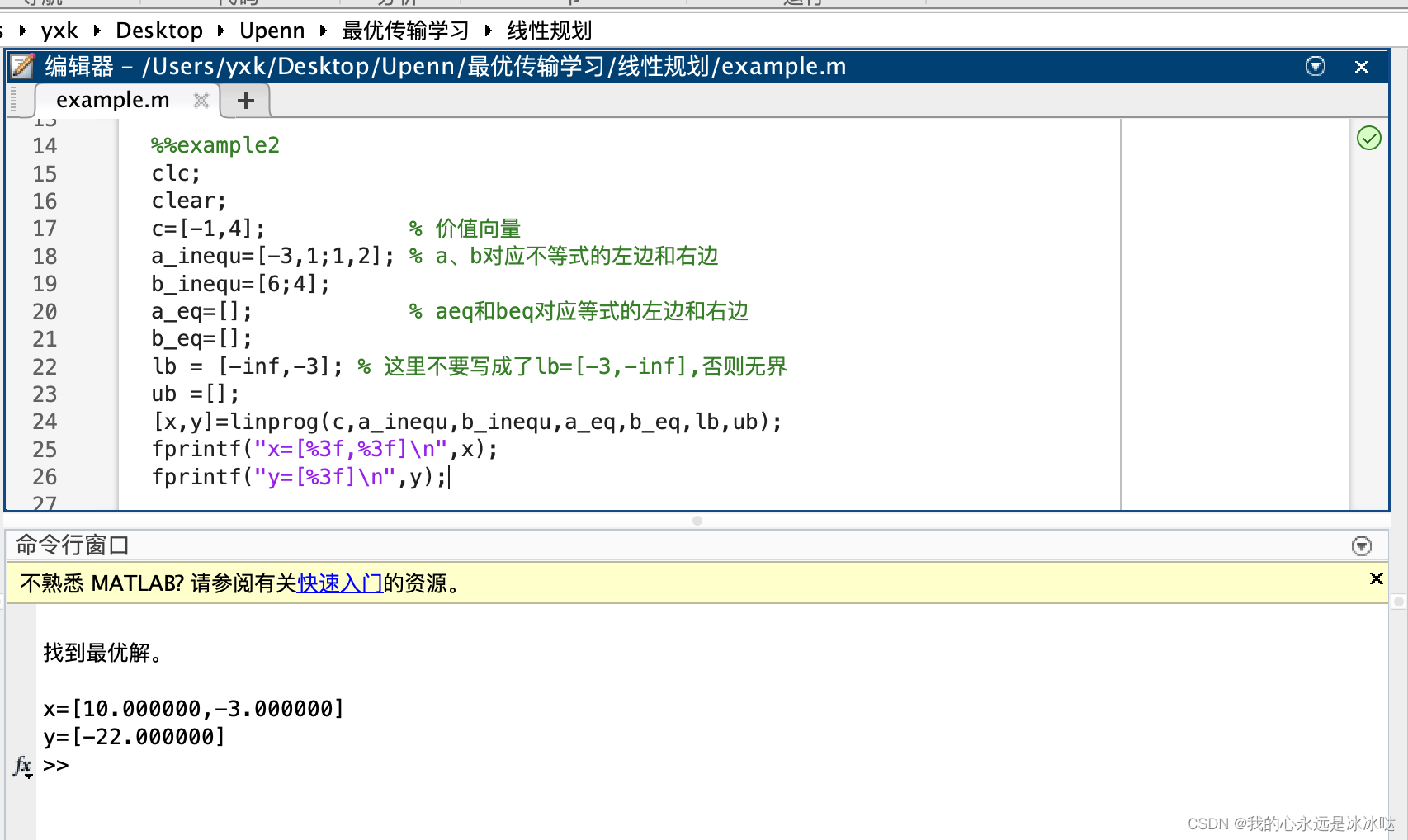
%%example2
clc;
clear;
c=[-1,4];			% 价值向量
a_inequ=[-3,1;1,2];	% a、b对应不等式的左边和右边
b_inequ=[6;4];
a_eq=[];			% aeq和beq对应等式的左边和右边
b_eq=[];
lb = [-inf,-3]; % 这里不要写成了lb=[-3,-inf],否则无界
ub =[];
[x,y]=linprog(c,a_inequ,b_inequ,a_eq,b_eq,lb,ub);
fprintf("x=[%3f,%3f]\n",x);
fprintf("y=[%3f]\n",y);

在这里插入图片描述

example3

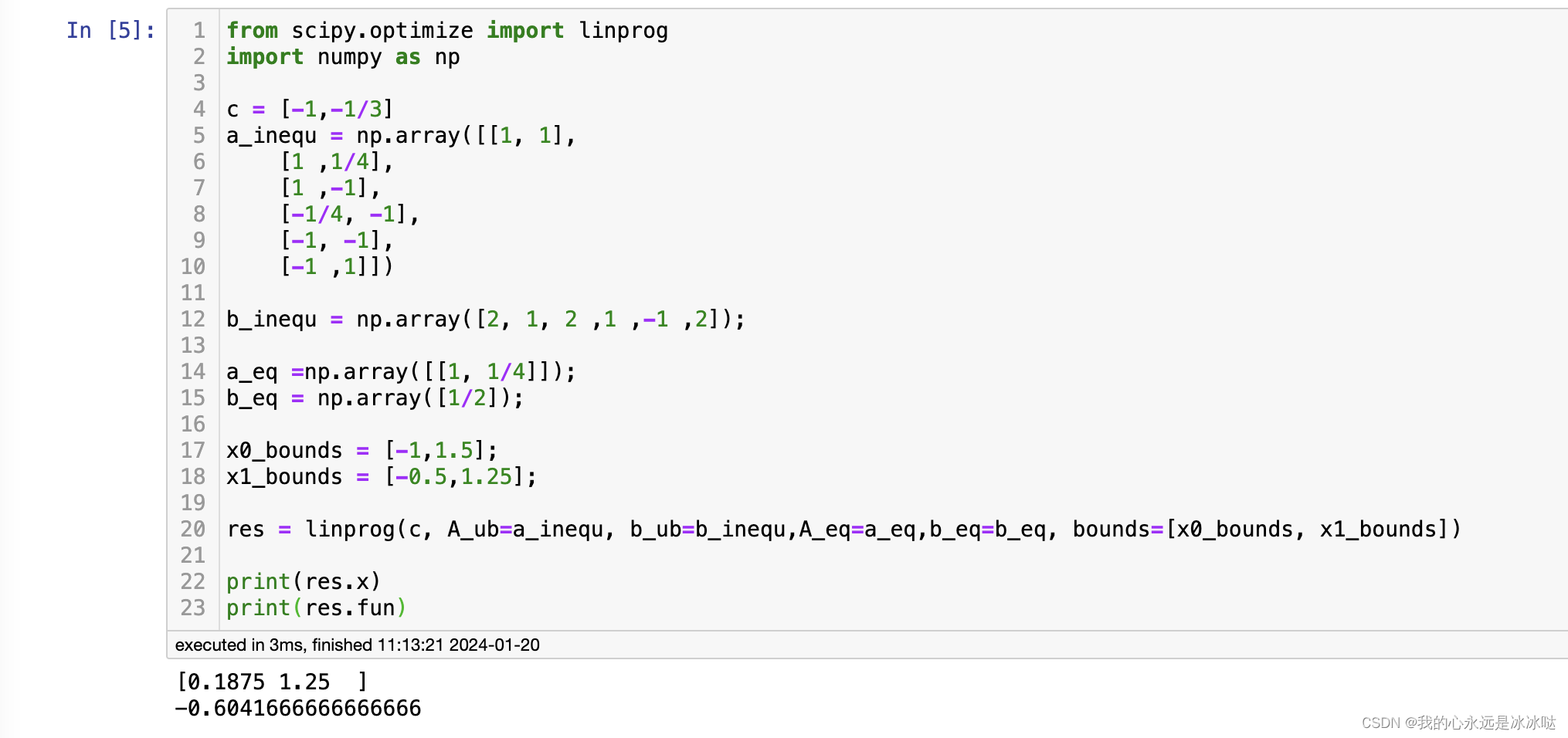
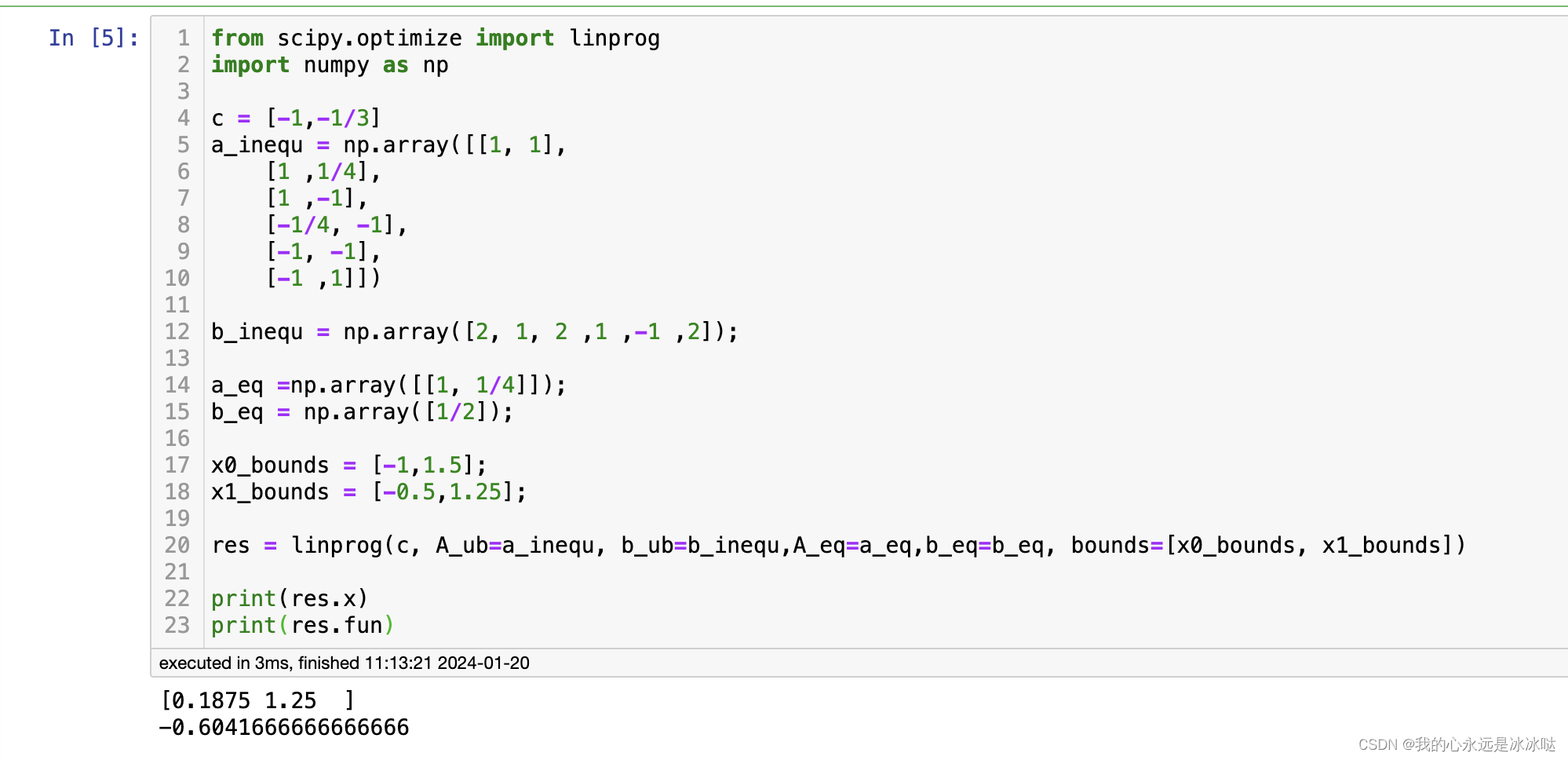
在这里插入图片描述

python代码


from scipy.optimize import linprog
import numpy as np

c = [-1,-1/3]
a_inequ = np.array([[1, 1],
    [1 ,1/4],
    [1 ,-1],
    [-1/4, -1],
    [-1, -1],
    [-1 ,1]])

b_inequ = np.array([2, 1, 2 ,1 ,-1 ,2]);

a_eq =np.array([[1, 1/4]]);
b_eq = np.array([1/2]);

x0_bounds = [-1,1.5];
x1_bounds = [-0.5,1.25];

res = linprog(c, A_ub=a_inequ, b_ub=b_inequ,A_eq=a_eq,b_eq=b_eq, bounds=[x0_bounds, x1_bounds])

print(res.x)
print(res.fun)

结果如下
在这里插入图片描述

matlab代码

clc;
clear;
c = [-1 -1/3];
a_inequ  = [1 1; 1 1/4;
            1 -1; -1/4 -1;
           -1 -1;-1 1];
b_inequ = [2 1 2 1 -1 2];
a_eq = [1 1/4];
b_eq = 1/2;
lb = [-1,-0.5];
ub = [1.5,1.25];
[x,y] = linprog(c,a_inequ,b_inequ,a_eq,b_eq,lb,ub);
fprintf("x=[%3f,%3f]\n",x);
fprintf("y=[%3f]\n",y);

在这里插入图片描述嘿嘿，先到这里吧