【排序算法】六、快速排序（C/C++）

news2025/1/13 14:03:58

「前言」文章内容是排序算法之快速排序的讲解。（所有文章已经分类好，放心食用）

「归属专栏」排序算法

「主页链接」个人主页

「笔者」枫叶先生(fy)

目录

  • 快速排序
    • 1.1 原理
    • 1.2 Hoare版本（单趟）
    • 1.3 快速排序完整代码（Hoare版）(递归实现)
    • 1.4 选择基准数key优化（三数取中）
    • 1.5 挖坑法（单趟）
    • 1.6 快速排序完整代码（挖坑法）(递归实现)
    • 1.7 前后指针版（单趟）
    • 1.8 快速排序完整代码（前后指针版）(递归实现)
    • 1.9 快速排序小区间优化
    • 1.9 快速排序非递归实现
    • 1.10 特性总结

快速排序

1.1 原理

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，一种高效的排序算法

基本思想：是通过一趟排序将待排序的数据分割成独立的两部分，其中一部分的所有数据都比另一部分小，然后再按照此方法对这两部分数据分别进行快速排序，以达到整个数据变成有序序列

具体步骤如下：

  1. 从数列中挑出一个元素作为基准元素
  2. 将比基准元素小的元素放在其左边，比基准元素大的元素放在其右边，基准元素所在位置即为最终位置
  3. 分别对左右两个子序列递归地进行快速排序

对于如何按照基准值将待排序列分为两个子序列（单趟），单趟常见的方式有：

  1. Hoare版本
  2. 挖坑法
  3. 前后指针法

下面先谈Hoare版本的

1.2 Hoare版本（单趟）

Hoare版本的单趟排序的动图如下：
在这里插入图片描述

Hoare版本的单趟排序的基本步骤如下：

  1. 从数组中选出一个key，一般是最左边或是最右边的，上面动图是选左边的
  2. 定义一个left: L和一个right: R。如果选的key是左边的，则需要R先走，然后L从左向右走，R从右向左走。（注意：若选择最右边的数据作为key，则需要L先走）
  3. 选左：
  4. 选取最左边的基准值作为key，L和R的任务：（1）L：找比key大的；（2）R：找比key小的
  5. 选取最左边的基准值作为key： 在走的过程中，若R遇到小于key的数，则停下，L开始走，直到L遇到一个大于key的数时，将L和R的内容交换，R再次开始走，如此进行下去，直到L和R最终相遇，相遇结束。此时将相遇点的内容与key交换即可
  6. 选右：
  7. 选取最左边的基准值作为key，L和R的任务：（1）L：找比key小的；（2）R：找比key大的
  8. 选取最右边的基准值作为key： 在走的过程中，若L遇到小于key的数，则停下，R开始走，直到R遇到一个大于key的数时，将L和R的内容交换，L再次开始走，如此进行下去，直到L和R最终相遇，相遇结束。此时将相遇点的内容与key交换即可

经过一次单趟排序，最终使得key左边的数据全部都小于key，key右边的数据全部都大于key，并且key所在的位置就是最终的位置

相遇位置的值如何保证比key小，相遇点直接和key交换会不会出错，会不会把较大的值换到了左边？

  • 如果选取最左边的基准值作为key，R先走保证相遇位置的值保证比key小
  • 如果R停下来，L走，L撞到R（相遇），相遇位置的值必定比key小
  • 如果L停下来，R走，R撞到L（相遇），相遇位置的值必定比key小
  • 同理，如果选取最右边的基准值作为key，L先走保证相遇位置的值保证比key大

1.3 快速排序完整代码（Hoare版）(递归实现)

首先经过一次单趟排序，然后将key的左序列和右序列再次进行这种单趟排序，如此反复操作下去，直到左右序列只有一个数据，或是左右序列不存在时，停止操作，此时序列（或者子序列）已经有序

排序步骤演示：

类似于二叉树的前序遍历
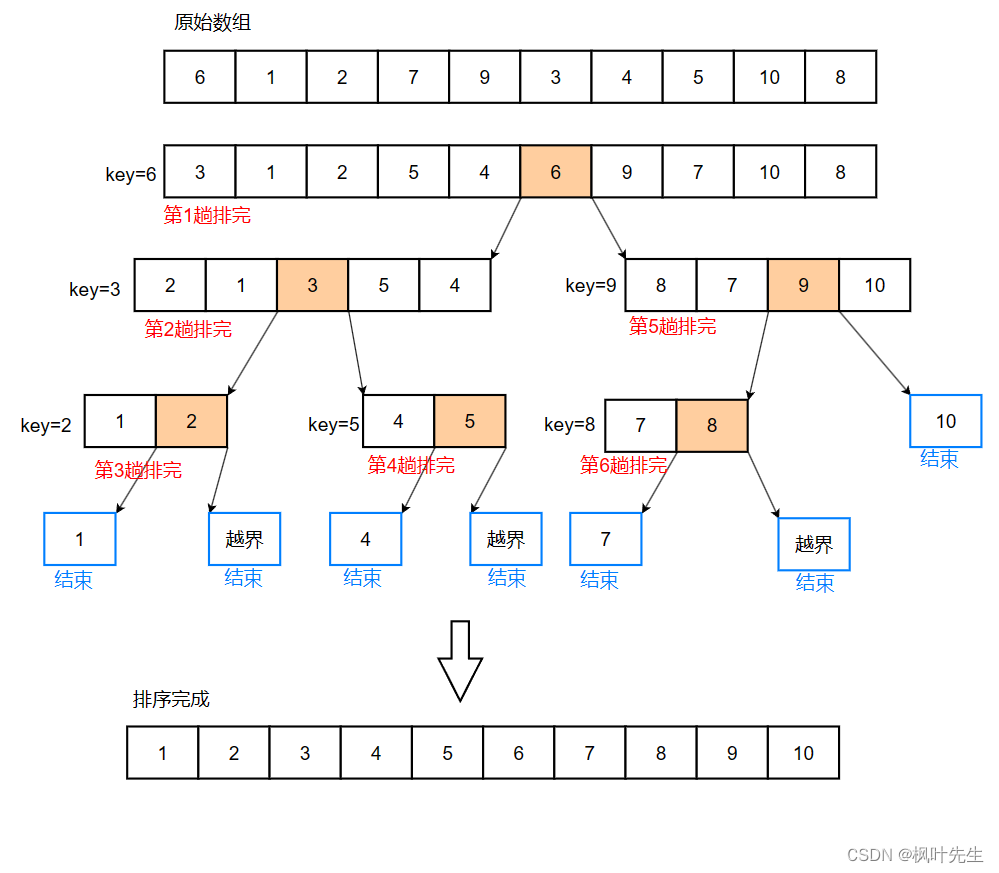
在这里插入图片描述
代码如下（递归，Hoare版）：（升序）

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

// Hoare版本（单趟）
int PartQuickSort(int* arr, int left, int right)
{
	int keyi = left; // key的下标，选左边为key
	while (left < right) // left == right即相遇
	{
		// right先走，找比key小的值
		while (left < right && arr[right] >= arr[keyi])
		{
			--right;
		}
		// left后走，找比key大的值
		while (left < right && arr[left] <= arr[keyi])
		{
			++left;
		}
		// 找到一组值，交换：交换arr[left] 和 arr[right]
		if (left < right)
		{
			Swap(&arr[left], &arr[right]);
		}
	}
	Swap(&arr[keyi], &arr[left]); // 交换 keyi 和相遇点位置的值，left==right
	return left; // 返回相遇点的下标
}

// 快速排序
void QuickSort(int* arr, int left, int right)
{
	// 1、区间不存在(left > right) 2、只有一个数数不需要再处理(left == right)
	if (left >= right)
	{
		return;
	}

	// 单趟排序并获取基准值
	int keyi = PartQuickSort(arr, left, right);

	// 递归处理每一个子序列（左、右）
	QuickSort(arr, left , keyi - 1); // keyi 左序列进行排序
	QuickSort(arr, keyi + 1, right); // keyi 右序列进行排序
}

1.4 选择基准数key优化（三数取中）

快速排序的时间复杂度是O(NlogN)，是我们在理想情况下计算的结果

在理想情况下，我们每次进行完单趟排序后，key的左序列与右序列的长度都相同
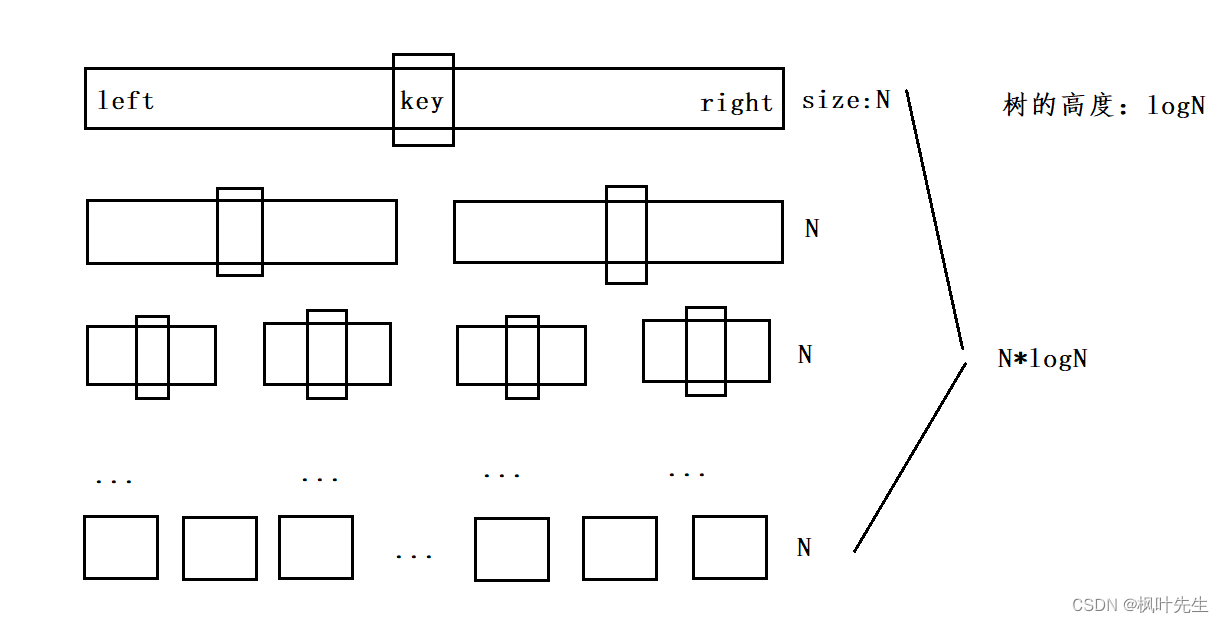
在这里插入图片描述
若每趟排序所选的key都正好是该序列的中间值，即单趟排序结束后key位于序列正中间，那么快速排序的时间复杂度就是O(NlogN)

可是谁能保证你每次选取的key都是正中间的那个数呢？

例如，以下数组：
在这里插入图片描述
如果基准值key是数组中最大或最小的数值（假设选左边），则快速排序的递归深度会非常深，排序效率会很低

若是一个有序数组使用快速排序，这种情况下，快速排序的时间复杂度退化为O(N^2)
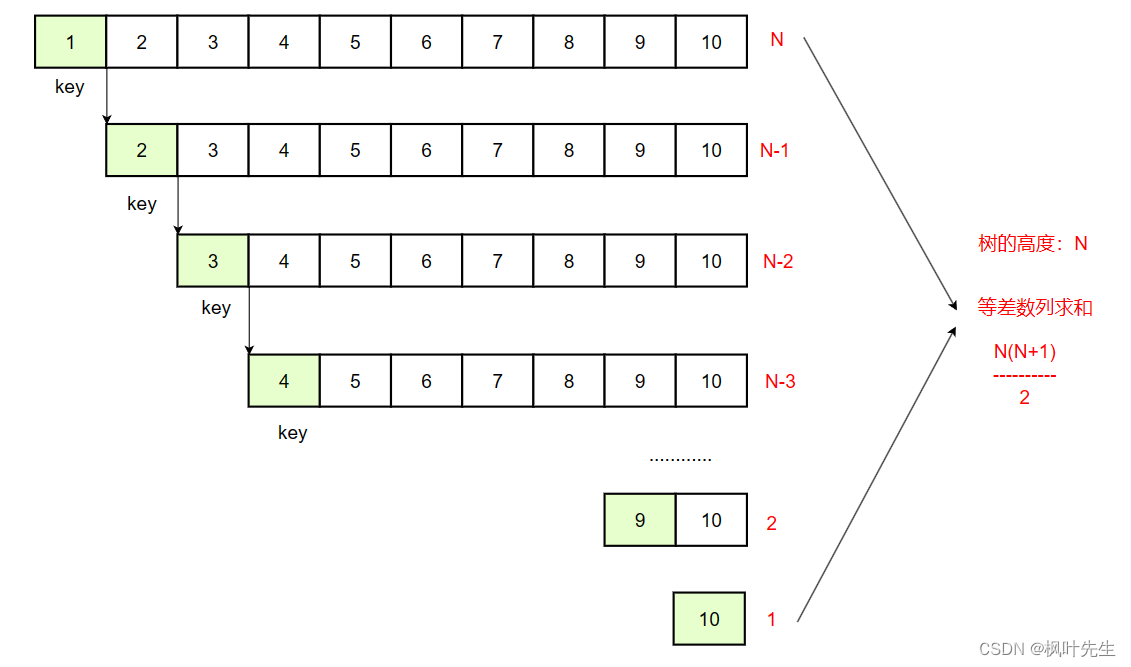
在这里插入图片描述
对快速排序效率影响最大的就是选取的key，若选取的key越接近中间位置，则则效率越高

为了避免这种极端情况的发生，于是出现了三数取中

三数取中

三数取中的方法是从待排序数组中选择三个元素，分别是左端、右端和中间位置的元素，然后取这三个元素的中间值作为基准元素

代码如下：

// 三数取中
int GetMidIndex(int* arr, int left, int right)
{
	int mid = left + (right - left) / 2;
	if (arr[left] < arr[mid]) 
	{
		if (arr[mid] < arr[right]) 
		{
			return mid; // [mid]是中间值
		}
		else if (arr[left] > arr[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else  // arr[left] >= arr[mid]
	{
		if (arr[mid] > arr[right])
		{
			return mid;
		}
		else if (arr[left] < arr[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

需要注意，当大小居中的数不在序列的最左或是最右端时，我们不是就以居中数的位置作为key的位置，而是将key的值与最左端的值进行交换，这样key就还是位于最左端了，所写代码就无需改变，而只需在单趟排序代码开头加上以下两句代码即可:

如下：

// Hoare版本（单趟）
int PartQuickSort(int* arr, int left, int right)
{
	// 三数取中
	int midi = GetMidIndex(arr, left, right);
	Swap(&arr[left], &arr[midi]);

	int keyi = left; // key的下标，选左边为key
	// ...
	return left; // 返回相遇点的下标
}

1.5 挖坑法（单趟）

挖坑法是基于Hoare版本改良的（Hoare版本代码细节太多）

挖坑法的单趟排序的动图如下：
在这里插入图片描述
挖坑法的单趟排序的基本步骤如下：

  1. 选出一个数据（上图选最左为坑）存放在key变量中，在该数据位置形成一个坑
  2. 定义一个left: L和一个right: R，L从左向右走，R从右向左走（若在最左边挖坑，则需要R先走；若在最右边挖坑，则需要L先走）
  3. 选取最左边的作为坑位为例：
  4. L和R的任务：（1）L：找比key大的；（2）R：找比key小的
  5. R先走，在走的过程中，若R遇到小于key的数，则将该数抛入坑位，并在此处形成一个新的坑位，这时L再向后走，若遇到大于key的数，则将其抛入坑位，又形成一个坑位，如此循环下去，直到最终L和R相遇，这时将key抛入坑位即可

经过一次单趟排序，最终也使得key左边的数据全部都小于key，key右边的数据全部都大于key，并且key所在的位置就是最终的位置

挖坑法代码如下：（升序）

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

// 挖坑法（单趟）
int PartQuickSort2(int* arr, int left, int right)
{
	// 三数取中
	int midi = GetMidIndex(arr, left, right);
	Swap(&arr[left], &arr[midi]);
	
	int key = arr[left]; // 在最左形成一个坑位
	int hole = left; // 坑的下标
	while (left < right)
	{
		// right先走，找比key小的
		while (left < right && arr[right] >= key)
		{
			--right;
		}
		arr[hole] = arr[right]; // 填坑
		hole = right;
		// left后走，找比key大的
		while (left < right && arr[left] <= key)
		{
			++left;
		}
		arr[hole] = arr[left]; // 填坑
		hole = left;
	}
	arr[hole] = key;
	return hole;
}

1.6 快速排序完整代码（挖坑法）(递归实现)

代码如下（递归，挖坑法）：（升序）

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

// 挖坑法（单趟）
int PartQuickSort2(int* arr, int left, int right)
{
	// 三数取中
	int midi = GetMidIndex(arr, left, right);
	Swap(&arr[left], &arr[midi]);
	
	int key = arr[left]; // 在最左形成一个坑位
	int hole = left; // 坑的下标
	while (left < right)
	{
		// right先走，找比key小的
		while (left < right && arr[right] >= key)
		{
			--right;
		}
		arr[hole] = arr[right]; // 填坑
		hole = right;
		// left后走，找比key大的
		while (left < right && arr[left] <= key)
		{
			++left;
		}
		arr[hole] = arr[left]; // 填坑
		hole = left;
	}
	arr[hole] = key;
	return hole; // 返回key的下标
}

// 快速排序
void QuickSort(int* arr, int left, int right)
{
	// 1、区间不存在(left > right) 2、只有一个数数不需要再处理(left == right)
	if (left >= right)
	{
		return;
	}

	// 单趟排序并获取基准值
	int keyi = PartQuickSort2(arr, left, right);

	// 递归处理每一个子序列（左、右）
	QuickSort(arr, left , keyi - 1); // keyi 左序列进行排序
	QuickSort(arr, keyi + 1, right); // keyi 右序列进行排序
}

1.7 前后指针版（单趟）

前后指针版的单趟排序的动图如下：
在这里插入图片描述
前后指针法的单趟排序的基本步骤如下：

  1. 选出一个key，最左边或是最右边的（上图选最左）
  2. 开始时，prev指向序列的左边，cur指向prev+1的位置
  3. 情况1：若cur指向的内容小于key，则prev向右后移动一位，然后交换prev和cur指针指向的内容，然后cur指针++
  4. 情况2：若cur指向的内容大于key，则cur指针直接++。如此进行下去，直到cur指针越界，此时将key和prev指针指向的内容交换即可

前后指针版代码如下：（升序）

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

// 前后指针版（单趟）
int PartQuickSort3(int* arr, int left, int right)
{
	// 三数取中
	int midi = GetMidIndex(arr, left, right);
	Swap(&arr[left], &arr[midi]);

	int keyi = left;
	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
		if (arr[cur] < arr[keyi]) // cur指向的内容小于key
		{
			++prev;
			if(prev != cur)
				Swap(&arr[prev], &arr[cur]);
		}
		++cur;
	}
	Swap(&arr[keyi], &arr[prev]);
	return prev; // 返回key当前的下标
}

1.8 快速排序完整代码（前后指针版）(递归实现)

代码如下（递归，前后指针版）：（升序）

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

// 前后指针版（单趟）
int PartQuickSort3(int* arr, int left, int right)
{
	// 三数取中
	int midi = GetMidIndex(arr, left, right);
	Swap(&arr[left], &arr[midi]);

	int keyi = left;
	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
		if (arr[cur] < arr[keyi]) // cur指向的内容小于key
		{
			++prev;
			if(prev != cur)
				Swap(&arr[prev], &arr[cur]);
		}
		++cur;
	}
	Swap(&arr[keyi], &arr[prev]);
	return prev; // 返回key当前的下标
}

// 快速排序
void QuickSort(int* arr, int left, int right)
{
	// 1、区间不存在(left > right) 2、只有一个数数不需要再处理(left == right)
	if (left >= right)
	{
		return;
	}

	// 单趟排序并获取基准值
	int keyi = PartQuickSort3(arr, left, right);

	// 递归处理每一个子序列（左、右）
	QuickSort(arr, left , keyi - 1); // keyi 左序列进行排序
	QuickSort(arr, keyi + 1, right); // keyi 右序列进行排序
}

1.9 快速排序小区间优化

快速排序的递归类似于二叉树的形式，深度越深待排数组的长度越短，但是数量也越多，调用函数的次数就越多，开辟函数栈帧的消耗越大，导致效率下降（每一层的递归次数会以2倍的形式快速增长，后三层的递归次数占据了总递归次数的70%以上）

优化的方式就是设置一个排序序列的长度大小，若是数组长度大于这个指定的数，则调用快速排序，若是数组长度小于这个指定的数，不再调用快速排序，而是调用插入排序或者其他排序

这个数可自行调整，代码如下：

// 快速排序（优化）
void QuickSort2(int* arr, int left, int right)
{
	// 1、区间不存在(left > right) 2、只有一个数数不需要再处理(left == right)
	if (left >= right)
	{
		return;
	}

	if (right - left + 1 > 8) // 可自行调整
	{
		// 单趟排序并获取基准值
		int keyi = PartQuickSort3(arr, left, right);
		// 递归处理每一个子序列（左、右）
		QuickSort(arr, left, keyi - 1); // keyi 左序列进行排序
		QuickSort(arr, keyi + 1, right); // keyi 右序列进行排序
	}
	else // 调用其他排序
	{
		InsertSort(arr + left, right - left + 1);
	}
}

1.9 快速排序非递归实现

将一个用递归实现的算法改为非递归时，一般需要借用一个数据结构，那就是栈

C语言的库没有封装有stack，需要自己手搓一个，C++的STL库则封装有

如果是C语言，我就不贴代码了，代码链接：stack，下面简单介绍一下手搓stack的接口

// 初始化
void StackInit(ST* ps);
// 销毁栈
void StackDestroy(ST* ps);
// 入栈
void StackPush(ST* ps, STDataType x);
// 出栈
void StackPop(ST* ps);
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0
bool StackEmpty(ST* ps);
// 获取栈顶元素
STDataType StackTop(ST* ps);
// 获取栈中有效元素个数
int StackSize(ST* ps);

快速排序的非递归算法基本思路：

  1. 先将待排序列的第一个元素的下标和最后一个元素的下标入栈
  2. 当栈不为空时，读取栈中的信息（一次读取两个：一个是left，另一个是right），然后调用某一版本的单趟排序，排完后获得了key的下标，然后判断key的左序列和右序列是否还需要排序，若还需要排序，就将相应序列的left和right入栈；若不需排序了（序列只有一个元素或是区间不存在），就不需要将该序列区间的信息入栈
  3. 重复执行步骤2，直到栈为空为止

C语言代码如下：（升序）

void QuickSort3(int* arr, int left, int right)
{
	Stack st; // 创建栈
	StackInit(&st); // 初始化栈
	StackPush(&st, left); // 待排序列的left
	StackPush(&st, right); // 待排序列的right

	while (!StackEmpty(&st)) // 栈为空结束
	{
		int right = StackTop(&st); // 读取right
		StackPop(&st); // 出栈
		int left = StackTop(&st); // 读取left
		StackPop(&st); // 出栈

		// 判断左右区间是否合理，若不合理则跳过本次循环
		if (left >= right)
		{
			continue;
		}
	
		int keyi = PartQuickSort2(arr, left, right); // 调用单趟的方法

		StackPush(&st, left); // 左序列的left入栈
		StackPush(&st, keyi - 1); // 左序列的right入栈
		
		StackPush(&st, keyi + 1); // 右序列的left入栈
		StackPush(&st, right); // 右序列的right入栈
	}
}

C++代码如下：（升序）

void QuickSort4(int* arr, int left, int right)
{
	stack<int> st; // 创建栈
	st.push(left); // 待排序列的left
	st.push(right); // 待排序列的right

	while (!st.empty()) // 栈为空结束
	{
		int right = st.top(); // 读取right
		st.pop(); // 出栈
		int left = st.top(); // 读取left
		st.pop(); //出栈

		//判断左右区间是否合理，若不合理则跳过本次循环
		if (left >= right)
		{
			continue;
		}

		int keyi = PartQuickSort2(arr, left, right); // 调用单趟的方法

		st.push(left); // 左序列的left入栈
		st.push(keyi - 1); // 左序列的right入栈

		st.push(keyi + 1); // 右序列的left入栈
		st.push(right); // 右序列的right入栈
	}
}

1.10 特性总结

快速排序的特性总结如下：

  • 时间复杂度：平均情况下，快速排序的时间复杂度为O(nlogn)
  • 空间复杂度：O(1)
  • 稳定性：不稳定
  • 不适用于小规模数据，适用于大规模数据的排序

--------------------- END ----------------------

「 作者 」 枫叶先生
「 更新 」 2024.1.20
「 声明 」 余之才疏学浅，故所撰文疏漏难免，
          或有谬误或不准确之处，敬请读者批评指正。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1399184.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

70.Redis缓存优化实践（基于分类树场景）

70.Redis缓存优化实践（基于分类树场景）

文章目录 前言第一次优化第二次优化第三次优化第四次优化第五次优化 前言 分类树查询功能&#xff0c;在各个业务系统中可以说随处可见&#xff0c;特别是在电商系统中。 而在实际工作中&#xff0c;这样一个分类树查询&#xff0c;我们都不断的改进了好几次。这是为什么呢&…
阅读更多...
Lite AD的安装

Lite AD的安装

1、Lite AD的安装及配置 Lite AD流程&#xff1a; &#xff08;1&#xff09;创建一个新的Windows 10&#xff0c;安装tools&#xff0c;再安装ITA组件&#xff08;安装Lite AD会自动安装VAG/VLB&#xff09; &#xff08;2&#xff09;创建一个新的Windows 10&#xff0c;安…
阅读更多...
【GNN报告】“青源Talk”-图可信学习与图大模型研究进展

【GNN报告】“青源Talk”-图可信学习与图大模型研究进展

北航王啸-图自监督学习 简介 介绍 浙大杨洋-探索大图模型预训练 总括 介绍 参考 Yang Yang - Zhejiang University dgraph-web DGraph: ALarge-Scale Financial Dataset for Graph Anomaly Detection All in One: Multi-task Prompting for Graph Neural Networks&#xf…
阅读更多...
Spring Boot实现统一异常处理的技术解析

Spring Boot实现统一异常处理的技术解析

引言 在软件开发过程中&#xff0c;异常处理是非常重要的一环。一个好的异常处理机制可以帮助我们更好地定位问题&#xff0c;提高代码的可维护性和稳定性。Spring Boot作为一款轻量级的Java开发框架&#xff0c;提供了一种简单而高效的方式来实现统一异常处理。本文将详细介绍…
阅读更多...
神器yakit之web fuzzer功能

神器yakit之web fuzzer功能

前言 yakit并不像burp一样单独设置爆破模块&#xff0c;但是yakit也是可以爆破的&#xff0c;并且更好用&#xff08;个人感觉&#xff09;。 手工测试场景中需要渗透人员对报文进行反复的发送畸形或者特定的payload进行查看服务器的反馈并以此来进行下一步的判断。 Fuzz标签便…
阅读更多...
动态规划：完全背包问题

动态规划：完全背包问题

本题力扣上没有&#xff0c;是刷的卡码网第52题52. 携带研究材料感兴趣的小伙伴可以去刷一下&#xff0c;是ACM模式。 题目&#xff1a; 题目描述&#xff1a; 小明是一位科学家&#xff0c;他需要参加一场重要的国际科学大会&#xff0c;以展示自己的最新研究成果。他需要带…
阅读更多...
x-cmd pkg | skate - 个人键值对存储工具

x-cmd pkg | skate - 个人键值对存储工具

目录 简介用户首次快速实验指南功能特点竞品和相关作品进一步探索 简介 skate 是个人键值对存储工具&#xff0c;具备数据加密、云端数据备份以及多设备同步等功能。 它由 Charm 团队开发&#xff0c;借用 Charm Cloud 向用户提供一种快捷的方式来保存和检索各种数据&#xf…
阅读更多...
接口测试 02 -- JMeter入门到实战

接口测试 02 -- JMeter入门到实战

前言 JM eter毕竟是做压测的工具&#xff0c;自动化这块还是有缺陷。 如果公司做一些简单的接口自动化&#xff0c;可以考虑使用JMeter快速完成&#xff0c;如果想做完善的接口自动化体系&#xff0c;建议还是基于Python来做。 为什么学习接口测试要先从JMeter开始&#xff1f;…
阅读更多...
VS Code + Python + Selenium 自动化测试基础-01

VS Code + Python + Selenium 自动化测试基础-01

VS Code Python Selenium 自动化测试基础-01 让我们来讲一个故事为什么要写自动化开发前的准备工作牛刀小试开常用的web DriverAPI-定位元素id定位&#xff1a;find_element_by_id()name 定位&#xff1a;find_element_by_name()class 定位&#xff1a;find_element_by_class…
阅读更多...
Oracle SQL Developer执行sql脚本文件

Oracle SQL Developer执行sql脚本文件

文件过于大&#xff0c;无法打开&#xff0c;直接在界面执行。 ①将文件放置到D盘&#xff0c;文件名 daochu5.sql ② 在工具执行SQL界面输入 d:\daochu5.sql;,点击运行按钮运行
阅读更多...
范围运算between...and和空判断

范围运算between...and和空判断

目录 between...and 空判断 Oracle从入门到总裁:https://blog.csdn.net/weixin_67859959/article/details/135209645 between...and between...and的主要功能是用户进行范围查询,语法如下: select 字段 | 数值 between 最小值 and 最大值; 1.查询工资在 1500 ~ 3000 的所…
阅读更多...
基于JavaWeb+SSM+Vue基于微信小程序生鲜云订单零售系统的设计和实现

基于JavaWeb+SSM+Vue基于微信小程序生鲜云订单零售系统的设计和实现

基于JavaWebSSMVue基于微信小程序生鲜云订单零售系统的设计和实现 滑到文末获取源码Lun文目录前言主要技术系统设计功能截图订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 滑到文末获取源码 Lun文目录 目录 1系统概述 1 1.1 研究背景 1 1.2研究目的 1 1.3系统设计…
阅读更多...
逻辑运算

逻辑运算

目录 AND OR NOT Oracle从入门到总裁:https://blog.csdn.net/weixin_67859959/article/details/135209645 逻辑运算可以保证连接多个条件&#xff0c;连接主要使用 AND、OR 、NOT完成 AND 1.查询职位不是办事员&#xff0c;但是工资低于 300 的员工信息 这个范例可以理…
阅读更多...
【GitHub项目推荐--全球首个开源图像识别系统】【转载】

【GitHub项目推荐--全球首个开源图像识别系统】【转载】

你知道人脸识别、商品识别、车辆识别&#xff0c;以图搜图乃至自动驾驶&#xff0c;背后的技术是什么嘛&#xff1f;并不是图像分类、目标检测这些东西&#xff0c;而是综合使用目标检测、图像分类、度量学习、图像检索的【通用图像识别系统】… 度量学习是啥&#xff1f;图像检…
阅读更多...
Postman接口测试高阶——精通Mock Server模拟服务器的创建及使用等

Postman接口测试高阶——精通Mock Server模拟服务器的创建及使用等

文章目录 一、什么是Mock Server二、为什么使用Mock Server四、Mock Server使用场景五、创建Mock Server模拟服务器1.创建Mock Server2.配置Mock Server3.创建Mock Server模拟服务器成功 六、使用Mock Server模拟服务器七、修改Mock Server模拟服务器配置 一、什么是Mock Serve…
阅读更多...
AI跟踪报道第25期-新加坡内哥谈技术-本周AI发展更新-酷炫来袭

AI跟踪报道第25期-新加坡内哥谈技术-本周AI发展更新-酷炫来袭

每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗&#xff1f;订阅我们的简报&#xff0c;深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同&#xff0c;从行业内部的深度分析和实用指南中受益。不要错过这个机会&#xff0c;成为AI领…
阅读更多...
Java毕业设计-基于springboot的学习英语管理系统-第89期

Java毕业设计-基于springboot的学习英语管理系统-第89期

获取源码资料&#xff0c;请移步从戎源码网&#xff1a;从戎源码网_专业的计算机毕业设计网站 项目介绍 基于springbootvue的医院管理系统&#xff1a;前端 vue、bootstrap、coreui&#xff0c;后端 maven、springmvc、spring、mybatis、redis&#xff0c;角色分为管理员、医…
阅读更多...
后台管理系统: sku管理模块

后台管理系统: sku管理模块

完成添加SKU静态组件 完成添加SKU静态组件 点击添加sku&#xff0c;触发回调&#xff0c;场景为2 静态界面完成 <template><div><el-form ref"form" label-width"80px"><el-form-item label"SPU名称"> 海绵宝宝 <…
阅读更多...
用红黑树封装实现map与set

用红黑树封装实现map与set

红黑树 红黑树 &#xff0c;是一种 二叉搜索树 &#xff0c;但 在每个结点上增加一个存储位表示结点的颜色&#xff0c;可以是 Red 或 Black 。 通过对 任何一条从根到叶子的路径上各个结点着色方式的限制&#xff0c;红黑树确保没有一条路 径会比其他路径长出俩倍 &#xff…
阅读更多...
新品发布 | 多通道总线记录仪TLog1004，是你期待的吗？

新品发布 | 多通道总线记录仪TLog1004，是你期待的吗？

新品发布 2024年1月12日&#xff0c;同星智能又发布一款多通道 CAN &#xff08;FD&#xff09;总线、LIN 总线接口logger设备&#xff0c;此款产品在TLog1002基础上进行了升级&#xff0c;同时内置 3 路数字输入和 2 路数字输出&#xff0c;便于多种信号测量和系统集成。可以满…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023