递归、搜索与回溯算法（专题一：递归）

往期文章（希望小伙伴们在看这篇文章之前，看一下往期文章）

（1）递归、搜索与回溯算法（专题零：解释回溯算法中涉及到的名词）【回溯算法入门必看】-CSDN博客

接下来我会用几道题，来让同学们利用我在专题零中提到的递归的宏观思想来解决这些题目。

1. 汉诺塔

2. 合并两个有序链表

3. 反转链表

4. 两两交换链表中的结点

5. 快速幂

解法一暴力循环

解法二不断拆分

解法三利用了二进制的特点

1. 汉诺塔

这道题可以说是递归最经典的题目之一，接下来我们就从这道题入手，重新认识一下递归是什么？

力扣题目链接

解析：

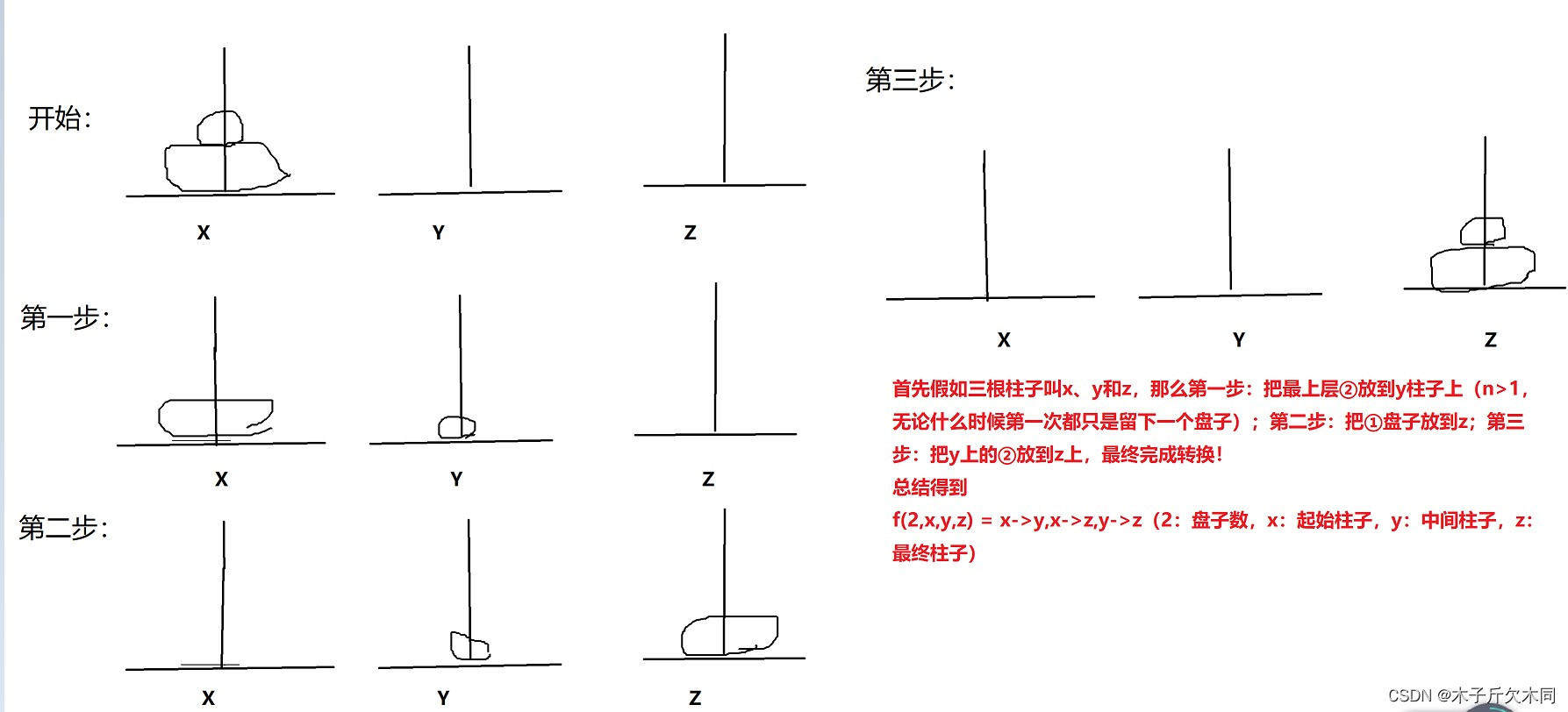
总结：我们想知道n个盘子的次数，记住了，在求解f(n)的时候，我们直接默认f(n - 1)已经完了就可以了！这个在前面已经解释过了，在此不再鳌述。我们将n-1个盘子当作一个整体：这就是类似于分治求解子问题的思想

那么当由3个盘子时，就有公式：f(3,x,y,z) = f(2,x,z,y),x->z,f(2,y,x,z)；当有4个盘子时，就有公式：f(4,x,y,z) = f(3,x,z,y),x->z,f(3,y,x,z).从而推出f(n,x,y,z) = f(n,x,z,y),x->z,f(n,y,x,z)!

综上所述：也就是说我们想移动n个盘子，就需要先移动n - 1个盘子；移动n - 1个盘子，就需要先移动n - 2个盘子 ………………；移动2个盘子，就必须先移动1个盘子；

（1）而移动1个盘子就是递归的终止条件

（2）而n个盘子变成n - 1个盘子就是递归的大问题变成小问题的方法

宏观角度分析递归：

再来回顾，宏观的细节

一：不要在意递归的细节展开图
二：把递归的函数当成一个“黑盒”
三：我们的无条件的相信“黑盒”可以为我们解决当前的子问题（再次强调，递归中的每个子问题的解题步骤都是一样）

具体构建一个递归算法：

（1）创建函数头 ——> 从重复子问题入手，将x柱子上的盘子，借助y柱子转移到z柱子上。从而有函数头为：dfs(int x,int y,int z,int n); x、y和z代表了柱子，n代表现在多少个盘子需要移动。x是开始柱，y是中转柱，z是目的柱。

（2）确定函数体 ——> 无条件相信他能帮我们解决每一个子问题的。

重复的子问题如下：

如从 x 号柱子将n - 1个盘子借助 z 号柱子移动到 y 号柱子上
将 x 号柱子将最后一个盘子移动到 z 号柱子上
将 y 号柱子上的n - 1个盘子移动到 z 号柱子上

从而有函数体为：

① dfs(x,z,y,n - 1); ② x.back -> z; ③ dfs(y,x,z,n - 1);

（3）递归出口：当剩下一个盘子的时候，也就是n == 1时。x.back -> z即可。

    //宏观角度分析递归
    //1.创建函数头
    //2.确定函数体，无条件相信他能帮我们解决每一个子问题的
    //3.递归出口
    public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
        dfs(A,B,C,A.size());
    }

    public void dfs(List<Integer> x,List<Integer> y,List<Integer> z,int size){
        //递归出口
        if(size == 1){
            z.add(x.remove(x.size() - 1));
            return;
        }

        //封装一个小黑盒
        //将x柱上的size - 1个盘子通过z柱子移动到y柱子上
        dfs(x,z,y,size - 1);
        //将a柱上的最后一个盘子移动到c柱子上
        z.add(x.remove(x.size() - 1));
        //将b柱上的size - 1个盘子通过a柱子移动到c柱子上
        dfs(y,x,z,size - 1);
    }

2. 合并两个有序链表

力扣题目链接

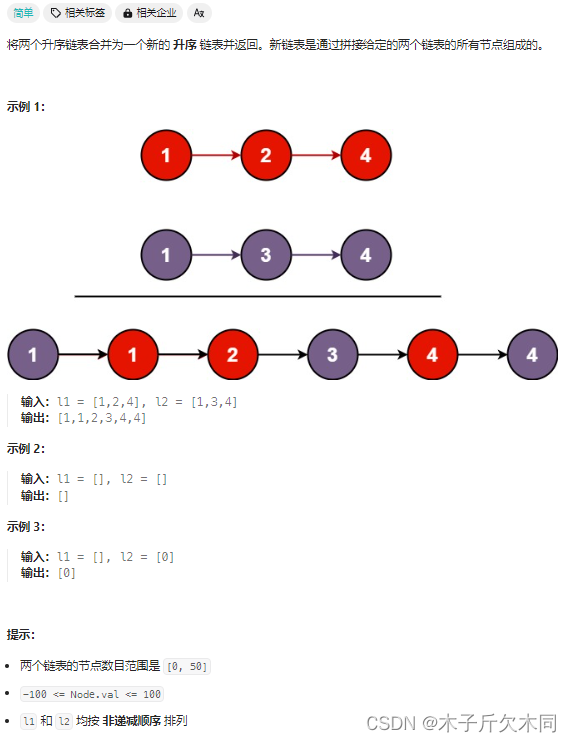
解析：
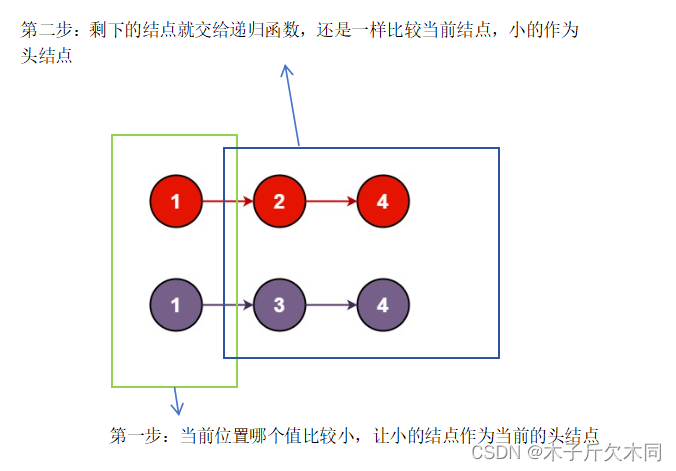
（1）递归函数的含义：交给你两个链表的头结点，你帮我把它们合并起来，并且返回合并后的头结点。
（2）函数体：选择两个头结点中较⼩的结点作为最终合并后的头结点，然后将剩下的链表交给递归函数去处理。
（3）递归出⼝：当某⼀个链表为空的时候，返回另外⼀个链表。

    // 法一：递归法
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        // 递归出口：当l1或者l2为空，就返回另一个不为空的链表
        if (l1 == null)
            return l2;
        if (l2 == null)
            return l1;
        //如果l1的值小于l2，那么就让l1作为头结点，剩下的结点继续比较
        if (l1.val <= l2.val) {
            l1.next = mergeTwoLists(l1.next,l2);
            return l1;
        }
        else{
            l2.next = mergeTwoLists(l1,l2.next);
            return l2;
        }
    }

3. 反转链表

力扣题目链接

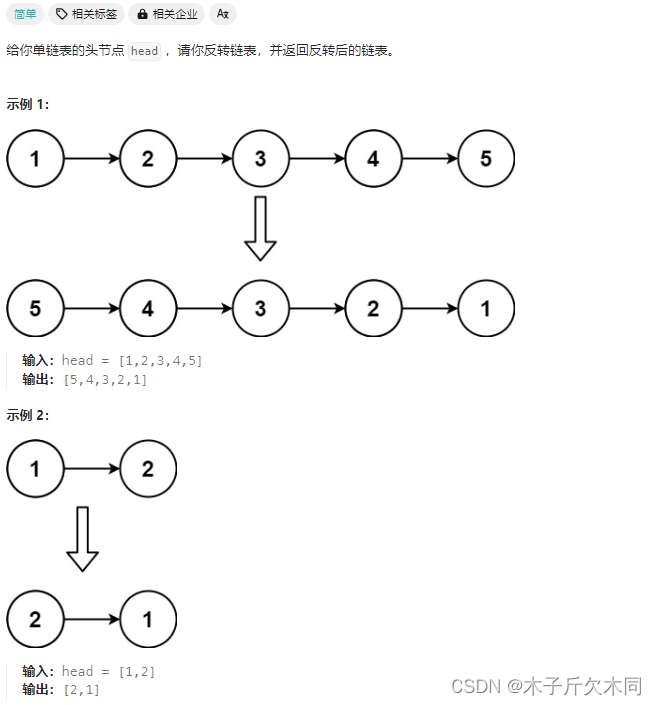
解析：

（1）递归函数的含义：交给你⼀个链表的头指针，你帮我逆序之后，返回逆序后的头结点。
（2）函数体：先把当前结点之后的链表逆序，逆序完之后，把当前结点添加到逆序后的链表后⾯即可。（相同的子问题）
（3）递归出⼝：当前结点为空或者当前只有⼀个结点的时候，不⽤逆序，直接返回。

    public ListNode reverseList(ListNode head) {
        return dfs(head);
    }
    public ListNode dfs(ListNode h){
        //递归出口：直接到找最后一个结点，类似后序遍历
        if(h == null || h.next == null){
            return h;
        }
        //找最后一个结点
        ListNode newNode = dfs(h.next);
        //从倒数第二个结点开始
        h.next.next = h;
        h.next = null;

        return newNode;
    }

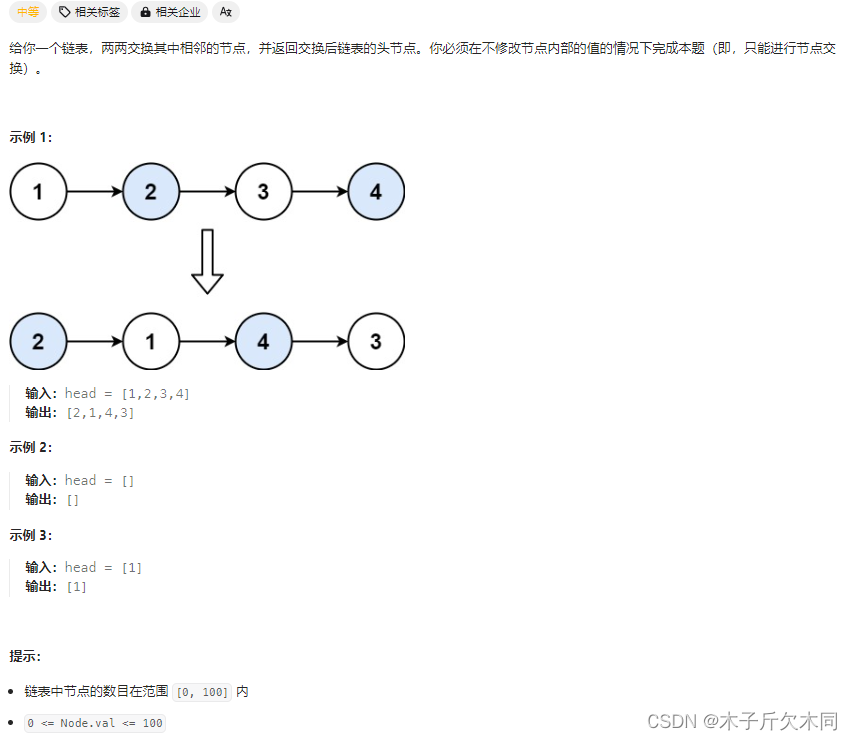
4. 两两交换链表中的结点

力扣题目链接

解析：

（1）递归函数的含义：交给你⼀个链表，将这个链表两两交换⼀下，然后返回交换后的头结点。
（2）函数体：先去处理⼀下第⼆个结点往后的链表，然后再把当前的两个结点交换⼀下，连接上后⾯处理后的链表。（相同的子问题）
（3）递归出⼝：当前结点为空或者当前只有⼀个结点的时候，不⽤交换，直接返回。

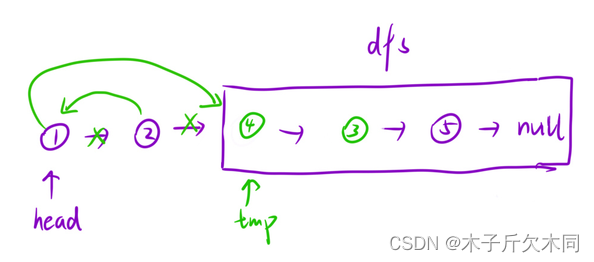
    //后序遍历
    public ListNode swapPairs(ListNode head) {
        //链表中节点的数目在范围 [0, 100] 内
        //如果只剩下一个结点就没必要交换了，因为是两两交换
        if(head == null || head.next == null){
            return head;
        }
        //先去交换在我之后之后的结点
        ListNode newNode = swapPairs(head.next.next);
        ListNode ret = head.next;
        head.next = newNode;
        ret.next = head;
        return ret;
    }

要先修改后面结点，再能修改当前结点，很类似后序遍历的方式。

5. 快速幂

力扣题目链接

解法一暴力循环

    public double myPow(double x, int n) {
        double ret = 1;
        int tmp = n;
        if(n < 0) n = -n;
        for(int i = 1;i <= n;i++){
            ret *= x;
        }
        if(tmp < 0) ret = 1.0 / ret;
        return ret;
    }

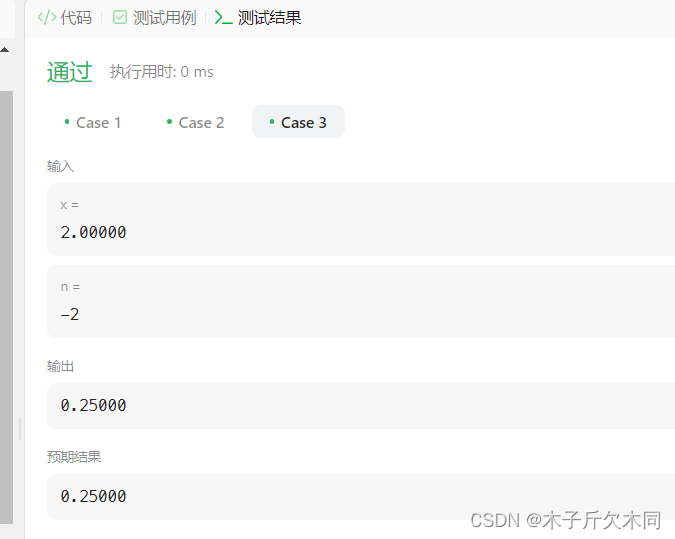
暴力循环可以解决较小的幂，当幂的值比较大就会报超时的错误！！！

所以有了如下两个改进方案：

解法二不断拆分

（1）递归函数的含义：求出 x 的 n 次⽅是多少，然后返回。
（2）函数体：先求出 x 的 n / 2 次⽅是多少，然后根据 n 的奇偶，得出 x 的 n 次⽅是多少。
（3）递归出⼝：当 n 为 0 的时候，返回 1 即可。

    //第二种方法：
    public double myPow(double x, int n) {
        return n < 0 ? 1.0 / pow(x,-n) : pow(x,n);
    }

    public double pow(double x,int n){
        if(n == 0)
            return 1.0;
        double tmp = pow(x,n/2);
        return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;
    }

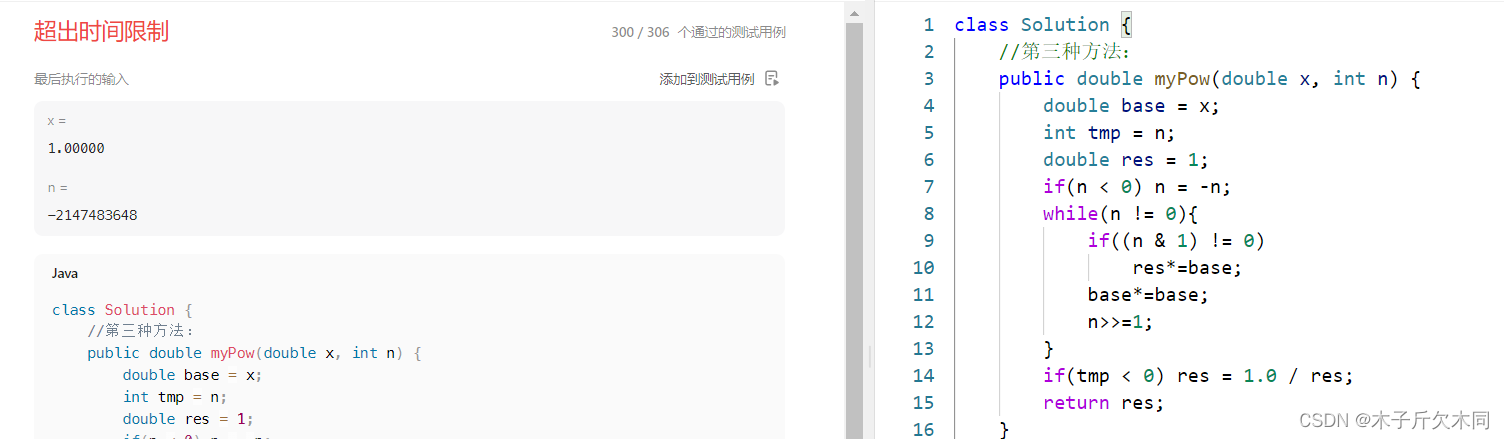
解法三利用了二进制的特点

例如算 $a^{11}$ :

分解： $a^{11}=a^{8+2+1} = a^{8}\times a^{2}\times a^{1}$

（1）而 $a^{8}$ 、 $a^{2}$ 、 $a^{1}$ 是倍乘关系，所以算 $a^{11}$ 不用11个a相乘，而是 $a^{2}=a^{1}\times a^{1}$ 得到， $a^{4} = a^{2} \times a^{2}$ ，而 $a^{8} = a^{4} \times a^{4}$ 得到。

（2）那么问题来了，如何将11分解成 11 = 8 + 2 + 1这样的倍乘关系呢？

答： $11_{10} = 1011_{2} = 2^{3}+2^{1}+2^{0} = 8+2+1$

（3）这里因为二进制的11中第三位为0，所以没有 $2^{2} = 4$ ，如果跳过4呢？1011中的0，就是需要跳过的 4。

（4） $11_{10} = 1011_{2} = 2^{3}+2^{1}+2^{0} = 8+2+1$

推算乘积：从低位往高位处理1011（右移一次，就把刚处理的低位移走了）

1011，处理末尾的1：计算a。 $res=a$ ；
1011，处理第2个1：计算 $a^{2}$ 。 $res = res\times a^{2} = a^{1+2}$ ；
1011，处理0：跳过 $a^{4}$ 。
1011，处理1：计算 $a^{8}$ 。 $res=res\times a^{8}=a^{1+2+8}$ 。

    //第三种方法：
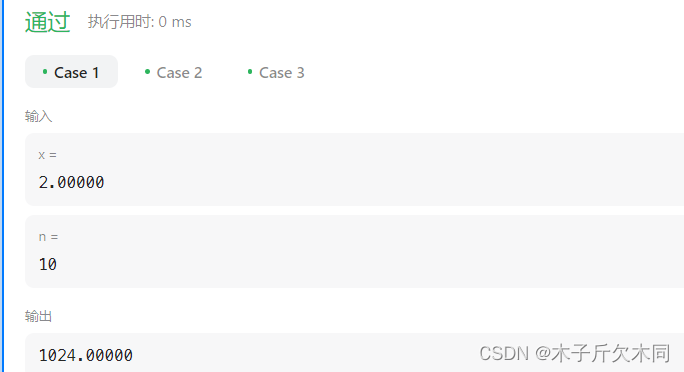
    public double myPow(double x, int n) {
        double base = x;
        int tmp = n;
        double res = 1;
        if(n < 0) n = -n;
        while(n != 0){
            if((n & 1) != 0) //如果n的最后一位是1，表示这个地方需要乘
                res*=base;
            base*=base;//推算乘积，在解析有说明
            n>>=1;//n右移一位，把刚处理过n的最后一位去掉
        }
        if(tmp < 0) res = 1.0 / res;
        return res;
    }