集成学习概念
集成学习是机器学习中的一种思想,它通过多个模型的组合形成一个精度更高的模型,参与组合的
模型成为弱学习器(弱学习器)。训练时,使用训练集依次训练出这些弱学习器,对未知的样本进
行预测时,使用这些弱学习器联合进行预测。
集成学习分类

Bagging
特点:
有放回的抽样(booststrap抽样)产生不同的训练集,从而训练不同的学习器
通过平权投票、多数表决的方式决定预测结果
弱学习器可以并行训练
Boosting
特点:
每一个训练器重点关注前一个训练器不足的地方进行训练
通过加权投票的方式,得出预测结果
串行的训练方式
代表模型
Bagging的代表模型:
1.随机森林算法
随机森林是基于 Bagging 思想实现的一种集成学习算法,采用决策树模型作为每一个弱学习器。
训练: 有放回的产生训练样本
随机挑选 n 个特征(n 小于总特征数量)
预测:平权投票,多数表决输出预测结果

随机森林API
from sklearn.ensemble import RandomForestClassifier # 分类
from sklearn.ensemble import RandomForestRegressor # 回归
n_estimators:决策树数量,(default =10)
Criterion:entropy、或者gini, (default= gini)
max_depth:指定树的最大深度,(default=None 表示树会尽可能的生长)
max features="auto”,决策树构建时使用的最大特征数量
bootstrap:是否采用有放回抽样,如果为False 将会使用全部训练样本,(defaut=True)
min_samples_split: 结点分裂所需最小样本数,(defaut=2)
# 如果节点样本数少于min_samples_split,则不会再进行划分
# 如果样本量不大,不需要设置这个值.
# 如果样本量数量级非常大,则推荐增大这个值.
min_samples_leaf:叶子节点的最小样本数,(default=1)
# 如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝
# 较小的叶子结点样本数量使模型更容易捕捉训练数据中的噪声.
min_impurity_split: 节点划分最小不纯度
# 如果某节点的不纯度(基尼系数,均方差)小于这个阈值,则该节点不再生成子节点,并变为叶子节点
# 一般不推荐改动默认值1e-7。2.Adaboost算法
Adaptive Boosting(自适应提升)基于 Boosting思想实现的一种集成学习算法核心思想是通过逐步提
高那些被前一步分类错误的样本的权重来训练一个强分类器。
构建过程
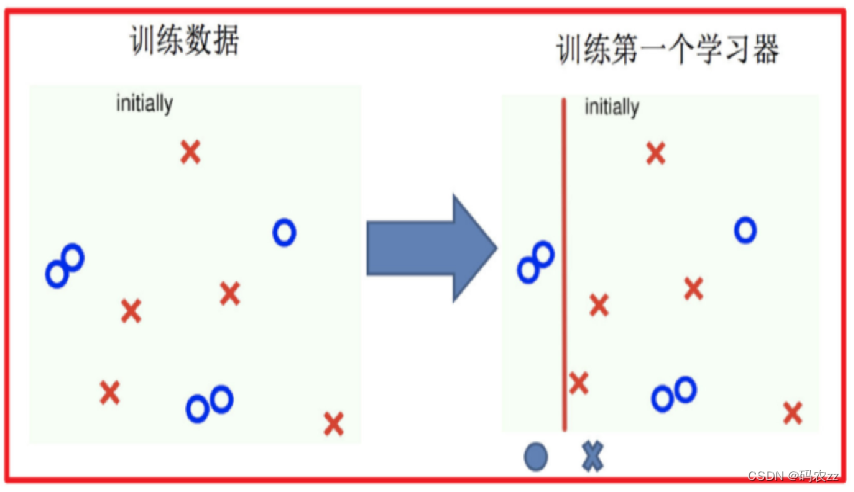
1 初始化数据权重,来训练第1个弱学习器。找最小的错误率计算模型权重,再更新模数据权重。
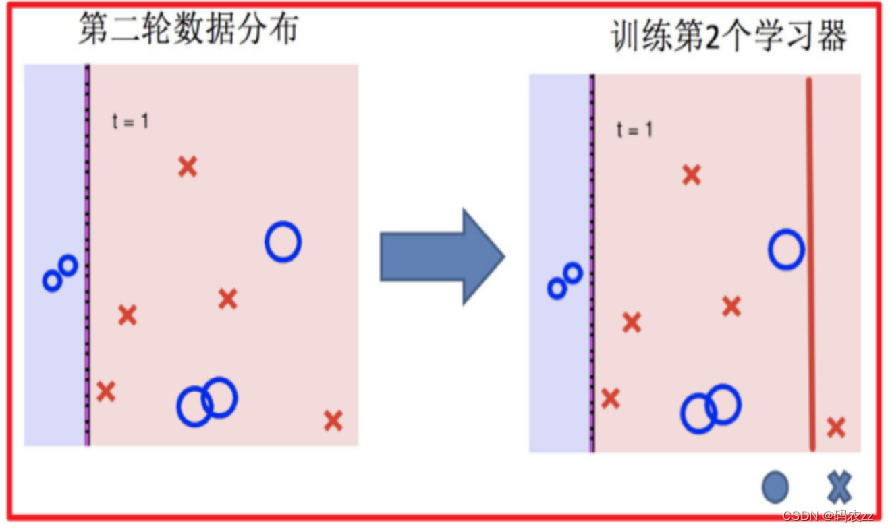
2 根据更新的数据集权重,来训练第2个弱学习器,再找最小的错误率计算模型权重,再更新模数
据权重。
3 依次重复第2步,训练n个弱学习器。组合起来进行预测。结果大于0为正类、结果小于0为负类
1.训练第一个学习器 2.调整数据分布

3.训练第二个学习器 4.再次调整数据分布
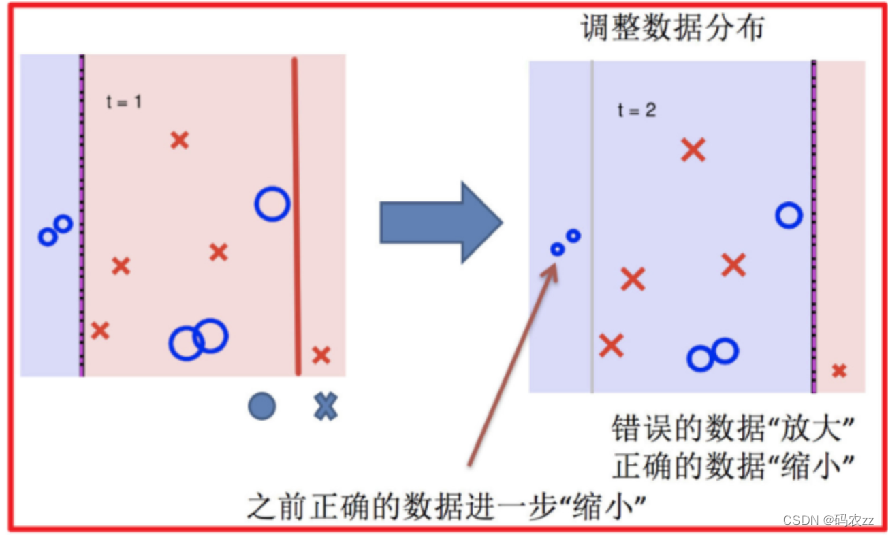
5.依次训练学习器,调整数据分布 6.整体过程实现
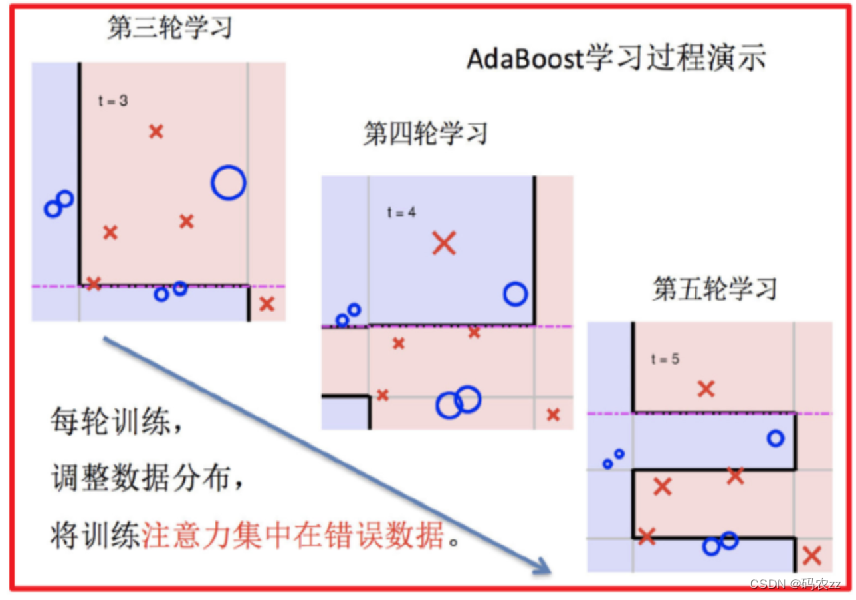
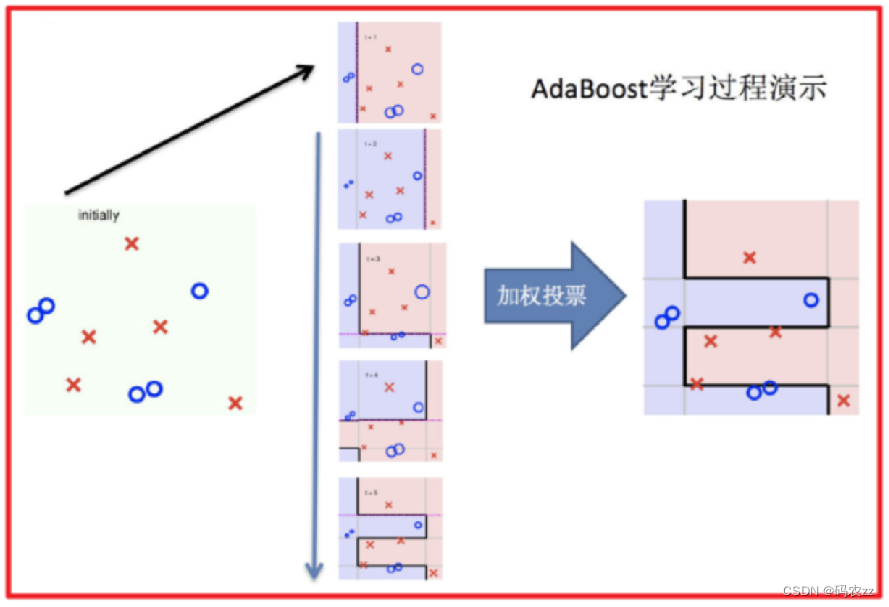
案例代码演示
# AdaBoost实战葡萄酒数据
import pandas as pd
from sklearn.model_selection import train_test_split # 划分
from sklearn.tree import DecisionTreeClassifier # 指定的决策树
from sklearn.ensemble import AdaBoostClassifier # 集成学习
from sklearn.metrics import accuracy_score # 评估
#%%
# 加载数据
df_wine = pd.read_csv('wine0501.csv')
df_wine = df_wine[df_wine['Class label']!=1] # 去掉一部分数据做二分类
x = df_wine[['Alcohol','Hue']]
y = df_wine['Class label']
#%%
X_train, X_test, y_train, y_test = train_test_split(x,y,random_state=22)
# 创建一个基学习器 决策树
dct_classifier = DecisionTreeClassifier(max_depth=1)
# 创建AdaBoost的分类器, 指定使用决策树分类器作为基学习器, 100棵树 学习率0.1
ada_classifier = AdaBoostClassifier(base_estimator=dct_classifier,n_estimators=100,learning_rate=0.1)
# 模型训练 评估
ada_classifier.fit(X_train,y_train)
print(ada_classifier.score(X_train, y_train))
print(ada_classifier.score(X_test, y_test))
3.梯度提升树
梯度提升树不再拟合残差,而是利用梯度下降的近似方法,利用损失函数的负梯度作为提升树算法
中的残差近似值。
假设:
前一轮迭代得到的强学习器是:fi-1(x)
损失函数为平方损失是:L(y,fi−1(x))
本轮迭代的目标是找到一个弱学习器:hi(x)即 fi(X)=fi_1(X)+hi(X)
让本轮的损失最小化: L(y, fi(x))=L(y, fi−1(x) + hi(x)) 损失函数定义为平方损失L(y, f(x))=1/2(y-
f(X))2 得到L(y, fi(x)) = 1/2(y-(fi-1(X)+hi(X)))²
则要拟合的负梯度为:
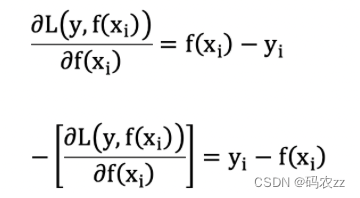
GBDT 拟合的负梯度就是残差。如果我们的 GBDT 进行的是分类问题,则损失函数变为 logloss,
此时拟合的目标值就是该损失函数的负梯度值
构建流程
1 初始化弱学习器(目标值的均值作为预测值)
2 迭代构建学习器,每一个学习器拟合上一个学习器的负梯度
3 直到达到指定的学习器个数
4 当输入未知样本时,将所有弱学习器的输出结果组合起来作为强学习器的输出
案例代码演示
# 导入库
import pandas as pd
from sklearn.model_selection import train_test_split # 划分
from sklearn.ensemble import GradientBoostingClassifier # 梯度提升树
from sklearn.metrics import classification_report # 分析性能
from sklearn.model_selection import GridSearchCV # 交叉网格
from sklearn.metrics import accuracy_score # 评估
# 读取数据
titanic_df = pd.read_csv('titanic/train.csv')
titanic_df
#%%
# 确定x,y
x = titanic_df[['Pclass','Age','Sex']]
y = titanic_df['Survived']
#%%
# 缺失值处理
x['Age'].fillna(x['Age'].mean(), inplace=True)
#%%
# 年龄进行缺失值填充
x['Age'].fillna(x['Age'].mean(),inplace = True)
#%%
# 性别编码
X = pd.get_dummies(x)
#%%
# 划分
X_train, X_test, y_train, y_test = train_test_split(X,y,stratify=y,random_state=66)
# GBDT 梯度提升树 交叉网格
rf_classifier = GradientBoostingClassifier()
# 参数解释: n_estimators弱学习器的数量 max_depth树的最大深度 learning_rate 学习率
parmas = {"n_estimators": [ 50,100,150], "max_depth": [2,3,5, 8, 10], "learning_rate":[0.1,0.3,0.5,0.7,0.9]}
# 交叉网格
gs_estimator = GridSearchCV(rf_classifier,param_grid=parmas,cv=4)
gs_estimator.fit(X_train,y_train)
x_pre = gs_estimator.predict(X_test)
#%%
gs_estimator.best_params_ # 最佳参数组合
#%%
gs_estimator.best_score_ # 最佳分数
#%%
gs_estimator.score(X_test, y_test)
#%%
# 分析性能
print(classification_report(x_pre,y_test, target_names=['丧生', '生还']))
4.XGBoost
极端梯度提升树,集成学习方法的王牌,在数据挖掘比赛中,大部分获胜者用了XGBoost。
XGBoost 基本的原理还是 GBDT, 是对GBDT的优化
xgb 在GBDT的基础上 给损失函数引入了正则
![]()
![]()
γT 中的 T 表示一棵树的叶子结点数量。
λ||w||^2中的 w 表示叶子结点输出值组成的向量, ||w||^ 向量的模;
λ对该项的调节系数可以避免过拟合
案例代码演示
import pandas as pd
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
#%%
# 获取数据
data = pd.read_csv('红酒品质分类.csv')
x = data.iloc[:,:-1] # 特征数据
y = data.iloc[:,-1] -3
#%%
# 划分
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.2,stratify=y,random_state=22)
# objective 当前解决的问题使用的目标函数 multi:多分类:softmax 目标函数
# eval_metric 评估指标 merror 多分类的错误率
# n_estimators 基学习器的数量
# # eta 学习率
estimator = xgb.XGBClassifier(n_estimators = 100,eval_metric='merror',eta=0.1,objective='multi:softmax')
estimator.fit(x_train,y_train)
y_pred = estimator.predict(x_test)
print(classification_report(y_test,y_pred))
#%%
# 计算权重
from sklearn.utils import class_weight
class_weights = class_weight.compute_sample_weight(class_weight='balanced',y=y_train)
#%%
# 增加权重 在训练评估一下
estimator.fit(x_train,y_train,sample_weight=class_weights)
y_pred = estimator.predict(x_test)
print(classification_report(y_test,y_pred))
#%%
# 对xgb调参
from sklearn.model_selection import GridSearchCV,StratifiedKFold
# 数据切成5份,保证每一份y的比例 shuffle 乱序
spliter =StratifiedKFold(n_splits=5,shuffle=True)
params = {'n_estimators':[50,100,150],'eta':[0.1,0.3,0.5,0.9],'max_depth':[1,3,5]}
estimator = xgb.XGBClassifier(n_estimators = 100,eval_metric='merror',eta=0.1,objective='multi:softmax')
# 交叉验证
gs_estimator = GridSearchCV(estimator=estimator,param_grid=params,cv=spliter)
gs_estimator.fit(x_train,y_train)
# 当样本分布不均衡的时候,做交又验证和网格搜索,使用StratifiedKFold, GridsearchCV 中v参数 直接传入StratifiedKFold的
# 对象,不要直接传入一个数字,这样能保证训练集,验证集,每个类别的数据都有,并按比例划分
#%%
gs_estimator.best_score_
#%%
gs_estimator.best_params_
#%%
import joblib
# 模型的保存
joblib.dump(estimator,'xgboost_wine.pth')
#%%
# 模型的加载
estimator = joblib.load('xgboost_wine.pth')
estimator.predict(x_test)