算法就要多练,我在国庆节放假的时间编写了图的算法题,写完让我受益匪浅,希望可以帮助到大家.

前言

一、图的数据结构

1.图的邻接表数据结构定义

2.图的邻接矩阵的存储形式

二、邻接表建立图代码

三、邻接表删除边(基本操作考试不考)

四、邻接表删除顶点及销毁整个图结构(基本操作考试不考)

五、获取第一个邻接顶点

六、获取下一个邻接顶点

七、使用二维数组建立图

八、将邻接表存储的有向图G转换成逆邻接表存储

九、设计算法计算有向图的所有顶点的度

十、将邻接表表示的有向网转换成邻接矩阵(有向网带权值默认权值都为1)

十一、图的广度优先遍历(BFS)(这是解决图基本问题的基本算法,一定要理解并应用)

 十二、图的深度优先遍历(DFS)(这是解决图基本问题的基本算法,一定要理解并应用)

十三、判断以邻接表为存储结构的有向图G是否存在环

 十四、设计算法求出以邻接表存储的有向图中所有从顶点v到w的简单路径

 十五、设计算法求解以邻接表存储de有向图G中所有从顶点v到顶点w长度为d的路径

 十六、设计算法对有向无环图进行拓扑排序(AOV网)

 十七、创建以邻接矩阵为存储结构的有向图

 十八、编写迪杰斯特拉算法

最终总代码和测试

总结

---

---

前言

图的算法题多种多样,但都是最基本的算法而来,只要深入理解图的数据结构与基本的算法,任何问题只要稍加思考就可以解决,编写这篇文章不知不觉想起当时在宿舍敲代码的自己,大一的时候我学习了数据结构,当时考的分刚及格,我时常抱怨过去的自己,为什么当时一无所知,但有一天我忽然理解,虽然会有一些懊悔,但现在的时间节点与我过去的自己相比是提升的,这才是过去到现在的真正意义,这800行代码希望可以帮助到大家.

---

一、图的数据结构

1.图的邻接表数据结构定义

//定义表结点的数据类型
typedef struct ArcNode {
	int adjVex;//终端节点
	struct ArcNode* nextArc;
	int weight;
}ArcNode;
//定义头节点的数据类型
typedef char VertexType;
typedef struct VNode {
	VertexType data;//顶点数据
	ArcNode* firstArc;//指向第一个表结点
	//AdjList是一个包含所有头结点的数组
}VNode,AdjList[MAX_VERTEX_NUM];

//定义图的临接表类型
typedef struct {
	AdjList vertices;
	int Vexnum;//总节点数
	int Arcnum;//总边数
	int Kind;//图的类型
	int MaxVexnum;
}ALGraph;//临界表类型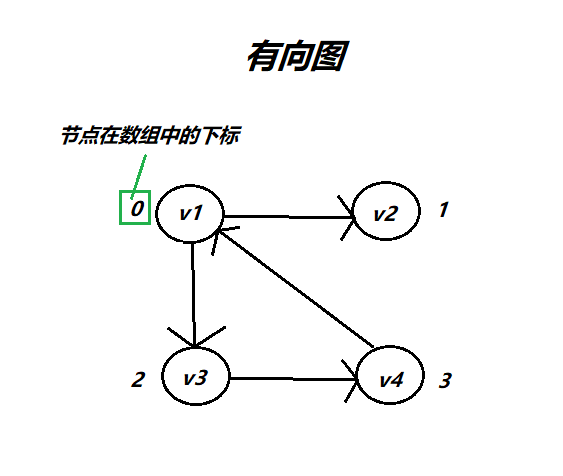

图的数据结构这部分知识大家看王道的就可以啦,大家多写几遍,就熟悉了,图的数据结构是最基本的,在后续代码中都会用到图的邻接表的存储形式.

2.图的邻接矩阵的存储形式

//定义图的邻接矩阵存储结构
typedef  struct MGraph {
	VertexType verList[MAX_VERTEX_NUM];
	int arcMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
	int Vexnum;
	int Arcnum;
	int Kind;
}MGraph;

图的数据结构的选择可以按照现实所需来自行选择.

二、邻接表建立图代码

说了这么多我们就开始敲代码吧.

//定义初始化图函数
void InitALGraph(ALGraph &G,int kind) {//kind表示是有向图还是无向图
	//由于我们定义了临接表的数据类型所以初始化比较简单
	for (int i = 0; i < MAX_VERTEX_NUM; i++) {
		G.vertices[i].firstArc = NULL;//这里只初始化了表节点的指针,数据暂时不用管
	}
	G.Vexnum = 0;
	G.Kind = kind;
	G.MaxVexnum = MAX_VERTEX_NUM;
	G.Arcnum = 0;
}
//定义插入表节点函数
void InsertVertex(ALGraph &G,VertexType v) {
	if (G.Vexnum >= G.MaxVexnum) {
		return;
	}
	G.vertices[G.Vexnum++].data = v;
}
//打印邻接表
void printALGraph(ALGraph G) {
	for (int i = 0; i < G.Vexnum; i++) {//遍历整个邻接表
		printf("%d %c -> ", i , G.vertices[i].data);
		ArcNode* p = G.vertices[i].firstArc;
		while (p != NULL) {
			printf("%d %c -> ",p->adjVex, G.vertices[p->adjVex].data);
			p = p->nextArc;
		}
		printf("NULL");
		printf("\n");
	}
	printf("图中有%d个节点,%d条边.\n", G.Vexnum, G.Arcnum);
}

//获取顶点的位置函数
int getVertexpos(ALGraph G, VertexType v) {
	for (int i = 0; i < G.Vexnum; i++) {//遍历表节点数组
		if (G.vertices[i].data == v) {
			return i;
		}
	}
	return -1;//顶点在表里不存在
}
//定义插入节点函数
void InsertArc(ALGraph& G, VertexType v1, VertexType v2) {
	int posv1 = getVertexpos(G, v1);//获取节点位置
	int posv2 = getVertexpos(G, v2);
	if (posv1 == -1 || posv2 == -1) {//判读两个节点是否都在图里
		printf("插入边的节点不存在,插入失败!!!!!!!\n");
		return;
	}
	else {
		//插入边前还需判断该是否存在该条边,这里就不在判断了,考试也不用写
		ArcNode* tmp = NULL;
		tmp = (ArcNode*)malloc(sizeof(ArcNode));
		assert(tmp);
		tmp->adjVex = posv2;//采用头插法插入节点
		tmp->nextArc = G.vertices[posv1].firstArc;
		G.vertices[posv1].firstArc = tmp;

		if (G.Kind == 0) {//无向图
			ArcNode* tmp = NULL;
			tmp = (ArcNode*)malloc(sizeof(ArcNode));
			assert(tmp);
			tmp->weight = 1;
			tmp->adjVex = posv1;
			tmp->nextArc = G.vertices[posv2].firstArc;
			G.vertices[posv2].firstArc = tmp;
		}
		G.Arcnum++;
	}
}

//定义创建测试图的函数
void creat(ALGraph &G) {
	InitALGraph(G, 0);//这里初始化无向图
	InsertVertex(G, 'A');//插入节点ABCDE
	InsertVertex(G, 'B');
	InsertVertex(G, 'C');
	InsertVertex(G, 'D');
	InsertVertex(G, 'E');
	InsertArc(G, 'A', 'B');//插入边
	InsertArc(G, 'A', 'D');
	InsertArc(G, 'B', 'C');
	InsertArc(G, 'B', 'E');
	InsertArc(G, 'C', 'D');
	InsertArc(G, 'C', 'E');
}

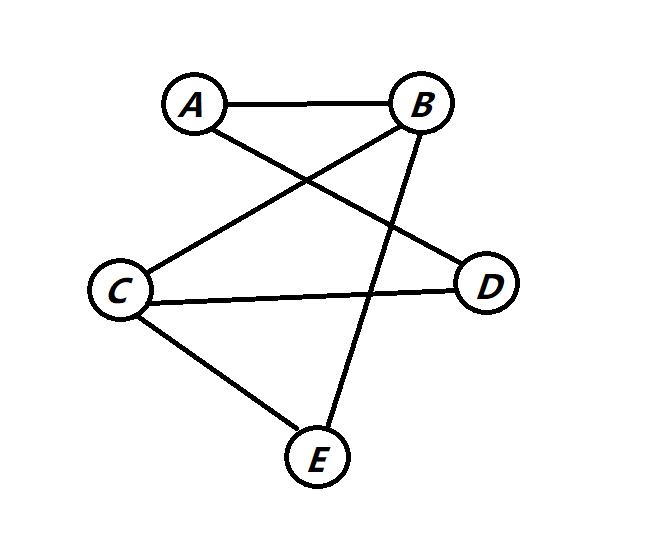
为了方便大家观看我将对应的节点也打印出来更加清晰.

三、邻接表删除边(基本操作考试不考)

这些基本操作在实际上可以用到,思想也很简单,就是链表的删除.

//定义删除边函数
void RemoveArc(ALGraph& G, VertexType v1, VertexType v2) {
	int posv1 = getVertexpos(G, v1);
	int posv2 = getVertexpos(G, v2);
	if (posv1 == -1 || posv2 == -1) {
		printf("删除边的节点不存在,插入失败!!!!!!!\n");
		return;
	}
	//链表节点删除一样
	ArcNode* pNode = G.vertices[posv1].firstArc;
	ArcNode* preNode = NULL;
	while (pNode != NULL && pNode->adjVex != posv2) {
		preNode = pNode;
		pNode = pNode->nextArc;
	}
	if (pNode != NULL) {//找到了该边
		if (preNode == NULL) {//该节点是第一个节点需要修改firstArc,或者直接判断pNode == G.vertices[posv1].firstArc;
			G.vertices[posv1].firstArc = pNode->nextArc;
		}
		else {//不是第一个节点
			preNode->nextArc = pNode->nextArc;
		}
		free(pNode);
		pNode = NULL;
	}
	else {
		printf("图中没有该边删除失败!!!!!!!!\n");
		return;
	}
	if (G.Kind == 0) {//由于在电脑上故可以在删除函数里判断,在手写时,可以在外面判断图的类型之后调用两次函数
		ArcNode* pNode = G.vertices[posv2].firstArc;
		ArcNode* preNode = NULL;
		while (pNode != NULL && pNode->adjVex != posv1) {
			preNode = pNode;
			pNode = pNode->nextArc;
		}
		if (pNode != NULL) {
			if (preNode == NULL) {
				G.vertices[posv2].firstArc = pNode->nextArc;
			}
			else {
				preNode->nextArc = pNode->nextArc;
			}
			free(pNode);
			pNode = NULL;
		}
		else {
			printf("图中没有该边删除失败!!!!!!!!\n");
			return;
		}
	}
	G.Arcnum--;
	printf("删除%c -> %c成功!\n", v1, v2);
	if (G.Kind == 0) {
		printf("删除%c -> %c成功!\n", v2, v1);
	}
}

其实我感觉我这段代码有冗余的地方,为了方便大家理解我就没有修改,主要的是代码思想,理解万岁.

四、邻接表删除顶点及销毁整个图结构(基本操作考试不考)

//定义删除节点函数
//算法思想:将所有的关于删除节点的边,之后该节点保存邻接表左后一个节点的信息,然后将所有与最后一个节点有关的边的指向信息改为删除节点的位置
void RemoveVextex(ALGraph& G, VertexType vertex) {
	int posv = getVertexpos(G, vertex);
	if (posv == -1) {
		return;
	}
	//删除与vertex节点有关的所有边
	VertexType v;
	ArcNode* p = G.vertices[posv].firstArc;
	while (p != NULL) {
		v = G.vertices[p->adjVex].data;
		p = p->nextArc;
		RemoveArc(G, vertex, v);//删除边函数
	}
	//将最后的节点信息复制到删除节点的位置
	G.vertices[posv].firstArc = G.vertices[G.Vexnum - 1].firstArc;
	G.vertices[G.Vexnum - 1].firstArc = NULL;
	G.vertices[posv].data = G.vertices[G.Vexnum - 1].data;
	G.Vexnum--;
	//将所有有关最后一个节点的边,修改其指向位置为删除节点的位置
	ArcNode* s = NULL;
	p = G.vertices[posv].firstArc;
	while (p != NULL) {//遍历最后一个节点的边信息
		s = G.vertices[p->adjVex].firstArc;
		while (s != NULL && s->adjVex != G.Vexnum) {
			s = s->nextArc;
		}
		if (s != NULL) {
			s->adjVex = posv;//修改指向
		}
		p = p->nextArc;
	}
}
//定义销毁图函数
void DestroyGraph(ALGraph& G) {
	for (int i = G.Vexnum-1; i>=0; i--) {//从尾部删除因为是往前复制的
		RemoveVextex(G, G.vertices[i].data);
	}
	printf("销毁图成功!\n");
}

五、获取第一个邻接顶点

//定义获取第一个邻接顶点
int GetFirstNeighbor(ALGraph G, VertexType v) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return -1;//没有该节点
	}
	ArcNode* p = G.vertices[posv].firstArc;
	if (p != NULL) {//第一个节点为空
		return p->adjVex;
	}
	return -1;
}

 六、获取下一个邻接顶点

//定义获取下一个邻接顶点
int GetNextNeighbor(ALGraph G, VertexType v1, VertexType v2) {//获取v1顶点v2后的下一个顶点
	int posv1 = getVertexpos(G, v1);
	int posv2 = getVertexpos(G, v2);
	if (posv1 == -1 || posv2 == -1) {
		return -1;
	}
	//找到v1到v2的边节点
	ArcNode* p = G.vertices[posv1].firstArc;
	while (p != NULL && p->adjVex != posv2) {
		p = p->nextArc;
	}
	//找到了且下一个节点不为空
	if (p != NULL && p->nextArc!=NULL) {
		return p->nextArc->adjVex;
	}
	return -1;
}

七、使用二维数组建立图

//使用二维数组建立图
void creatALGraphArr(ALGraph& G, VertexType verList[], int vernum, char arcList[][2], int arcnum,int kind) {
	//基本信息一定要先初始化因为后面函数要用到基本信息
	G.Kind = kind;//建立该图的类型
	G.Vexnum = vernum;
	G.Arcnum = arcnum;
	G.MaxVexnum = MAX_VERTEX_NUM;
	//初始化表节点
	for (int i = 0; i < vernum; i++) {
		G.vertices[i].data = verList[i];//节点数据
		G.vertices[i].firstArc = NULL;//节点第一个指向的边节点为NULL
	}
	//插入边节点
	for (int i = 0; i < arcnum; i++) {
		VertexType v1 = arcList[i][0];
		VertexType v2 = arcList[i][1];
		int posv1 = getVertexpos(G, v1);
		int posv2 = getVertexpos(G, v2);
		if (posv1 == -1 || posv2 == -1) {
			printf("边的节点不在邻接表!失败!!!!!\n");
			break;
		}
		ArcNode* pNode = (ArcNode*)malloc(sizeof(ArcNode));
		assert(pNode);
		pNode->weight = 1;
		pNode->adjVex = posv2;
		//头插法
		pNode->nextArc = G.vertices[posv1].firstArc;
		G.vertices[posv1].firstArc = pNode;
		//无向图两个节点都要插入
		if (G.Kind == 0) {
			ArcNode* pNode = (ArcNode*)malloc(sizeof(ArcNode));
			assert(pNode);
			pNode->adjVex = posv1;
			//头插法
			pNode->nextArc = G.vertices[posv2].firstArc;
			G.vertices[posv2].firstArc = pNode;
		}
	}
}

八、将邻接表存储的有向图G转换成逆邻接表存储

//将邻接表存储的有向图G转换成逆邻接表存储
void reverseALGraph(ALGraph G, ALGraph& rG) {
	rG.MaxVexnum = MAX_VERTEX_NUM;
	rG.Arcnum = 0;
	rG.Kind = G.Kind;
	rG.Vexnum = G.Vexnum;
	//复制表节点
	for (int i = 0; i < G.Vexnum; i++) {
		rG.vertices[i].data = G.vertices[i].data;
		rG.vertices[i].firstArc = NULL;//头节点指针域制空
	}
	for (int i = 0; i < G.Vexnum; i++) {
		VertexType v1 = G.vertices[i].data;
		ArcNode* p = G.vertices[i].firstArc;
		while (p != NULL) {
			VertexType v2 = G.vertices[p->adjVex].data;
			InsertArc(rG, v2, v1);
			p = p->nextArc;
		}
	}
}

九、设计算法计算有向图的所有顶点的度

//设计算法计算有向图的所有顶点的度
//算法思想:有向图的度只需遍历所有边遇到一个边弧头和弧尾的入度加一
void GetDegreedVertex(ALGraph G,int degree[]) {
	for (int i = 0; i < G.Vexnum; i++) {
		ArcNode* pNode = G.vertices[i].firstArc;
		while (pNode != NULL) {
			degree[i]++;
			degree[pNode->adjVex]++;
			pNode = pNode->nextArc;
		}
	}
}

十、将邻接表表示的有向网转换成邻接矩阵(有向网带权值默认权值都为1)

//将邻接表表示的有向网转换成邻接矩阵(有向网带权值默认权值都为1)
#define INF 999999
void convertAdjList(ALGraph G, MGraph& mG) {
	mG.Arcnum = G.Arcnum;
	mG.Vexnum = G.Vexnum;
	mG.Kind = G.Kind;
	//初始化邻接矩阵
	for (int i = 0; i < G.Vexnum; i++) {
		for (int j = 0; j < G.Vexnum; j++) {
			mG.arcMatrix[i][j] = INF;
		}
	}
	//遍历邻接表转换成邻接矩阵
	for (int i = 0; i < G.Vexnum; i++) {
		mG.verList[i] = G.vertices[i].data;
		ArcNode* pNode = G.vertices[i].firstArc;
		while (pNode != NULL) {
			int posv1 = i;
			int posv2 = pNode->adjVex;
			mG.arcMatrix[posv1][posv2] = pNode->weight;
			pNode = pNode->nextArc;
		}
	}
}
//定义打印邻接矩阵函数
void printMGraph(MGraph mG) {
	printf(" ");
	for (int i = 0; i < mG.Vexnum; i++) {
		printf("%10.c ", mG.verList[i]);
	}
	printf("\n");
	for (int i = 0; i < mG.Vexnum; i++) {
		printf("%c ", mG.verList[i]);
		for (int j = 0; j < mG.Vexnum; j++) {
			printf("%10.d ", mG.arcMatrix[i][j]);
		}
		printf("\n");
	}
	printf("该邻接矩阵有%d个节点,%d条边\n", mG.Vexnum, mG.Arcnum);
}

十一、图的广度优先遍历(BFS)(这是解决图基本问题的基本算法,一定要理解并应用)

//图的广度优先遍历(BFS)(这是解决图基本问题的基本算法,一定要理解并应用)
//算法思想:图的广度优先遍历类似与树的层序遍历,借助队列辅助完成,要借助visited数组
void BFS(ALGraph G,VertexType v,int visited[]){
	int posv = getVertexpos(G, v);
	if (posv == -1) {//顶点 不在邻接表里
		return;
	}
	printf("%c ", v);
	visited[posv] = 1;
	//定义辅助数组队列
	int Queue[40] = { 0 };//注意这里只申请了40空间
	int front = 0;
	int rear = 0;
	Queue[++rear] = posv;
	while (front != rear) {
		int postmp = Queue[++front];
		ArcNode* pNode = NULL;
		for (pNode = G.vertices[postmp].firstArc; pNode != NULL; pNode = pNode->nextArc) {
			int adj = pNode->adjVex;
			if (visited[adj] == 0) {//邻接的顶点没有访问.进队
				printf("%c ", G.vertices[adj].data);
				visited[adj] = 1;
				Queue[++rear] = adj;
			}
		}
	}
}

void BFSTraverse(ALGraph G) {
	int visited[MAX_VERTEX_NUM];
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	for (int i = 0; i < G.Vexnum; i++) {
		if (visited[i] == 0) {
			BFS(G, G.vertices[i].data, visited);
		}
	}
	printf("\n");
}

 十二、图的深度优先遍历(DFS)(这是解决图基本问题的基本算法,一定要理解并应用)

//图的深度优先遍历(DFS)(这是解决图基本问题的基本算法,一定要理解并应用)
//算法思想:图的深度优先遍历类于树的三种遍历方式,应用递归,要借助visited数组
void DFS(ALGraph G, VertexType v, int visited[]) {
	int posv = getVertexpos(G, v);
	printf("%c ", v);
	visited[posv] = 1;
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			DFS(G, G.vertices[adj].data, visited);
		}
		pNode = pNode->nextArc;
	}
}

void DFSTraverse(ALGraph G) {
	int visited[MAX_VERTEX_NUM];
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	for (int i = 0; i < G.Vexnum; i++) {
		if (visited[i] == 0) {
			DFS(G, G.vertices[i].data, visited);
		}
	}
	printf("\n");
}

十三、判断以邻接表为存储结构的有向图G是否存在环

//判断以邻接表为存储结构的有向图G是否存在环
//算法思想:以深度优先遍历为思想,设置顶点访问状态为0:未访问,1:正在访问,2:访问完成,如果访问的过程中访问到正在访问的顶点则说明有环
int DFSTraversing(ALGraph G, VertexType v,int visited[]) {
	int ret = 0;
	int posv = getVertexpos(G, v);
	visited[posv] = 1;
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			ret = DFSTraversing(G, G.vertices[adj].data, visited);
		}
		else if (visited[adj] == 1) {
			return 1;
		}
		if (ret == 1) {
			return 1;
		}
		pNode = pNode->nextArc;
	}
	visited[posv] = 2;
	return 0;
}

void isExistRing(ALGraph G) {
	int visited[MAX_VERTEX_NUM];
	int ret = 0;
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	for (int i = 0; i < G.Vexnum; i++) {
		if (visited[i] == 0) {
			ret = DFSTraversing(G, G.vertices[i].data, visited);
			if (ret == 1) {
				printf("%d has ring!\n",ret);
				break;
			}
		}
	}
	if (ret == 0) {
		printf("hasn't ring !\n");
	}
}

 十四、设计算法求出以邻接表存储的有向图中所有从顶点v到w的简单路径

//设计算法求出以邻接表存储的有向图中所有从顶点v到w的简单路径
//算法思想:还是以深度优先遍历为思想,与判断存在路径有异曲同工之妙
void printVertexList(VertexType verlist[], int verlength) {
	for (int i = 0; i < verlength; i++) {
		printf("%c ", verlist[i]);
	}
	printf("\n");

}
void DFSTraversing3(ALGraph G,VertexType v,VertexType w,int visited[],VertexType verList[],int &verlength) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return;
	}
	visited[posv] = 1;
	verList[verlength++] = v;
	if (v == w) {//找到目标节点打印路径
		printVertexList(verList, verlength);
	}
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			DFSTraversing3(G, G.vertices[adj].data, w, visited, verList, verlength);
		}
		pNode = pNode->nextArc;
	}
	visited[posv] = 0;//退出访问寻找其他路径
	verlength--;
}

void getPath(ALGraph G,VertexType src,VertexType dest) {
	int visited[MAX_VERTEX_NUM];
	VertexType verlist[MAX_VERTEX_NUM];
	int verlength = 0;
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	printf("%c 到 %c 的路径有\n",src,dest);
	DFSTraversing3(G, src, dest, visited, verlist, verlength);
}

 十五、设计算法求解以邻接表存储de有向图G中所有从顶点v到顶点w长度为d的路径

//设计算法求解以邻接表存储de有向图G中所有从顶点v到顶点w长度为d的路径
//算法思想:还是以深度优先遍历的思想,与上面的算法异曲同工之妙
void DFSTraversing4(ALGraph G, VertexType v, VertexType w, int visited[], VertexType verList[], int& verlength, int distant) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return;
	}
	verList[verlength++] = v;
	visited[posv] = 1;
	if (v == w && distant == 0) {
		printVertexList(verList, verlength);
	}
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			DFSTraversing4(G, G.vertices[adj].data, w, visited, verList, verlength, distant-1);
		}
		pNode = pNode->nextArc;
	}
	visited[posv] = 0;
	verlength--;
}
void getPathdistant(ALGraph G, VertexType src, VertexType dest,int distant) {
	int visited[MAX_VERTEX_NUM];
	VertexType verlist[MAX_VERTEX_NUM];
	int verlength = 0;
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	printf("%c 到 %c 的路径长度为%d的路径有\n", src, dest,distant);
	DFSTraversing4(G, src, dest, visited, verlist, verlength,distant);
}

 十六、设计算法对有向无环图进行拓扑排序(AOV网)

//设计算法对有向无环图进行拓扑排序(AOV网)
//算法思想:对图进行深度优先遍历为逆拓扑排序
void DFSTraversing5(ALGraph G,VertexType v,int visited[] ,VertexType verlist[],int &verlength) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return;
	}
	visited[posv] = 1;
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			DFSTraversing5(G, G.vertices[adj].data, visited, verlist, verlength);
		}
		pNode = pNode->nextArc;
	}
	verlist[verlength++] = v;
}

void printlogicsort(VertexType verlist[],int verlength) {
	printf("拓扑排序的序列为:");
	for (int i = verlength - 1; i >= 0; i--) {
		printf("%c ", verlist[i]);
	}
	printf("\n");
}
void getlogicsort(ALGraph G) {
	int visited[MAX_VERTEX_NUM];
	VertexType verlist[MAX_VERTEX_NUM];
	int verlength = 0;
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	for (int i = 0; i < G.Vexnum; i++) {
		if (visited[i] == 0) {
			DFSTraversing5(G, G.vertices[i].data, visited, verlist, verlength);
		}
	}
	printlogicsort(verlist, verlength);
}

 十七、创建以邻接矩阵为存储结构的有向图

//创建以邻接矩阵为存储结构的有向图
typedef struct arc {
	int pos1;
	int pos2;
	int weight;
}arc,ArcList[MAX_VERTEX_NUM];

void creatMGraph(MGraph &mG,VertexType verlist[],int verlength,ArcList arclist,int arclength) {
	mG.Vexnum = verlength;
	mG.Arcnum = arclength;
	mG.Kind = 1;
	for (int i = 0; i < verlength; i++) {
		mG.verList[i] = verlist[i];
	}
	for (int i = 0; i < mG.Vexnum; i++) {
		for (int j = 0; j < mG.Vexnum; j++) {
			mG.arcMatrix[i][j] = INF;
		}
	}
	for (int i = 0; i < arclength; i++) {
		mG.arcMatrix[arclist[i].pos1][arclist[i].pos2] = arclist[i].weight;
	}
}
//
int getpos(MGraph mG,VertexType v) {
	int pos = -1;
	int i = 0;
	while (i < mG.Vexnum) {
		if (mG.verList[i] == v) {
			pos = i;
			break;
		}
	}
	return pos;
}

 十八、编写迪杰斯特拉算法(不一定考)

算法思想:就是迪杰斯特拉算法的思想,大家在了解迪杰斯特拉算法后再来看就理解了.

//编写迪杰斯特拉算法
void Dijkstra(MGraph G, VertexType v, int dist[], int path[]) {
	int posv = getpos(G, v);
	if (posv == -1) {
		return;
	}
	int k = 0, min;
	bool s[MAX_VERTEX_NUM];
	for (int i = 0; i < G.Vexnum; i++) {
		s[i] = 0;
		dist[i] = G.arcMatrix[posv][i];
		if (dist[i] < INF || i == posv) {
			path[i] = posv;
		}
		else {
			path[i] = -1;
		}
	}
	dist[posv] = 0;
	s[posv] = 1;
	for (int i = 0; i < G.Vexnum - 1; i++) {
		min = INF;
		for (int j = 0; j < G.Vexnum; j++) {
			if (s[j] == 0 && min > dist[j]) {
				min = dist[j];
				k = j;
			}
		}
		s[k] = 1;
		for (int j = 0; j < G.Vexnum; j++) {
			if (s[j] == 0 && dist[j] > dist[k] + G.arcMatrix[k][j]) {
				dist[j] = dist[k] + G.arcMatrix[k][j];
				path[j] = k;
			}
		}
	}
}
void serchPre(MGraph G, int path[], int v, int k) {
	int m = path[k];
	if (m!= v) {
		serchPre(G, path, v, m);
	}
	printf("%d %c -> ",m, G.verList[m]);
}
void printpath(MGraph G, int dist[], int path[], VertexType v) {
	int posv = getpos(G, v);
	for (int i = 0; i < G.Vexnum; i++) {
		serchPre(G, path, posv, i);
		printf("%d %c\n",i, G.verList[i]);
		printf("长度为: %d\n", dist[i]);
	}
}

最终总代码和测试

大家可以直接复制我的代码运行一下之后边看代码边看结果都可以.

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<malloc.h>
#include<assert.h>
#define MAX_VERTEX_NUM 20
#define INFINITY -999999
//图的基本知识
//图的类型分为:
//有向图:带权值,不带权值

//无向图:带权值,不带权值

//以有向图为例
//图的数据结构有俩种:邻接表,临界矩阵

//定义图的邻接表的数据结构
//定义表结点的数据类型
typedef struct ArcNode {
	int adjVex;//终端节点
	struct ArcNode* nextArc;
	int weight;
}ArcNode;
//定义头节点的数据类型
typedef char VertexType;
typedef struct VNode {
	VertexType data;//顶点数据
	ArcNode* firstArc;//指向第一个表结点
	//AdjList是一个包含所有头结点的数组
}VNode,AdjList[MAX_VERTEX_NUM];

//定义图的临接表类型
typedef struct {
	AdjList vertices;
	int Vexnum;//总节点数
	int Arcnum;//总边数
	int Kind;//图的类型
	int MaxVexnum;
}ALGraph;//临界表类型

//定义图的邻接矩阵存储结构
typedef  struct MGraph {
	VertexType verList[MAX_VERTEX_NUM];
	int arcMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
	int Vexnum;
	int Arcnum;
	int Kind;
}MGraph;

//定义初始化图函数
void InitALGraph(ALGraph &G,int kind) {//kind表示是有向图还是无向图
	//由于我们定义了临接表的数据类型所以初始化比较简单
	for (int i = 0; i < MAX_VERTEX_NUM; i++) {
		G.vertices[i].firstArc = NULL;//这里只初始化了表节点的指针,数据暂时不用管
	}
	G.Vexnum = 0;
	G.Kind = kind;
	G.MaxVexnum = MAX_VERTEX_NUM;
	G.Arcnum = 0;
}
//定义插入表节点函数
void InsertVertex(ALGraph &G,VertexType v) {
	if (G.Vexnum >= G.MaxVexnum) {
		return;
	}
	G.vertices[G.Vexnum++].data = v;
}
//打印邻接表
void printALGraph(ALGraph G) {
	for (int i = 0; i < G.Vexnum; i++) {//遍历整个邻接表
		printf("%d %c -> ", i , G.vertices[i].data);
		ArcNode* p = G.vertices[i].firstArc;
		while (p != NULL) {
			printf("%d %c -> ",p->adjVex, G.vertices[p->adjVex].data);
			p = p->nextArc;
		}
		printf("NULL");
		printf("\n");
	}
	printf("图中有%d个节点,%d条边.\n", G.Vexnum, G.Arcnum);
}


//获取顶点的位置函数
int getVertexpos(ALGraph G, VertexType v) {
	for (int i = 0; i < G.Vexnum; i++) {//遍历表节点数组
		if (G.vertices[i].data == v) {
			return i;
		}
	}
	return -1;//顶点在表里不存在
}
//定义插入节点函数
void InsertArc(ALGraph& G, VertexType v1, VertexType v2) {
	int posv1 = getVertexpos(G, v1);//获取节点位置
	int posv2 = getVertexpos(G, v2);
	if (posv1 == -1 || posv2 == -1) {//判读两个节点是否都在图里
		printf("插入边的节点不存在,插入失败!!!!!!!\n");
		return;
	}
	else {
		//插入边前还需判断该是否存在该条边,这里就不在判断了,考试也不用写
		ArcNode* tmp = NULL;
		tmp = (ArcNode*)malloc(sizeof(ArcNode));
		assert(tmp);
		tmp->adjVex = posv2;//采用头插法插入节点
		tmp->nextArc = G.vertices[posv1].firstArc;
		G.vertices[posv1].firstArc = tmp;

		if (G.Kind == 0) {//无向图
			ArcNode* tmp = NULL;
			tmp = (ArcNode*)malloc(sizeof(ArcNode));
			assert(tmp);
			tmp->weight = 1;
			tmp->adjVex = posv1;
			tmp->nextArc = G.vertices[posv2].firstArc;
			G.vertices[posv2].firstArc = tmp;
		}
		G.Arcnum++;
	}
}
//定义删除边函数
void RemoveArc(ALGraph& G, VertexType v1, VertexType v2) {
	int posv1 = getVertexpos(G, v1);
	int posv2 = getVertexpos(G, v2);
	if (posv1 == -1 || posv2 == -1) {
		printf("删除边的节点不存在,插入失败!!!!!!!\n");
		return;
	}
	//链表节点删除一样
	ArcNode* pNode = G.vertices[posv1].firstArc;
	ArcNode* preNode = NULL;
	while (pNode != NULL && pNode->adjVex != posv2) {
		preNode = pNode;
		pNode = pNode->nextArc;
	}
	if (pNode != NULL) {//找到了该边
		if (preNode == NULL) {//该节点是第一个节点需要修改firstArc,或者直接判断pNode == G.vertices[posv1].firstArc;
			G.vertices[posv1].firstArc = pNode->nextArc;
		}
		else {//不是第一个节点
			preNode->nextArc = pNode->nextArc;
		}
		free(pNode);
		pNode = NULL;
	}
	else {
		printf("图中没有该边删除失败!!!!!!!!\n");
		return;
	}
	if (G.Kind == 0) {//由于在电脑上故可以在删除函数里判断,在手写时,可以在外面判断图的类型之后调用两次函数
		ArcNode* pNode = G.vertices[posv2].firstArc;
		ArcNode* preNode = NULL;
		while (pNode != NULL && pNode->adjVex != posv1) {
			preNode = pNode;
			pNode = pNode->nextArc;
		}
		if (pNode != NULL) {
			if (preNode == NULL) {
				G.vertices[posv2].firstArc = pNode->nextArc;
			}
			else {
				preNode->nextArc = pNode->nextArc;
			}
			free(pNode);
			pNode = NULL;
		}
		else {
			printf("图中没有该边删除失败!!!!!!!!\n");
			return;
		}
	}
	G.Arcnum--;
	printf("删除%c -> %c成功!\n", v1, v2);
	if (G.Kind == 0) {
		printf("删除%c -> %c成功!\n", v2, v1);
	}
}

//定义删除节点函数
//算法思想:将所有的关于删除节点的边,之后该节点保存邻接表左后一个节点的信息,然后将所有与最后一个节点有关的边的指向信息改为删除节点的位置
void RemoveVextex(ALGraph& G, VertexType vertex) {
	int posv = getVertexpos(G, vertex);
	if (posv == -1) {
		return;
	}
	//删除与vertex节点有关的所有边
	VertexType v;
	ArcNode* p = G.vertices[posv].firstArc;
	while (p != NULL) {
		v = G.vertices[p->adjVex].data;
		p = p->nextArc;
		RemoveArc(G, vertex, v);//删除边函数
	}
	//将最后的节点信息复制到删除节点的位置
	G.vertices[posv].firstArc = G.vertices[G.Vexnum - 1].firstArc;
	G.vertices[G.Vexnum - 1].firstArc = NULL;
	G.vertices[posv].data = G.vertices[G.Vexnum - 1].data;
	G.Vexnum--;
	//将所有有关最后一个节点的边,修改其指向位置为删除节点的位置
	ArcNode* s = NULL;
	p = G.vertices[posv].firstArc;
	while (p != NULL) {//遍历最后一个节点的边信息
		s = G.vertices[p->adjVex].firstArc;
		while (s != NULL && s->adjVex != G.Vexnum) {
			s = s->nextArc;
		}
		if (s != NULL) {
			s->adjVex = posv;//修改指向
		}
		p = p->nextArc;
	}
}
//定义销毁图函数
void DestroyGraph(ALGraph& G) {
	for (int i = G.Vexnum-1; i>=0; i--) {//从尾部删除
		RemoveVextex(G, G.vertices[i].data);
	}
	printf("销毁图成功!\n");
}
//定义获取第一个邻接顶点
int GetFirstNeighbor(ALGraph G, VertexType v) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return -1;//没有该节点
	}
	ArcNode* p = G.vertices[posv].firstArc;
	if (p != NULL) {//第一个节点为空
		return p->adjVex;
	}
	return -1;
}
//定义获取下一个邻接顶点
int GetNextNeighbor(ALGraph G, VertexType v1, VertexType v2) {//获取v1顶点v2后的下一个顶点
	int posv1 = getVertexpos(G, v1);
	int posv2 = getVertexpos(G, v2);
	if (posv1 == -1 || posv2 == -1) {
		return -1;
	}
	//找到v1到v2的边节点
	ArcNode* p = G.vertices[posv1].firstArc;
	while (p != NULL && p->adjVex != posv2) {
		p = p->nextArc;
	}
	//找到了且下一个节点不为空
	if (p != NULL && p->nextArc!=NULL) {
		return p->nextArc->adjVex;
	}
	return -1;
}
//定义创建测试图的函数
void creat(ALGraph &G) {
	InitALGraph(G, 0);
	InsertVertex(G, 'A');
	InsertVertex(G, 'B');
	InsertVertex(G, 'C');
	InsertVertex(G, 'D');
	InsertVertex(G, 'E');
	InsertArc(G, 'A', 'B');
	InsertArc(G, 'A', 'D');
	InsertArc(G, 'B', 'C');
	InsertArc(G, 'B', 'E');
	InsertArc(G, 'C', 'D');
	InsertArc(G, 'C', 'E');
}
//使用二维数组建立图
void creatALGraphArr(ALGraph& G, VertexType verList[], int vernum, char arcList[][2], int arcnum,int kind) {
	//基本信息一定要先初始化因为后面函数要用到基本信息
	G.Kind = kind;//建立该图的类型
	G.Vexnum = vernum;
	G.Arcnum = arcnum;
	G.MaxVexnum = MAX_VERTEX_NUM;
	//初始化表节点
	for (int i = 0; i < vernum; i++) {
		G.vertices[i].data = verList[i];//节点数据
		G.vertices[i].firstArc = NULL;//节点第一个指向的边节点为NULL
	}
	//插入边节点
	for (int i = 0; i < arcnum; i++) {
		VertexType v1 = arcList[i][0];
		VertexType v2 = arcList[i][1];
		int posv1 = getVertexpos(G, v1);
		int posv2 = getVertexpos(G, v2);
		if (posv1 == -1 || posv2 == -1) {
			printf("边的节点不在邻接表!失败!!!!!\n");
			break;
		}
		ArcNode* pNode = (ArcNode*)malloc(sizeof(ArcNode));
		assert(pNode);
		pNode->weight = 1;
		pNode->adjVex = posv2;
		//头插法
		pNode->nextArc = G.vertices[posv1].firstArc;
		G.vertices[posv1].firstArc = pNode;
		//无向图两个节点都要插入
		if (G.Kind == 0) {
			ArcNode* pNode = (ArcNode*)malloc(sizeof(ArcNode));
			assert(pNode);
			pNode->adjVex = posv1;
			//头插法
			pNode->nextArc = G.vertices[posv2].firstArc;
			G.vertices[posv2].firstArc = pNode;
		}
	}
}
//将邻接表存储的有向图G转换成逆邻接表存储
void reverseALGraph(ALGraph G, ALGraph& rG) {
	rG.MaxVexnum = MAX_VERTEX_NUM;
	rG.Arcnum = 0;
	rG.Kind = G.Kind;
	rG.Vexnum = G.Vexnum;
	//复制表节点
	for (int i = 0; i < G.Vexnum; i++) {
		rG.vertices[i].data = G.vertices[i].data;
		rG.vertices[i].firstArc = NULL;//头节点指针域制空
	}
	for (int i = 0; i < G.Vexnum; i++) {
		VertexType v1 = G.vertices[i].data;
		ArcNode* p = G.vertices[i].firstArc;
		while (p != NULL) {
			VertexType v2 = G.vertices[p->adjVex].data;
			InsertArc(rG, v2, v1);
			p = p->nextArc;
		}
	}
}
//设计算法计算有向图的所有顶点的度
//算法思想:有向图的度只需遍历所有边遇到一个边弧头和弧尾的入度加一
void GetDegreedVertex(ALGraph G,int degree[]) {
	for (int i = 0; i < G.Vexnum; i++) {
		ArcNode* pNode = G.vertices[i].firstArc;
		while (pNode != NULL) {
			degree[i]++;
			degree[pNode->adjVex]++;
			pNode = pNode->nextArc;
		}
	}
}

//将邻接表表示的有向网转换成邻接矩阵(有向网带权值默认权值都为1)
#define INF 999999
void convertAdjList(ALGraph G, MGraph& mG) {
	mG.Arcnum = G.Arcnum;
	mG.Vexnum = G.Vexnum;
	mG.Kind = G.Kind;
	//初始化邻接矩阵
	for (int i = 0; i < G.Vexnum; i++) {
		for (int j = 0; j < G.Vexnum; j++) {
			mG.arcMatrix[i][j] = INF;
		}
	}
	//遍历邻接表转换成邻接矩阵
	for (int i = 0; i < G.Vexnum; i++) {
		mG.verList[i] = G.vertices[i].data;
		ArcNode* pNode = G.vertices[i].firstArc;
		while (pNode != NULL) {
			int posv1 = i;
			int posv2 = pNode->adjVex;
			mG.arcMatrix[posv1][posv2] = pNode->weight;
			pNode = pNode->nextArc;
		}
	}
}
//定义打印邻接矩阵函数
void printMGraph(MGraph mG) {
	printf(" ");
	for (int i = 0; i < mG.Vexnum; i++) {
		printf("%10.c ", mG.verList[i]);
	}
	printf("\n");
	for (int i = 0; i < mG.Vexnum; i++) {
		printf("%c ", mG.verList[i]);
		for (int j = 0; j < mG.Vexnum; j++) {
			printf("%10.d ", mG.arcMatrix[i][j]);
		}
		printf("\n");
	}
	printf("该邻接矩阵有%d个节点,%d条边\n", mG.Vexnum, mG.Arcnum);
}

//图的广度优先遍历(BFS)(这是解决图基本问题的基本算法,一定要理解并应用)
//算法思想:图的广度优先遍历类似与树的层序遍历,借助队列辅助完成,要借助visited数组
void BFS(ALGraph G,VertexType v,int visited[]){
	int posv = getVertexpos(G, v);
	if (posv == -1) {//顶点 不在邻接表里
		return;
	}
	printf("%c ", v);
	visited[posv] = 1;
	//定义辅助数组队列
	int Queue[40] = { 0 };//注意这里只申请了40空间
	int front = 0;
	int rear = 0;
	Queue[++rear] = posv;
	while (front != rear) {
		int postmp = Queue[++front];
		ArcNode* pNode = NULL;
		for (pNode = G.vertices[postmp].firstArc; pNode != NULL; pNode = pNode->nextArc) {
			int adj = pNode->adjVex;
			if (visited[adj] == 0) {//邻接的顶点没有访问.进队
				printf("%c ", G.vertices[adj].data);
				visited[adj] = 1;
				Queue[++rear] = adj;
			}
		}
	}
}

void BFSTraverse(ALGraph G) {
	int visited[MAX_VERTEX_NUM];
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	for (int i = 0; i < G.Vexnum; i++) {
		if (visited[i] == 0) {
			BFS(G, G.vertices[i].data, visited);
		}
	}
	printf("\n");
}
//图的深度优先遍历(DFS)(这是解决图基本问题的基本算法,一定要理解并应用)
//算法思想:图的深度优先遍历类于树的三种遍历方式,应用递归,要借助visited数组
void DFS(ALGraph G, VertexType v, int visited[]) {
	int posv = getVertexpos(G, v);
	printf("%c ", v);
	visited[posv] = 1;
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			DFS(G, G.vertices[adj].data, visited);
		}
		pNode = pNode->nextArc;
	}
}

void DFSTraverse(ALGraph G) {
	int visited[MAX_VERTEX_NUM];
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	for (int i = 0; i < G.Vexnum; i++) {
		if (visited[i] == 0) {
			DFS(G, G.vertices[i].data, visited);
		}
	}
	printf("\n");
}
//判断以邻接表为存储结构的有向图G是否存在环
//算法思想:以深度优先遍历为思想,设置顶点访问状态为0:未访问,1:正在访问,2:访问完成,如果访问的过程中访问到正在访问的顶点则说明有环
int DFSTraversing(ALGraph G, VertexType v,int visited[]) {
	int ret = 0;
	int posv = getVertexpos(G, v);
	visited[posv] = 1;
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			ret = DFSTraversing(G, G.vertices[adj].data, visited);
		}
		else if (visited[adj] == 1) {
			return 1;
		}
		if (ret == 1) {
			return 1;
		}
		pNode = pNode->nextArc;
	}
	visited[posv] = 2;
	return 0;
}

void isExistRing(ALGraph G) {
	int visited[MAX_VERTEX_NUM];
	int ret = 0;
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	for (int i = 0; i < G.Vexnum; i++) {
		if (visited[i] == 0) {
			ret = DFSTraversing(G, G.vertices[i].data, visited);
			if (ret == 1) {
				printf("%d has ring!\n",ret);
				break;
			}
		}
	}
	if (ret == 0) {
		printf("hasn't ring !\n");
	}
}
//编写算法判断以邻接表方式存储的有向图G是否存在srcVertex到destVertex的路径
//算法思想:以深度优先遍历为思想,如果访问的过程中访问到了destVertex那么就说明存在路径
int DFSTraversing2(ALGraph G,VertexType v,VertexType destVertex,int visited[]) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return 0;
	}
	visited[posv] = 1;
	if (v == destVertex) {//如果当前访问顶点就是目标顶点,找到了,返回
		return 1;
	}
	int  ret = 0;
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {//向邻接顶点寻找
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			ret = DFSTraversing2(G, G.vertices[adj].data, destVertex, visited);
		}
		if (ret == 1) {//找到了返回
			return 1;
		}
		pNode = pNode->nextArc;
	}
	return 0;
}

void isExistPath(ALGraph G,VertexType srcVertex,VertexType destVertex) {
	int visited[MAX_VERTEX_NUM];
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	int ret = 0;
	ret = DFSTraversing2(G, srcVertex, destVertex, visited);//这里只调用一次DFS就可以了
	if (ret == 1) {
		printf("%c 到 %c 存在路径!\n",srcVertex,destVertex);
	}
	else {
		printf("%c 到 %c 不存在路径!\n", srcVertex, destVertex);
	}
}
//设计算法求出以邻接表存储的有向图中所有从顶点v到w的简单路径
//算法思想:还是以深度优先遍历为思想,与判断存在路径有异曲同工之妙
void printVertexList(VertexType verlist[], int verlength) {
	for (int i = 0; i < verlength; i++) {
		printf("%c ", verlist[i]);
	}
	printf("\n");

}
void DFSTraversing3(ALGraph G,VertexType v,VertexType w,int visited[],VertexType verList[],int &verlength) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return;
	}
	visited[posv] = 1;
	verList[verlength++] = v;
	if (v == w) {//找到目标节点打印路径
		printVertexList(verList, verlength);
	}
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			DFSTraversing3(G, G.vertices[adj].data, w, visited, verList, verlength);
		}
		pNode = pNode->nextArc;
	}
	visited[posv] = 0;//退出访问寻找其他路径
	verlength--;
}

void getPath(ALGraph G,VertexType src,VertexType dest) {
	int visited[MAX_VERTEX_NUM];
	VertexType verlist[MAX_VERTEX_NUM];
	int verlength = 0;
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	printf("%c 到 %c 的路径有\n",src,dest);
	DFSTraversing3(G, src, dest, visited, verlist, verlength);
}
//设计算法求解以邻接表存储de有向图G中所有从顶点v到顶点w长度为d的路径
//算法思想:还是以深度优先遍历的思想,与上面的算法异曲同工之妙
void DFSTraversing4(ALGraph G, VertexType v, VertexType w, int visited[], VertexType verList[], int& verlength, int distant) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return;
	}
	verList[verlength++] = v;
	visited[posv] = 1;
	if (v == w && distant == 0) {
		printVertexList(verList, verlength);
	}
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			DFSTraversing4(G, G.vertices[adj].data, w, visited, verList, verlength, distant-1);
		}
		pNode = pNode->nextArc;
	}
	visited[posv] = 0;
	verlength--;
}
void getPathdistant(ALGraph G, VertexType src, VertexType dest,int distant) {
	int visited[MAX_VERTEX_NUM];
	VertexType verlist[MAX_VERTEX_NUM];
	int verlength = 0;
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	printf("%c 到 %c 的路径长度为%d的路径有\n", src, dest,distant);
	DFSTraversing4(G, src, dest, visited, verlist, verlength,distant);
}
//设计算法对有向无环图进行拓扑排序(AOV网)
//算法思想:对图进行深度优先遍历为逆拓扑排序
void DFSTraversing5(ALGraph G,VertexType v,int visited[] ,VertexType verlist[],int &verlength) {
	int posv = getVertexpos(G, v);
	if (posv == -1) {
		return;
	}
	visited[posv] = 1;
	ArcNode* pNode = G.vertices[posv].firstArc;
	while (pNode != NULL) {
		int adj = pNode->adjVex;
		if (visited[adj] == 0) {
			DFSTraversing5(G, G.vertices[adj].data, visited, verlist, verlength);
		}
		pNode = pNode->nextArc;
	}
	verlist[verlength++] = v;
}

void printlogicsort(VertexType verlist[],int verlength) {
	printf("拓扑排序的序列为:");
	for (int i = verlength - 1; i >= 0; i--) {
		printf("%c ", verlist[i]);
	}
	printf("\n");
}
void getlogicsort(ALGraph G) {
	int visited[MAX_VERTEX_NUM];
	VertexType verlist[MAX_VERTEX_NUM];
	int verlength = 0;
	for (int i = 0; i < G.Vexnum; i++) {
		visited[i] = 0;
	}
	for (int i = 0; i < G.Vexnum; i++) {
		if (visited[i] == 0) {
			DFSTraversing5(G, G.vertices[i].data, visited, verlist, verlength);
		}
	}
	printlogicsort(verlist, verlength);
}
//创建以邻接矩阵为存储结构的有向图
typedef struct arc {
	int pos1;
	int pos2;
	int weight;
}arc,ArcList[MAX_VERTEX_NUM];

void creatMGraph(MGraph &mG,VertexType verlist[],int verlength,ArcList arclist,int arclength) {
	mG.Vexnum = verlength;
	mG.Arcnum = arclength;
	mG.Kind = 1;
	for (int i = 0; i < verlength; i++) {
		mG.verList[i] = verlist[i];
	}
	for (int i = 0; i < mG.Vexnum; i++) {
		for (int j = 0; j < mG.Vexnum; j++) {
			mG.arcMatrix[i][j] = INF;
		}
	}
	for (int i = 0; i < arclength; i++) {
		mG.arcMatrix[arclist[i].pos1][arclist[i].pos2] = arclist[i].weight;
	}
}
//
int getpos(MGraph mG,VertexType v) {
	int pos = -1;
	int i = 0;
	while (i < mG.Vexnum) {
		if (mG.verList[i] == v) {
			pos = i;
			break;
		}
	}
	return pos;
}

//编写迪杰斯特拉算法
void Dijkstra(MGraph G, VertexType v, int dist[], int path[]) {
	int posv = getpos(G, v);
	if (posv == -1) {
		return;
	}
	int k = 0, min;
	bool s[MAX_VERTEX_NUM];
	for (int i = 0; i < G.Vexnum; i++) {
		s[i] = 0;
		dist[i] = G.arcMatrix[posv][i];
		if (dist[i] < INF || i == posv) {
			path[i] = posv;
		}
		else {
			path[i] = -1;
		}
	}
	dist[posv] = 0;
	s[posv] = 1;
	for (int i = 0; i < G.Vexnum - 1; i++) {
		min = INF;
		for (int j = 0; j < G.Vexnum; j++) {
			if (s[j] == 0 && min > dist[j]) {
				min = dist[j];
				k = j;
			}
		}
		s[k] = 1;
		for (int j = 0; j < G.Vexnum; j++) {
			if (s[j] == 0 && dist[j] > dist[k] + G.arcMatrix[k][j]) {
				dist[j] = dist[k] + G.arcMatrix[k][j];
				path[j] = k;
			}
		}
	}
}
void serchPre(MGraph G, int path[], int v, int k) {
	int m = path[k];
	if (m!= v) {
		serchPre(G, path, v, m);
	}
	printf("%d %c -> ",m, G.verList[m]);
}
void printpath(MGraph G, int dist[], int path[], VertexType v) {
	int posv = getpos(G, v);
	for (int i = 0; i < G.Vexnum; i++) {
		serchPre(G, path, posv, i);
		printf("%d %c\n",i, G.verList[i]);
		printf("长度为: %d\n", dist[i]);
	}
}






int main() {
	ALGraph G;
	creat(G);
	printALGraph(G);
	//删除边
	RemoveArc(G, 'B', 'C');
	//RemoveArc(G, 'A', 'C');//图中没有该条边删除失败
	printALGraph(G);
	ALGraph G1;
	creat(G1);
	printALGraph(G1);
	RemoveVextex(G1, 'C');
	printALGraph(G1);
	DestroyGraph(G);
	printALGraph(G);
	printf("G表以被摧毁,请不要再使用,如使用请重新创建.\n");
	printf("重新创建G表\n");
	creat(G);
	printALGraph(G);
	printf("获取图G中节点%c的位置为:%d\n",'A',GetFirstNeighbor(G,'A'));
	printf("获取图G中节点 %c到 %c 的下一个节点位置为:%d\n", 'B', 'E',GetNextNeighbor(G,'B','E'));
	printf("使用二维数组建立邻接表.\n");
	char verList[5] = { 'A','B','C','D','E' };
	char arcList[][2] = { {'A', 'B'},{'A', 'D'},{'B', 'C'},{'B', 'E'},{'C', 'D'},{'C', 'E'} };
	int vernum = 5;
	int arcnum = 6;
	int kind = 0;
	ALGraph G2;
	creatALGraphArr(G2, verList, vernum, arcList, arcnum, kind);
	printALGraph(G2);
	printf("创建一个有向图的邻接表!\n");
	ALGraph G3,G4;
	creatALGraphArr(G3, verList, vernum, arcList, arcnum, 1);
	printALGraph(G3);
	reverseALGraph(G3, G4);
	printALGraph(G4);
	int degree[5] = { 0 };
	GetDegreedVertex(G3, degree);
	for (int i = 0; i < 5; i++) {
		printf("%c顶点的度为:%d\n", G.vertices[i].data, degree[i]);
	}
	printf("将邻接表转换成邻接矩阵\n");
	printALGraph(G3);
	MGraph mG;
	convertAdjList(G3, mG);
	printMGraph(mG);
	printf("对图G进行广度优先遍历.\n");
	printALGraph(G);
	BFSTraverse(G);
	printf("对图G1进行广度优先遍历.\n");
	printALGraph(G1);
	BFSTraverse(G1);
	printf("对图G进行深度优先遍历.\n");
	printALGraph(G);
	DFSTraverse(G);
	printf("对图G1进行深度优先遍历.\n");
	printALGraph(G1);
	DFSTraverse(G1);
	printf("判断图G是否存在回路\n");
	isExistRing(G);
	printf("判断G3存在路径!\n");
	printALGraph(G3);
	isExistPath(G3, 'A', 'E');
	isExistPath(G3, 'B', 'D');
	isExistPath(G3, 'C', 'A');
	printf("打印G3路径!\n");
	getPath(G3, 'A', 'E');
	getPath(G3, 'B', 'E');
	getPath(G3, 'C', 'A');//没有路径
	printf("+++++++++++++++++++++++++++++\n");
	getPathdistant(G3, 'A', 'E', 3);
	getPathdistant(G3, 'B', 'E', 1);
	getPathdistant(G3, 'B', 'E', 2);
	getPathdistant(G3, 'C', 'A', 2);
	printf("+++++++++++++++++++++++++++++\n");
	printf("对图G3进行拓扑排序!\n");
	getlogicsort(G3);
	printf("应用迪杰斯特拉算法求解单源最短路径问题!\n");
	MGraph mG1;
	VertexType verlist[5] = { 'A','B','C','D','E' };
	int verlength = 5;
	ArcList arclist = { {0,1,10},{0,4,5},{1,2,1},{1,4,2},{2,3,4},{3,0,7},{3,2,6},{4,1,3},{4,2,9},{4,3,2} };
	int arclength = 10;
	creatMGraph(mG1, verlist, verlength, arclist, arclength);
	printMGraph(mG1);
	int path[MAX_VERTEX_NUM];
	int dist[MAX_VERTEX_NUM];

	Dijkstra(mG1, 'A', dist, path);
	printf("path数组:");
	for (int i = 0; i < mG1.Vexnum; i++) {
		printf("%d ", path[i]);
	}
	printf("\n");
	printf("dist数组:");
	for (int i = 0; i < mG1.Vexnum; i++) {
		printf("%d ", dist[i]);
	}
	printf("\n");
	printpath(mG1, dist, path, 'A');
	return 0;
}

 

 

---

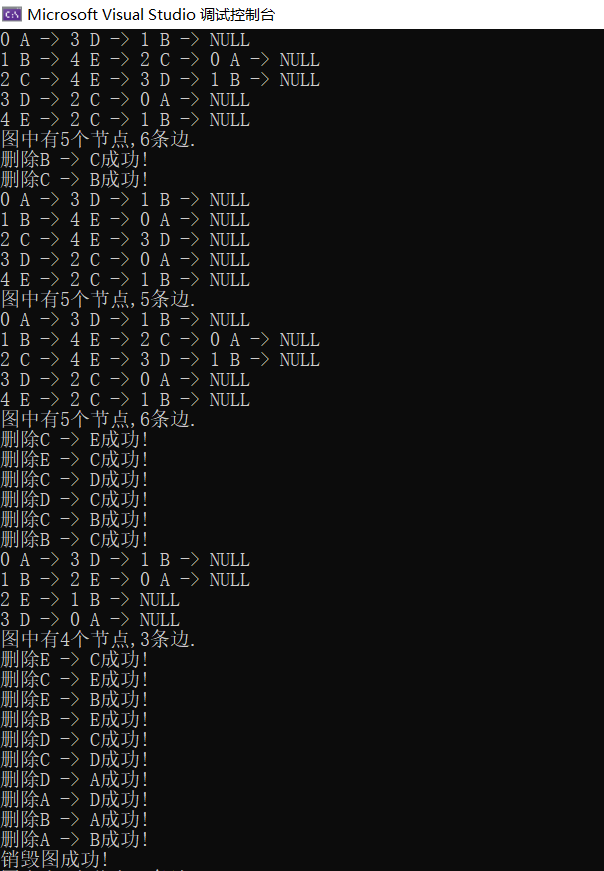
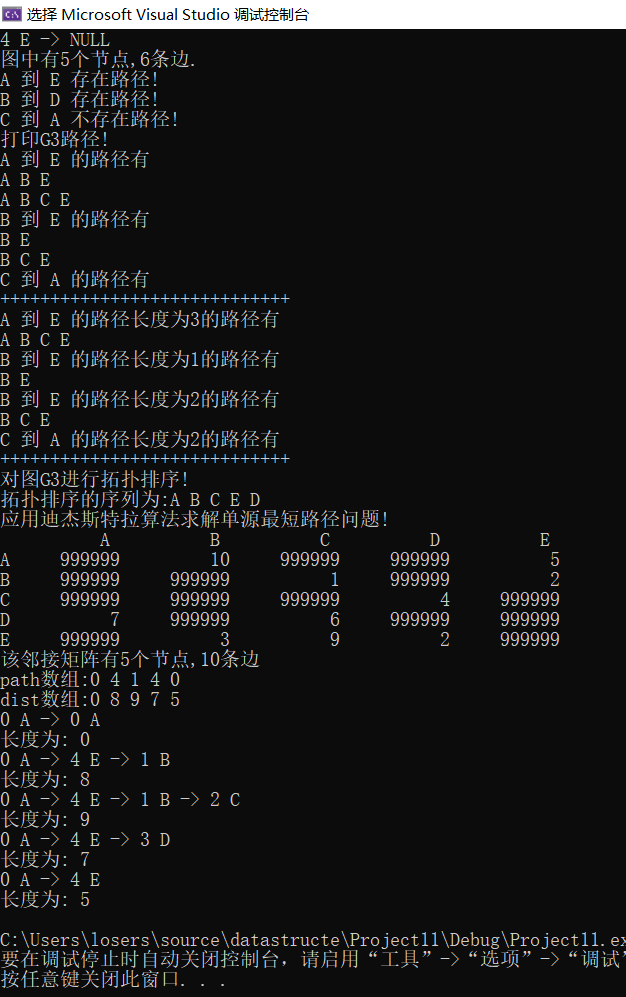
总结

感觉自己也没有太讲直接将代码就粘到这里了,在这里不好意思对不起大家了,有的代码中有注释还有算法思想都是自己总结出来的,图这块的内容还是比较多的,但最终还是基本算法的演变,加油各位朋友.