目录
拆分单词 牛客题霸_牛客网
【思路梳理】
剑指 Offer II 100. 三角形中最小路径之和
【解法一】自顶向下
【解法二】自底向上
路径的数目 剑指 Offer II 098. 路径的数目
【解法一】
【解法二】
路径的数目(加入障碍物)63. 不同路径 II
【解法一】原数组上进行操作(空间换时间……)
【解法二】优化版
拆分单词

【思路梳理】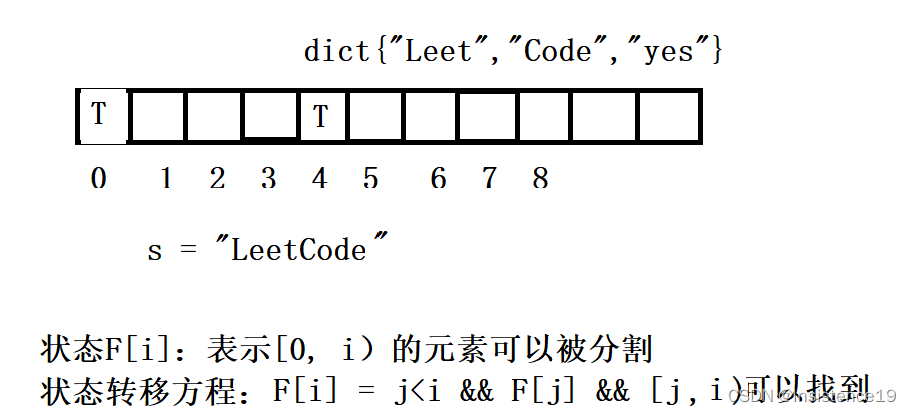



class Solution {
public:
bool wordBreak(string s, unordered_set<string> &dict) {
vector<bool> res(s.size()+1, false);
res[0] = true;
for(int i = 1; i <= s.size(); i++)
{
for(int j = i-1; j >=0; --j)
{
if(res[j] && dict.find(s.substr(j,i-j))!=dict.end())
{
res[i] = true;
break;
}
}
}
return res[s.size()];
}
};【解法一】自顶向下
状态:F[i,j] 表示从【0,0】到【i,j】的最小路径和
状态转移方程为:
初始条件:F[0,0] = array[0][0]
返回结果min(F[row-1,j);
思想划分:
① 更新三角形的俩条边,对于斜边来说只能是从前一个到后一个,所以数值更新为前一个加上自身元素值。
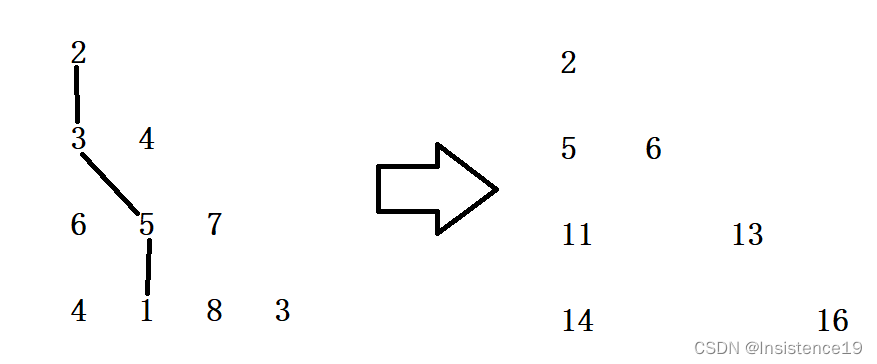
② 更新三角形内部元素,从第三行第二列开始,将值更新为前一行本列与前一行前一列的最小值加上当前值
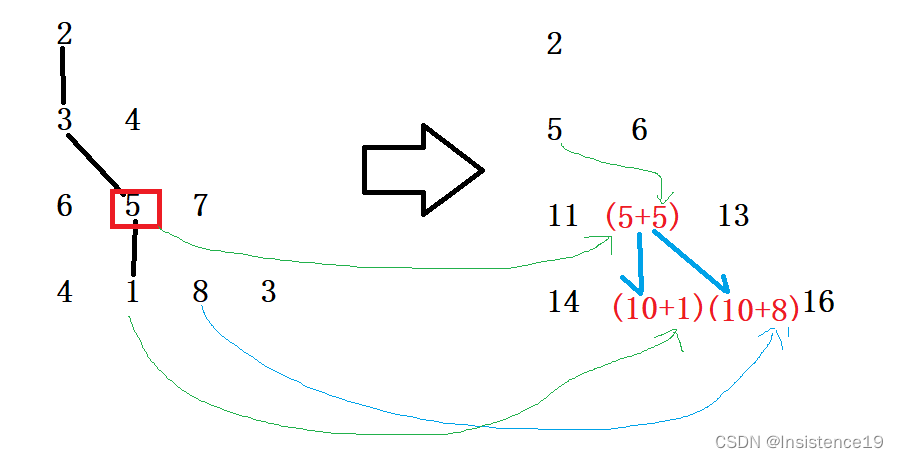
③ 找到最后一行中最小的元素值(11即为所求)
class Solution {
public:
int minimumTotal(vector<vector<int> > &triangle) {
int row = triangle.size();
int col = triangle[row-1].size();
// 1、初始化三角形的俩个斜边
for(int i = 1; i < row; ++i)
{
for(int j = 0; j < triangle[i].size(); j++)
{
if(j==0)
{
triangle[i][j] = triangle[i-1][j] + triangle[i][j];
}
else if(i==j)
{
triangle[i][j] = triangle[i-1][j-1] + triangle[i][j];
}
}
}
// 2、初始化三角形内部元素
for(int i = 2; i < row; ++i)
{
for(int j = 1; j < triangle[i].size()-1; j++)
{
triangle[i][j] = min(triangle[i-1][j], triangle[i-1][j-1])+triangle[i][j];
}
}
// 3、找到初始化之后三角形最后一行中最小的元素
int min = triangle[row-1][0];
for(int j = 1; j < triangle[row-1].size(); ++j)
{
if(triangle[row-1][j]<min)
min = triangle[row-1][j];
}
return min;
}
};【解法二】自底向上
状态F[i,j] 从【i,j】到 最底行的最小路径和
状态转移方程F[i,j] = min(F[i+1,j], F[i+1, j+1]) + array[i][j]
初始状态 F[row-1, j] = array[row-1][j]
返回结果 F[0, 0]
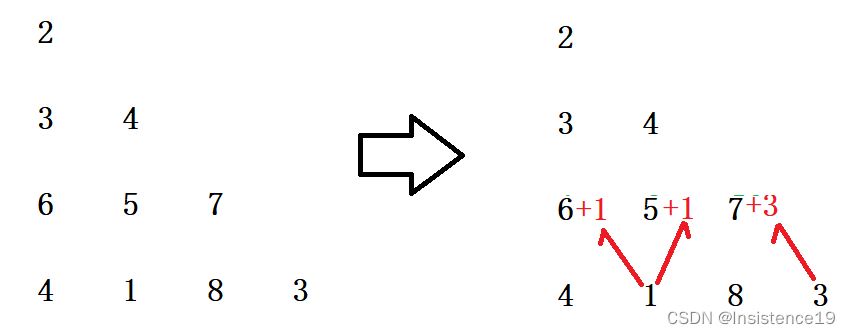

class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
// F[i,j] = triangle[row-1][j]
int row = triangle.size();
for(int i = row-2; i >= 0; --i)
{
for(int j = 0; j < triangle[i].size(); ++j)
{
triangle[i][j] = min(triangle[i+1][j],triangle[i+1][j+1])+
triangle[i][j];
}
}
return triangle[0][0];
}
};路径的数目
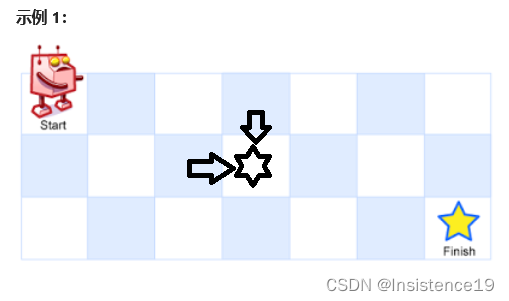
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
【思路梳理】

【解法一】
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> res(m, vector<int> (n, 1));
for(int i = 1; i < m; i++)
for(int j = 1; j < n; j++)
res[i][j] = res[i-1][j] + res[i][j-1];
return res[m-1][n-1];
}
};【解法二】
vector<vector<int>> res(m, vector<int> (n,0));
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(i==0&&j==0)
res[i][j]=1;
else
{
if(i)res[i][j] += res[i-1][j];
if(j)res[i][j] += res[i][j-1];
}
}
}
return res[m-1][n-1];路径的数目(加入障碍物)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
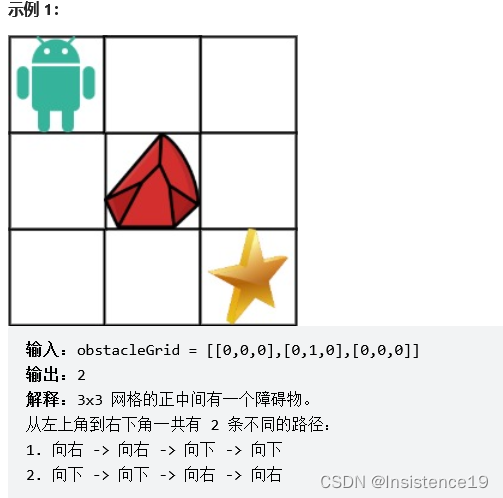
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
【解法一】原数组上进行操作(空间换时间……)
1、对终点和起点有无障碍物的判断
2、在原数组上将障碍物置为-1
将第一行和第一列不为障碍物的元素置为1
如果第一行或第一列有障碍物,就将其后续元素全部置为-1
3、对数组其余元素进行访问
注意对出口的俩个方向都为障碍物的判断
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& res) {
int row = res.size();
int col = res[0].size();
// 1、对终点和起点有无障碍物的判断
if(res[row-1][col-1]==1||res[0][0]==1)
return 0;
res[row-1][col-1] = 0;
// 2、在原数组上将障碍物置为-1
// 将第一行和第一列不为障碍物的元素置为1
// 如果第一行或第一列有障碍物,就将其后续元素全部置为-1
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
if(res[i][j]==0)
{
if(i==0 || j==0)
res[i][j] = 1;
}
else
res[i][j] = -1;
}
}
for(int i = 1; i < row; i++)
{
if(res[i][0]==-1)
{
i++;
while(i<row)
{
res[i++][0]=-1;
}
break;
}
}
for(int j = 1; j < col; j++)
{
if(res[0][j]==-1)
{
j++;
while(j<col)
{
res[0][j++]=-1;
}
break;
}
}
// 3、对数组其余元素进行访问
// 注意对出口的俩个方向都为障碍物的判断
for (int i = 1; i < row; i++)
{
for (int j = 1; j < col; j++)
{
if (res[i][j] == -1)
{
continue;
}
else
{
if(i==row-1&&j==col-1&&res[i - 1][j] == -1 && res[i][j - 1] == -1)
{
return 0;
}
else if (res[i - 1][j] == -1 && res[i][j - 1] == -1)
res[i][j] = -1;
else if (res[i - 1][j] == -1)
res[i][j] = res[i][j - 1];
else if (res[i][j - 1] == -1)
res[i][j] = res[i - 1][j];
else
res[i][j] = res[i - 1][j] + res[i][j - 1];
}
}
}
return res[row-1][col-1];
}
};【解法二】优化版
用0填充新开辟一个数组,省去了上述第二步诸多操作
1、首先进行正常的出入口都是障碍物的判断
2、新建数组并且全部赋值为0的好处就是不用对第一行第一列进行遇到障碍物就要清除后续路径的操作
3、直接用下标访问路径上没有障碍物的路径,从0,0下标一路出发,对每个不是障碍物的结点进行赋值,利用俩个if判断i j是否为零,如果不是第一行,那么就可以从上方来,如果不是第一列就可以从左边来。
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& o) {
int m = o.size();
int n = o[0].size();
if(o[m-1][n-1]==1 || o[0][0]==1)
return 0;
vector<vector<int>> res(m, vector<int> (n, 0));
res[0][0] = 1;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(o[i][j]==0)
{
if(i)res[i][j] += res[i-1][j];
if(j)res[i][j] += res[i][j-1];
}
}
}
return res[m-1][n-1];
}
};









![[ins 2022] 针对已见和未见群体的群体推荐中的贝叶斯归纳学习](https://img-blog.csdnimg.cn/img_convert/cb39c564d59d5b69d21660db8aadd50a.jpeg)
