1143. 最长公共子序列 (medium)
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。示例 1:
输入:text1 = “abcde”, text2 = “ace”
输出:3
解释:最长公共子序列是 “ace” ,它的长度为 3 。
示例 2:输入:text1 = “abc”, text2 = “abc”
输出:3
解释:最长公共子序列是 “abc” ,它的长度为 3 。
示例 3:输入:text1 = “abc”, text2 = “def”
输出:0
解释:两个字符串没有公共子序列,返回 0 。提示:
1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。
方法1:动态规划

-
思路:注意子序列可以不连续
-
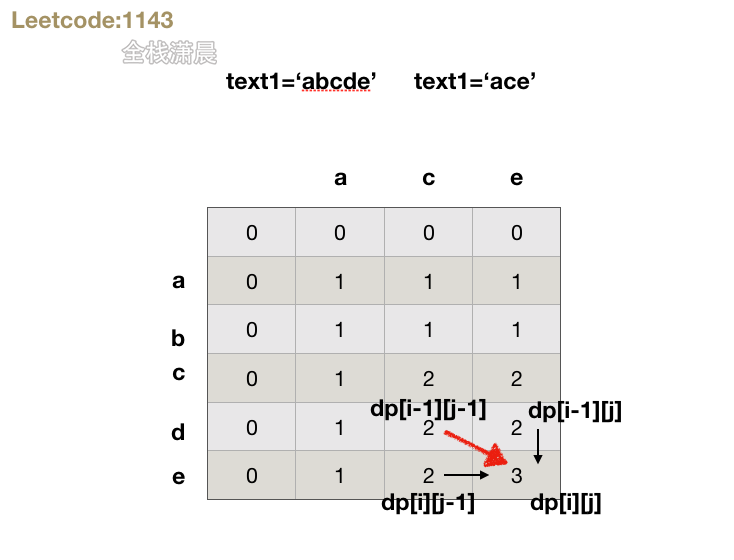
状态定义:
dp[i][j]表示text1[0:i-1]和text2[0:j-1]的最长公共子序列,注意是闭区间,之所以是到i-1或j-1,是方便初始化dp数组,当i=0或者j=0的时候表示的就是空字符和另一个字符串匹配,此时的dp[i][j]=0 -
状态转移方程:当
text1[i - 1] == text2[j - 1]时:dp[i][j] = dp[i - 1][j - 1] + 1当
text1[i - 1] != text2[j - 1]时:dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); -
dp的初始化:当 i = 0 时:
dp[0][j]=0当
j = 0时:dp[i][0]=0 -
返回结果:
dp[len(text1)][len(text2)]
-
-
复杂度:时间复杂度
O(mn),空间复杂度O(mn)
js:
var longestCommonSubsequence = function(text1, text2) {
const m = text1.length, n = text2.length;
const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));//初始化dp
for (let i = 1; i <= m; i++) {
const c1 = text1[i - 1];
for (let j = 1; j <= n; j++) {
const c2 = text2[j - 1];
if (c1 === c2) {
dp[i][j] = dp[i - 1][j - 1] + 1;//text1与text2字符相同时 最长公共子序列长度+1
} else {
//text1与text2字符不同时 返回text1或text2向前减少一位之后的最长公共子序列中的较大者
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
};
844. 比较含退格的字符串 (easy)
给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。
注意:如果对空文本输入退格字符,文本继续为空。
示例 1:
输入:s = “ab#c”, t = “ad#c”
输出:true
解释:s 和 t 都会变成 “ac”。
示例 2:输入:s = “ab##”, t = “c#d#”
输出:true
解释:s 和 t 都会变成 “”。
示例 3:输入:s = “a#c”, t = “b”
输出:false
解释:s 会变成 “c”,但 t 仍然是 “b”。提示:
1 <= s.length, t.length <= 200
s 和 t 只含有小写字母以及字符 ‘#’

方法1.截取字符串,循环字符串,遇到#就截掉最后一个字符,循环完毕之后,最后比较两个去除掉#退格之后的字符串是否相等,时间复杂度O(m+n),m、n是两个字符串的长度。空间复杂度O(1)
方法2.双指针
- 思路:双指针从右往左循环,每次循环两个字符处理掉#,直到第一个字符是右边退格全部处理掉之后的字符,然后看这两个字符是否一致
- 复杂度:时间复杂度
O(m+n),m、n是两个字符串的长度。空间复杂度O(1)
js:
var backspaceCompare = function(S, T) {
let i = S.length - 1,
j = T.length - 1,
skipS = 0,
skipT = 0;
//双指针从右往左循环
while(i >= 0 || j >= 0){
while(i >= 0){//处理掉# 直到left指向的字符右边退格全部处理掉
if(S[i] === '#'){
skipS++;
i--;
}else if(skipS > 0){
skipS--;
i--;
}else break;
}
while(j >= 0){//处理掉# 直到right指向的字符右边退格全部处理掉
if(T[j] === '#'){
skipT++;
j--;
}else if(skipT > 0){
skipT--;
j--;
}else break;
}
if(S[i] !== T[j]) return false;//如果处理掉退格之后的字符串不相等,返回false
i--;//继续循环
j--;
}
return true;//如果循环过程中没返回false 最后就返回true
};
301. 删除无效的括号 (hard)
给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。
示例 1:
输入:s = “()())()”
输出:[“(())()”,“()()()”]
示例 2:输入:s = “(a)())()”
输出:[“(a())()”,“(a)()()”]
示例 3:输入:s = “)(”
输出:[“”]提示:
1 <= s.length <= 25
s 由小写英文字母以及括号 ‘(’ 和 ‘)’ 组成
s 中至多含 20 个括号
方法1:bfs
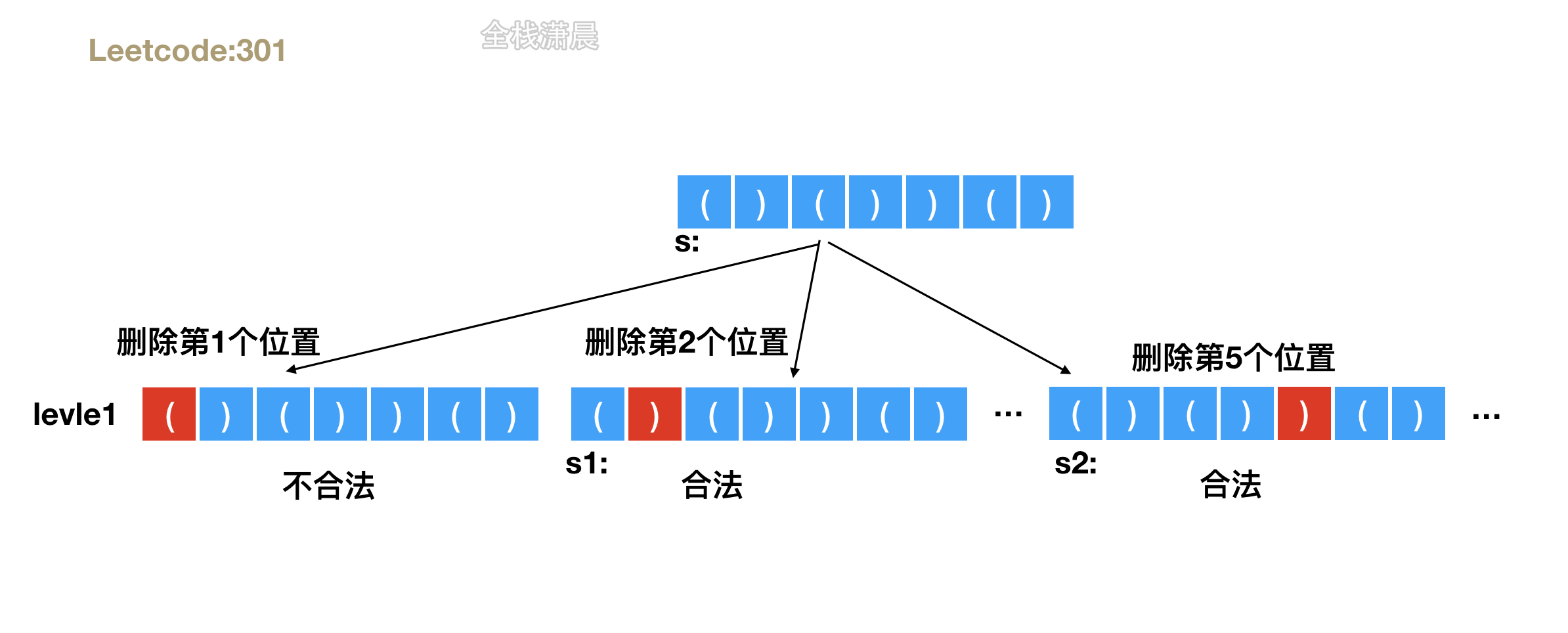
- 思路:最少删除的括号数量,这种求最短或者最少的题目,联想到bfs,bfs第一个出现解的层,即为最短删除括号所形成的合法字符串。准备queue对字符串进行bfs搜索,出现合法字符串入队,否则尝试删除一个字符,进入下一层判断,注意合法字符可能重复,需要去重。
js:
var removeInvalidParentheses = function (s) {
let res = [];
let queue = [];
let visited = new Set();//去重
queue.push(s);
while (true) {
let size = queue.length;//[s]
for (let i = 0; i < size; i++) {
s = queue.shift();//出队
if (isVaild(s)) {//如果是合法字符串
res.push(s);//加入结果数组
} else if (res.length == 0) {//不合法并且res.length == 0 则进入bfs下一层 尝试删除字符
for (let i = 0; i < s.length; i++) {
if (s[i] == '(' || s[i] === ')') {//是左右括号尝试删除字符,否则跳过
let nexts = s.substring(0, i) + s.substring(i + 1);
if (!visited.has(nexts)) {//判断新生成的字符串是否重复
queue.push(nexts);//加入队列 进入下一层 [s1,s2...]
visited.add(nexts);//加入去重数组
}
}
}
}
}
if (res.length > 0) {//出现合法字符串的那一层,终止循环
break;
}
}
return res;
};
function isVaild(s) {
let count = 0;
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {//左括号count+1
count++;
} else if (s[i] === ')') {//右括号count-1
count--;
}
if (count < 0) {//小于0 说明右括号多
return false;
}
}
return count === 0;
}
115. 不同的子序列 (hard)
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,“ACE” 是 “ABCDE” 的一个子序列,而 “AEC” 不是)
题目数据保证答案符合 32 位带符号整数范围。
示例 1:
输入:s = “rabbbit”, t = “rabbit”
输出:3
解释:
如下图所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
rabbbit
rabbbit
rabbbit
示例 2:输入:s = “babgbag”, t = “bag”
输出:5
解释:
如下图所示, 有 5 种可以从 s 中得到 “bag” 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag提示:
0 <= s.length, t.length <= 1000
s 和 t 由英文字母组成
方法1.动态规划
-
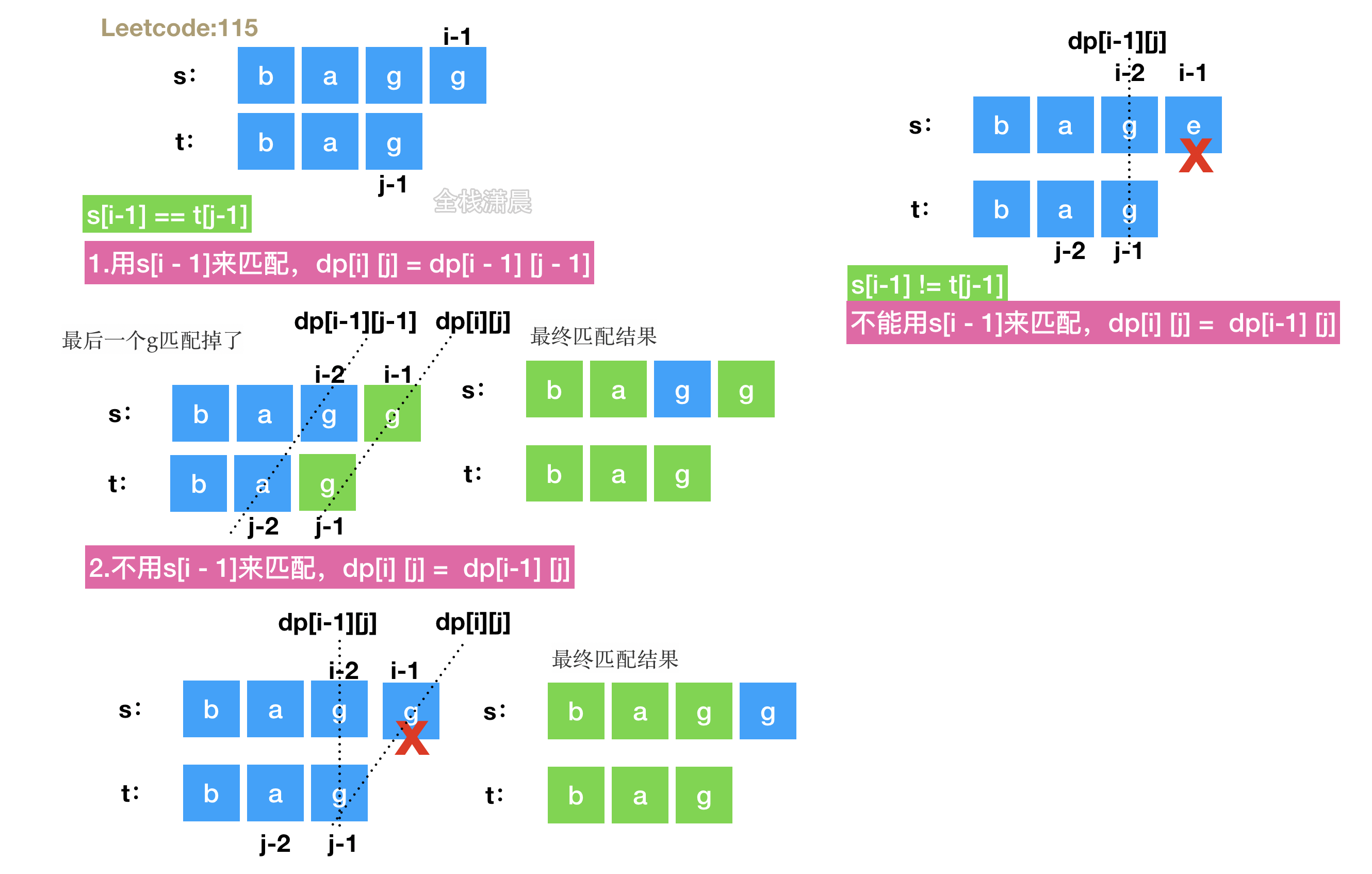
思路:拆分成不同子串的匹配,这些匹配存在重复子结构,可以用动态规划来做
-
状态定义:
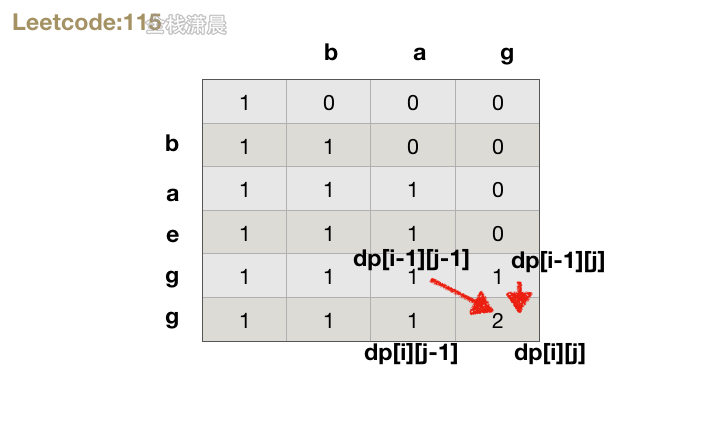
dp[i][j]表示以i-1为结尾的s,它的子序列中出现以j-1为结尾的t的个数为dp[i][j] -
状态转移方程:
-
s[i-1] == t[j-1]时:1.用
s[i - 1]来匹配,dp[i][j] = dp[i - 1][j - 1],2.不用
s[i - 1]来匹配,dp[i][j] = dp[i-1][j]。 -
s[i-1] != t[j-1]时:就不能用s[i - 1]来匹配,dp[i][j] = dp[i-1][j]
-
-
初始状态:
dp[i][0] =1:当j=0时,相当于t是空字符串,空字符在另一个字符串的子串中出现一次,此时第一列都初始化为1。- 其他情况:初始化的时候
dp[i][j] =0
-
-
复杂度:时间复杂度
O(mn),m,n分别是s和t的长度。空间复杂度O(mn),dp数组的空间
js:
//dp[i][j]表示以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
const numDistinct = (s, t) => {
//初始化dp数组,
let dp = Array.from(Array(s.length + 1), () => Array(t.length +1).fill(0));
//当j=0时,相当于t是空字符串,空字符在另一个字符串的子串中出现一次,此时第一列都初始化为1,
for(let i = 0; i <=s.length; i++) {
dp[i][0] = 1;
}
//当s[i-1] == t[j-1]:
//1.用s[i - 1]来匹配 dp[i][j] = dp[i-1][j-1]
//2.不用s[i - 1]来匹配 dp[i][j] = dp[i-1][j]
//当s[i-1] != t[j-1]:不能用s[i-1]来匹配,s[i - 1]匹配不了t[j-1],所以dp[i][j] = dp[i-1][j]
for(let i = 1; i <= s.length; i++) {
for(let j = 1; j<= t.length; j++) {
if(s[i-1] === t[j-1]) {
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
} else {
dp[i][j] = dp[i-1][j]
}
}
}
return dp[s.length][t.length];
};
557. 反转字符串中的单词 III (easy)
给定一个字符串 s ,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
示例 1:
输入:s = “Let’s take LeetCode contest”
输出:“s’teL ekat edoCteeL tsetnoc”
示例 2:输入: s = “God Ding”
输出:“doG gniD”提示:
1 <= s.length <= 5 * 104
s 包含可打印的 ASCII 字符。
s 不包含任何开头或结尾空格。
s 里 至少 有一个词。
s 中的所有单词都用一个空格隔开。
方法1:借助api
// "Let's take LeetCode contest"
const reverseWords = s => {
const arr = s.split(' ');
const res = [];
for (let i = 0; i < arr.length; i++) {
res.push(arr[i].split('').reverse().join(''));
}
return res.join(' ');
};
方法2:双指针
js:
// "Let's take LeetCode contest"
var reverseWords = function (s) {
let arr = s.split("");
let l = 0, r = l;
while (l < arr.length) {
//找到结尾的空格
while (arr[r] && arr[r] !== " ") {
r++;
}
//反转单词
for (let i = l, j = r - 1; i < j; i++, j--) {
[arr[i], arr[j]] = [arr[j], arr[i]];
}
//跳到下一个单词
l = r + 1;
r = l;
}
return arr.join("");
};
32. 最长有效括号 (hard)
给你一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = “(()”
输出:2
解释:最长有效括号子串是 “()”
示例 2:输入:s = “)()())”
输出:4
解释:最长有效括号子串是 “()()”
示例 3:输入:s = “”
输出:0提示:
0 <= s.length <= 3 * 104
s[i] 为 ‘(’ 或 ‘)’
方法1.动态规划
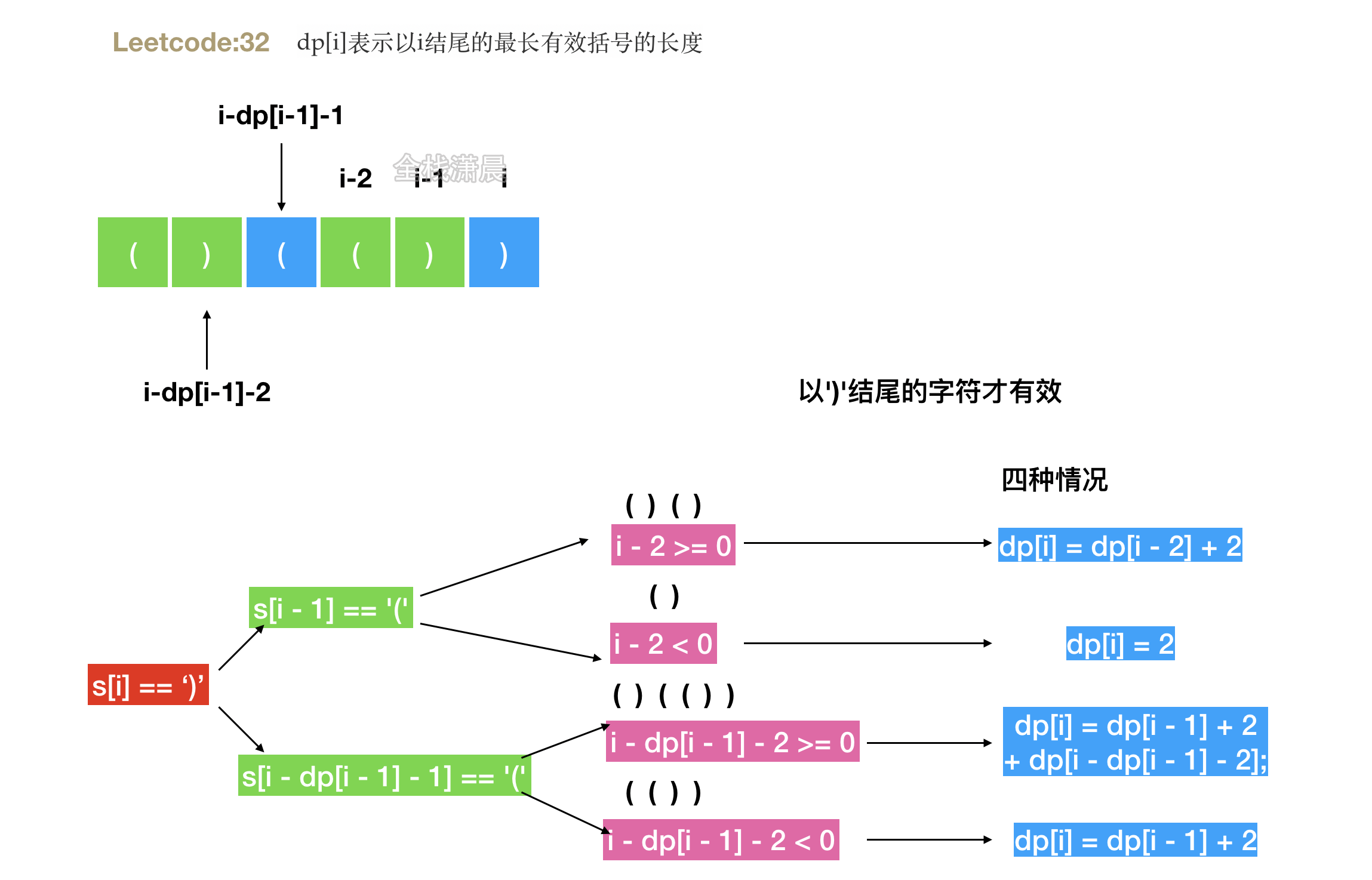
- 思路:
dp[i]表示以i结尾的最长有效括号的长度,分为4种情况,看图 - 复杂度:时间复杂度
O(n),n是字符串的长度,总共遍历1次。空间复杂度O(n),即dp数组的空间
js:
const longestValidParentheses = (s) => {
let maxLen = 0;
const len = s.length;
const dp = new Array(len).fill(0);
for (let i = 1; i < len; i++) {
if (s[i] == ')') {//以')'结尾的字符才有效
if (s[i - 1] == '(') {//如果前一个位置是'(' 则能与当前字符形成有效括号
if (i - 2 >= 0) {//如果前2个位置还有字符串
dp[i] = dp[i - 2] + 2;//当前状态等于 当前匹配的2个字符 加上 前两个位置匹配最长字符长度
} else {//如果前2个位置没有字符串
dp[i] = 2;//当前状态等于 当前匹配的2个字符
}
//以i-1结尾的有效字符在向前看1个位置 如果是'(' 则能与当前字符形成有效括号
} else if (s[i - dp[i - 1] - 1] == '(') {
if (i - dp[i - 1] - 2 >= 0) {//以i-1结尾的有效字符在向前看2个位置 如果>=于0
//当前状态=以i-1结尾的有效字符长度 + 当前匹配2个有效括号 + 以i - dp[i - 1] - 2结尾的有效字符长度
dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] - 2];
} else {
//以i-1结尾的有效字符在向前看2个位置 如果<于0
//当前状态=以i-1结尾的有效字符长度 + 当前匹配2个有效括号
dp[i] = dp[i - 1] + 2;
}
}
}
maxLen = Math.max(maxLen, dp[i]);
}
return maxLen;
};
方法2.栈
- 思路:遍历字符串,准备一个栈,存放字符串下标,首先放入初始参照物-1,遇到’(‘入栈,遇到’)'出栈,并且判断栈长度,如果不为空,更新最大合法字符串长度,否则将当前下标放入栈中
- 复杂度:时间复杂度
O(n),n是字符串的长度,总共遍历1次。空间复杂度O(n),即栈的空间
动画过大,点击查看
js:
var longestValidParentheses = function (s) {
let maxLen = 0
let stack = []
stack.push(-1) // 初始化一个参照物
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {
// ( 入栈 )出栈
stack.push(i)
} else {
// )的情况 出栈
stack.pop()
if (stack.length) {
// 每次出栈 计算下当前有效连续长度
// 如何计算连续长度 当前位置 - 栈顶下标
maxLen = Math.maxLen(maxLen, i - stack[stack.length - 1])
} else {
stack.push(i) //栈为空时 放入右括号参照物 表示从这个下标开始 需要重新计算长度
}
}
}
return maxLen
};
方法3.两次遍历
- 思路:从左到右,从右到左依次遍历字符串,遇见’(’ ,
left++,遇见’)’ ,right++,当左右括号数量相同时,更新最大长度,如果right大于left,则重置left、right 重新计数 - 复杂度:时间复杂度
O(n),n是字符串的长度,总共遍历2次。空间复杂度O(1)

Js:
var longestValidParentheses = function (s) {
let maxLen = 0;
let left = 0;
let right = 0;
for (let i = 0; i < s.length; i++) {//从左往右
if (s[i] == "(") { //遇见'(' left++
left++;
} else {
right++; //遇见')' right++
}
if (left == right) { //左右数量相同
maxLen = Math.max(maxLen, 2 * left); //更新最大长度
} else if (right > left) { //right大于left 重置left right 重新计数
left = right = 0;
}
}
left = right = 0;
for (let i = s.length - 1; i >= 0; i--) { //从右往左
if (s[i] == "(") {
left++;
} else {
right++;
}
if (left == right) {
maxLen = Math.max(maxLen, right * 2);
} else if (left > right) {
left = right = 0;
}
}
return maxLen;
};
14. 最长公共前缀 (easy)
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 “”。
示例 1:
输入:strs = [“flower”,“flow”,“flight”]
输出:“fl”
示例 2:输入:strs = [“dog”,“racecar”,“car”]
输出:“”
解释:输入不存在公共前缀。提示:
1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 仅由小写英文字母组成
- 思路:纵向扫描字符串,找到第一个不相同的位置
- 复杂度:时间复杂度
O(mn),m是字符串最长长度,n是字符数组长度
f l o w e r
f l o w
f l i g h t
js:
var longestCommonPrefix = function(strs) {
if(strs.length == 0)
return "";
let ans = strs[0];//ans初始值为字符串数组的第一个
for(let i =1;i<strs.length;i++) {//循环字符串数组
let j=0;
for(;j<ans.length && j < strs[i].length;j++) {//循环字符,找到第一个不相同的位置
if(ans[j] != strs[i][j])
break;
}
ans = ans.substr(0, j);//从0号位置到第一个不相同的位置 截取字符串
if(ans === "")
return ans;
}
return ans;
};
680. 验证回文字符串 Ⅱ (easy)
给你一个字符串 s,最多 可以从中删除一个字符。
请你判断 s 是否能成为回文字符串:如果能,返回 true ;否则,返回 false 。
示例 1:
输入:s = “aba”
输出:true
示例 2:输入:s = “abca”
输出:true
解释:你可以删除字符 ‘c’ 。
示例 3:输入:s = “abc”
输出:false提示:
1 <= s.length <= 105
s 由小写英文字母组成
- 思路:对撞指针不断判断左右两边的数字是否相等 ,如果不相等还有一次机会,左指针向前一步或者右指针向后一步继续验证
- 复杂度:时间复杂度
O(n),空间复杂度O(1)。
例子:
输入: s = "aba"
输出: true
输入: s = "abca"
输出: true
解释: 你可以删除c字符。
js:
function isPalindrome(str, l, r) {
while (l < r) { //对撞指针不断判断两边的数字是否相等
if (str[l] != str[r]) {
return false;
}
l++;
r--;
}
return true;
}
var validPalindrome = function (str) {
let l = 0, r = str.length - 1; //头尾指针
while (l < r) {
if (str[l] != str[r]) {//左右指针不一样 还有一次机会,左指针向前一步或者右指针向后一步继续验证
return isPalindrome(str, l + 1, r) || isPalindrome(str, l, r - 1);
}
l++;
r--;
}
return true;
};
5. 最长回文子串 (medium)
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = “babad”
输出:“bab”
解释:“aba” 同样是符合题意的答案。
示例 2:输入:s = “cbbd”
输出:“bb”提示:
1 <= s.length <= 1000
s 仅由数字和英文字母组成
方法1.动态规划
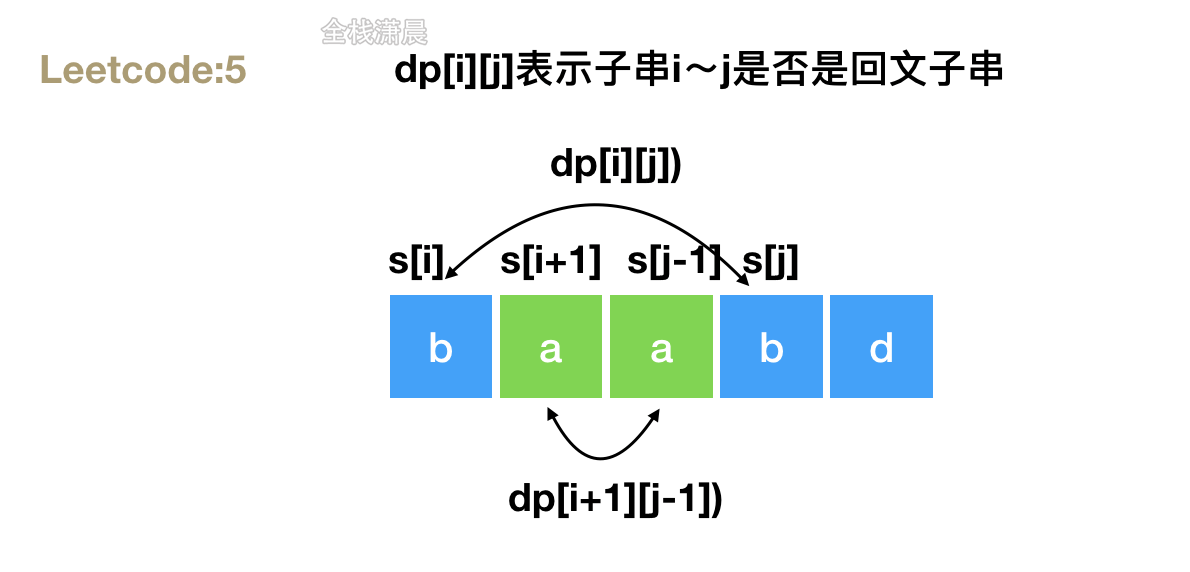
- 思路:定义
dp[i][j]表示子串i~j是否是回文子串,循环s的子串,看是否满足s[i],s[j]相等,如果相等,则dp[i][j]是否为回文串取决于dp[i+1][j-1]是否也是回文子串,在循环的过程中不断更新最大回文子串的长度,注意子串的长度是0或1也算回文子串 - 复杂度:时间复杂度
O(n^2),两层循环。空间复杂度O(n^2),即动态规划dp数组的空间。
Js:
var longestPalindrome = function(s) {
let n = s.length;
let res = '';
let dp = Array.from(new Array(n),() => new Array(n).fill(false));//初始化数组
for(let i = n-1;i >= 0;i--){//循环字符串
for(let j = i;j < n;j++){
//dp[i][j]表示子串i~j是否是回文子串
//回文子串必须满足s[i],s[j]相等。并且向外扩展一个字符也相等,即dp[i+1][j-1]也是回文子串
//j - i < 2表示子串小于等于1也是回文串
dp[i][j] = s[i] == s[j] && (j - i < 2 || dp[i+1][j-1]);
if(dp[i][j] && j - i +1 > res.length){//当前回文子串比之前的大,更新最大长度
res = s.substring(i,j+1);
}
}
}
return res;
};
方法2.中心扩散法
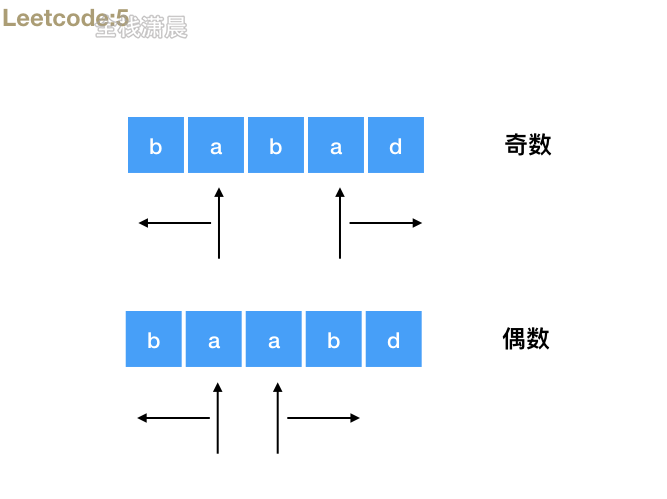
- 思路:分最长回文子串是奇数和偶数的情况,定义start为最长回文子串开始的索引,然后循环字符串,不断不断向外扩展回文字符串的长度,循环的过程中更新最大回文子串的长度和start的位置,最后返回start到
start+ maxLength的子串就是本题的答案 - 复杂度:时间复杂度
O(n^2),循环字符串一次,每次循环内部又向外不断扩张。空间复杂度O(1)
Js:
var longestPalindrome = function (s) {
if (s.length <= 0) {//边界条件
return s;
}
let start = 0;//最长回文子串开始的索引
let maxLength = 1;//初始化最大回文子串长度
function h(left, right) {
//当s[left],和 s[right]想等时,不断向外扩展回文字符串的长度
while (left >= 0 && right < s.length && s[left] === s[right]) {
if (right - left + 1 > maxLength) {
maxLength = right - left + 1;//更新最大回文子串的长度
start = left;//更新start的位置
}
left--;
right++;
}
}
for (let i = 0; i < s.length; i++) {
h(i - 1, i + 1);//回文子串是奇数
h(i, i + 1);//回文子串是偶数
}
return s.substring(start, start + maxLength);
};
151. 翻转字符串里的单词 (medium)
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。示例 1:
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]输出:
[null,null,null,null,-3,null,0,-2]解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.提示:
-231 <= val <= 231 - 1
pop、top 和 getMin 操作总是在 非空栈 上调用
push, pop, top, and getMin最多被调用 3 * 104 次
方法1:正则
- 思路:将字符串头尾空格去掉,然后将那个多个空格用正则替换成一个空格,根据空格分隔成数组,然后翻转转回字符串
js:
var reverseWords = function(s) {
return s.trim().replace(/\s+/g, ' ').split(' ').reverse().join(' ')
};
方法2:双端队列
- 思路:left指针初始在0号位置,right指针初始在
s.length - 1位置,遍历字符串,将每个由空格分隔的字符串加入队列,最后在转回字符串就是翻转过后的了 - 复杂度:时间复杂度
O(n),空间复杂度O(n)
js:
//"the sky is blue"
var reverseWords = function(s) {
let left = 0
let right = s.length - 1
let queue = []
let word = ''
//去掉左右的空格
while (s.charAt(left) === ' ') left ++
while (s.charAt(right) === ' ') right --
while (left <= right) {
let char = s.charAt(left)
if (char === ' ' && word) {
queue.unshift(word)//字符串加入队列
word = ''//重置字符串
} else if (char !== ' '){//拼接单个字符串
word += char
}
left++
}
queue.unshift(word)//最后一个字符串也要加入队列
return queue.join(' ')//转回字符串
};
视频讲解:传送门





![[ins 2022] 针对已见和未见群体的群体推荐中的贝叶斯归纳学习](https://img-blog.csdnimg.cn/img_convert/cb39c564d59d5b69d21660db8aadd50a.jpeg)