基于Bayes_opt实现GP优化
bayes-optimization是最早开源的贝叶斯优化库之一,也是为数不多至今依然保留着高斯过程优化的优化库。由于开源较早、代码简单,bayes-opt常常出现在论文、竞赛kernels或网络学习材料当中,因此理解Bayes_opt的代码是极其重要的课题。不过,bayes-opt对参数空间的处理方式较为原始,也缺乏相应的提效/监控功能,对算力的要求较高,因此它往往不是我们进行优化时的第一首选库。通常来说,当且仅当我们必须要实现基于高斯过程的贝叶斯优化,且算法的参数空间中带有大量连续型参数时,我们才会优先考虑Bayes_opt库。
pip install bayesian-optimization #安装Bayes_opt库
pip install hyperopt #安装Hyperopt库
import numpy as np
import pandas as pd
import time
#算法/损失/评估指标等
import sklearn
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import KFold, cross_validate
#优化器
from bayes_opt import BayesianOptimization
import hyperopt
from hyperopt import hp, fmin, tpe, Trials, partial
生成数据集
import numpy as np
from sklearn.datasets import make_regression
# Generate a regression dataset
X, y = make_regression(n_samples=1000, n_features=10, random_state=1412)
1 定义目标函数
目标函数的值即𝑓(𝑥)的值。贝叶斯优化会计算𝑓(𝑥)在不同𝑥上的观测值,因此𝑓(𝑥)的计算方式需要被明确。在HPO过程中,我们希望能够筛选出令模型泛化能力最大的参数组合,因此𝑓(𝑥)应该是损失函数的交叉验证值或者某种评估指标的交叉验证值。
Notes:
-
在定义目标函数时,我们需要确保超参数作为输入,而不是整个超参数空间或其他元素,例如数据或算法超参数。因此,目标函数的输入必须是具体的超参数值。
-
当需要对算法的实际参数进行调整时,需要注意超参数的输入值只能是浮点数,不支持整数或字符串。如果算法参数需要是字符串,则无法使用bayes_opt进行调整;如果参数需要是整数,则需要在目标函数中规定参数的类型。
-
bayes_opt只能寻找𝑓(𝑥)的最大值,而不能寻找最小值。因此,当目标函数代表某种损失时,输出需要取负值。例如,如果使用RMSE作为目标函数,则应该让目标函数输出负的RMSE,以便最大化负的RMSE,从而实现最小化真正的RMSE。对于准确率、AUC等指标作为目标函数的情况,则可以保持输出值不变。
def bayesopt_objective(n_estimators,max_depth,max_features,min_impurity_decrease):
#定义评估器
#需要调整的超参数等于目标函数的输入,不需要调整的超参数则直接等于固定值
#默认参数输入一定是浮点数,因此需要套上int函数处理成整数
reg = RFR(n_estimators = int(n_estimators)
,max_depth = int(max_depth)
,max_features = int(max_features)
,min_impurity_decrease = min_impurity_decrease
,random_state=1412
,verbose=False #可自行决定是否开启森林建树的verbose
,n_jobs=-1)
#定义损失的输出,5折交叉验证下的结果,输出负根均方误差(-RMSE)
#注意,交叉验证需要使用数据,但我们不能让数据X,y成为目标函数的输入
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
validation_loss = cross_validate(reg,X,y
,scoring="neg_root_mean_squared_error"
,cv=cv
,verbose=False
,n_jobs=-1
,error_score='raise'
#如果交叉验证中的算法执行报错,则告诉我们错误的理由
)
#交叉验证输出的评估指标是负根均方误差,因此本来就是负的损失
#目标函数可直接输出该损失的均值
return np.mean(validation_loss["test_score"])
2 定义参数空间
在bayes_opt中,我们使用字典方式来定义参数空间,其中参数的名称为键,参数的取值范围为值。且任意参数的取值范围为双向闭区间,以下方的空间为例,在n_estimators的取值中,80与100都可以被取到。
Notes:
- bayes_opt只支持填写参数空间的上界与下界,不支持填写步长等参数;
- bayes_opt会将所有参数都当作连续型超参进行处理,因此bayes_opt会直接取出闭区间中任意浮点数作为备选参数。例如,取92.28作为n_estimators的值;
- 输入bayes_opt的参数空间天生会比其他贝叶斯优化库更大/更密,因此需要的迭代次数也更多。
param_grid_simple = {'n_estimators': (80,100)
, 'max_depth':(10,25)
, "max_features": (10,20)
, "min_impurity_decrease":(0,1)
}
3 定义优化目标函数的具体流程
-
一旦我们确定了目标函数和参数空间,就可以按照bayes_opt的规则进行优化了。在任何贝叶斯优化算法的实践过程中,都会涉及到一定程度的随机性,比如随机抽取点作为观测点,随机抽样部分观测点进行采集函数的计算等。在大多数优化库中,这种随机性是无法被控制的,即使允许我们填写随机数种子,优化算法也无法被固定下来。因此,尽管我们可以尝试填写随机数种子,但需要记住每次运行优化算法时都会产生不同的结果。
-
尽管优化算法无法被精确复现,但是得出的最佳超参数结果却是可以被复现的。一旦优化完成,可以从优化算法的实例化对象中获取最佳参数组合和最佳分数,然后将最佳参数组合输入到交叉验证中,这样一定可以复现其最佳分数。如果未能复现最佳分数,那么可能是由于交叉验证过程中的随机数种子设置存在问题,或者优化算法的迭代流程存在问题。
def param_bayes_opt(init_points,n_iter):
#定义优化器,先实例化优化器
opt = BayesianOptimization(bayesopt_objective #需要优化的目标函数
,param_grid_simple #备选参数空间
,random_state=1412 #随机数种子,虽然无法控制住
)
#使用优化器,记住bayes_opt只支持最大化
opt.maximize(init_points = init_points #抽取多少个初始观测值
, n_iter=n_iter #一共观测/迭代多少次
)
#优化完成,取出最佳参数与最佳分数
params_best = opt.max["params"]
score_best = opt.max["target"]
#打印最佳参数与最佳分数
print("\n","\n","best params: ", params_best,
"\n","\n","best cvscore: ", score_best)
#返回最佳参数与最佳分数
return params_best, score_best
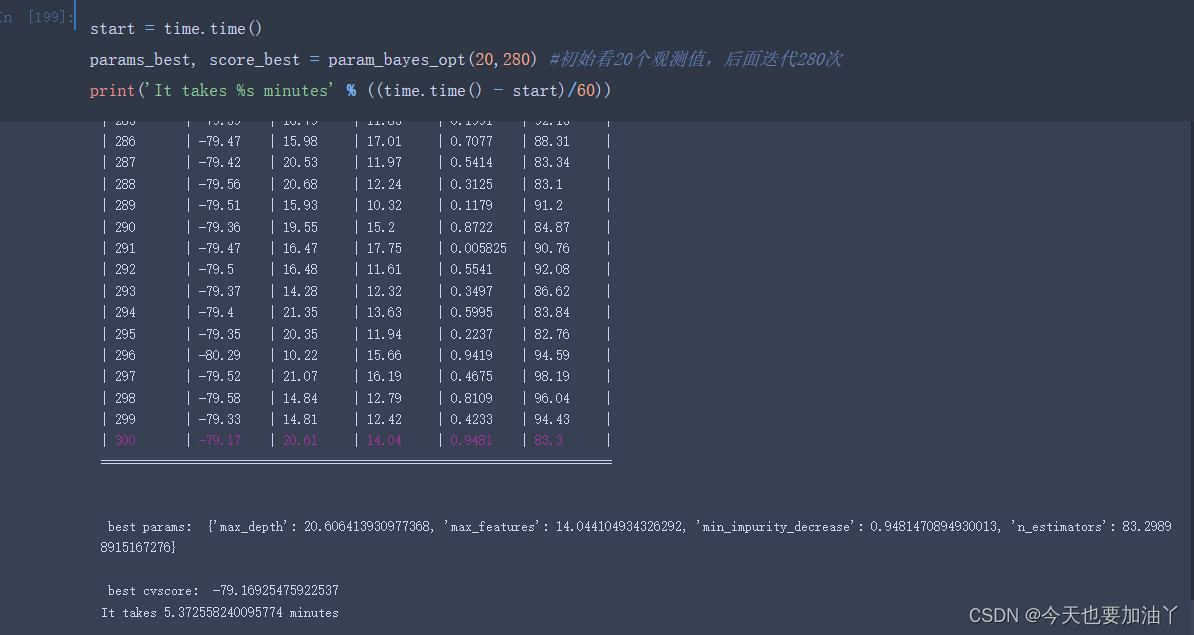
5 执行实际优化流程