格密码基础：最短格基与KZ基

news2024/10/3 0:28:20

一. 介绍

二. 最短向量长度

三. GapSVP问题的困难性

四. 如何解决近似SVP问题

五. 推荐论文

一. 介绍

KZ基的全称叫Korkine-Zolotarev格基，KZ基也被称之为最短的格基。接下来我们介绍什么是KZ基？

给定任意秩为n的格 $\Lambda$ ，首先第一步寻找其最短的向量，记作 $b_1$ ，这个就是KZ基的第一个向量。

格的扩展空间写做：

$span(\Lambda)$

将此扩展空间垂直投影于向量 $b_1$ ，形成一个子空间（subspace）。接着将格点 $\Lambda$ 投影于此子空间形成新的格点叫做 $\Lambda'$ ，将此新的格中最短的格向量叫做 $c_2$ 。以上过程可直接抽象看成：

接着寻找满足如下等式的向量：

$b_i=c_i+\alpha_ib_1$

其中 $\alpha$ 的取值如下：

$\alpha_i\in(-\frac{1}{2},\frac{1}{2})$

由此就可以确定原来的格的第二个格基 $b_2$ 。根据以上讨论我们发现 $\Lambda'$ 的KZ基即为：

$c_2,\cdots,c_n$

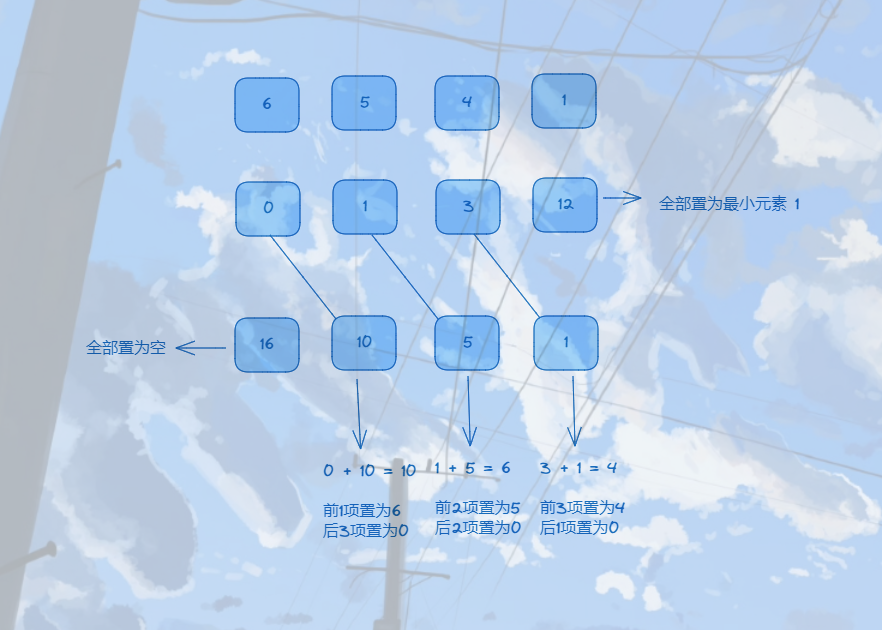
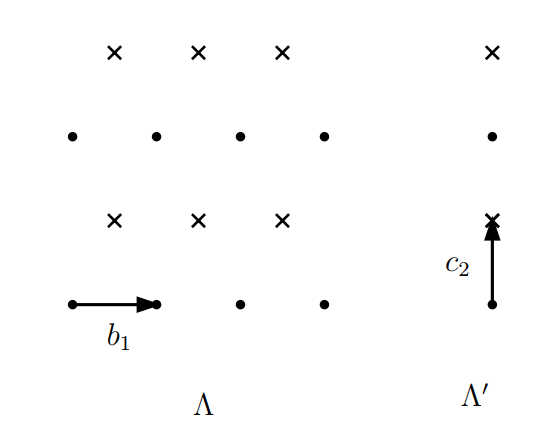
利用迭代的思想便可以找到满足的n个格点，从这n个格点放在一起便形成了我们想要的KZ基，如下图：

二. 最短向量长度

以上讨论中的 $\Lambda'$ 也是一个格， $b_1$ 是此格中最短的向量，所以肯定是一个格内的一个本原向量，简单解释就是其整数倍系数组合时最大公约数为1.KZ基的本质就是一组格基，那它有啥用呢？

接下来我们将介绍由Lagarias, Lenstra 和 Schnorr发现的一个有关最短格向量长度的一个定理。在格密码专栏中，我们已经介绍过了最短向量有一个下界，是用格基正交化的结论来衡量的，也就是：

$min(||\tilde b_1||,\cdots,||\tilde b_n||)\leq \lambda_1(\Lambda)$

同样的形式，我们今天来看一个很类似的结论：

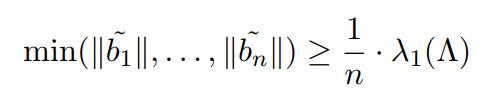
两个结论写在一起便构成了最短格向量长度的上界与下界。

证明：

假定对偶格 $\Lambda^*$ 的KZ基如下：

$d_1,\cdots,d_n$

其对应的原格基为：

$b_n,\cdots,b_1$

注意是逆序的。

对偶格基与原格基正交化后满足如下结论：

$\tilde b_i=\frac{\tilde d_i}{||d_i||^2}$

此时原定理相当于要证明：

$min(||\tilde d_1||,\cdots,||\tilde d_n||)\leq \frac{n}{\lambda_1(\Lambda)}$

备注：此处就是利用对偶格基向量长度为倒数

根据KZ基的定义， $\tilde d_1$ 是对偶格 $\Lambda^*$ 中最短的向量，由此易得：

$||\tilde d_1||\leq \frac{n}{\lambda_1(\Lambda)}$

根据格基正交化理论，可得：

$\tilde d_2=\pi_2(d_2)$

该向量即为如下格的最短向量：

$L(\pi_2(d_2),\cdots,\pi_2(d_n))$

易得该格的对偶格即为：

$L(b_2,\cdots,b_n)$

很容易得该格是原来格 $\Lambda$ 的子格，所以可得：

$\lambda_1(L(b_2,\cdots,b_n))\geq \lambda_1(\Lambda)$

由此可得：

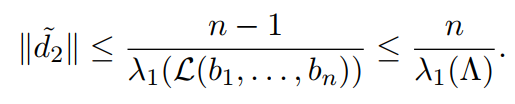
以上我们利用迭代的性质证明了第1维和第2维符合定理，继续类推容易证明剩下的结论。

三. GapSVP问题的困难性

当近似因子为n时，GapSVP问题的输入为(B,d)，输出包含两种情况。

情况1 Yes instance：

$\lambda_1(L(B))\leq d$

情况2 No instance:

$\lambda_1(L(B))\geq nd$

定理 $GapSVP_n\in coNP$

证明：

GapSVP问题的答案，通常我们叫witness是n个格向量，如下：

$v_1,\cdots,v_n$

该n个格向量需要组成格基L(B)，并且如果满足如下：

$min(||\tilde v_1||,\cdots,||\tilde v_n||)> d$

此时GapSVP会输出No

证明如下：

如果最短格向量满足：

$\lambda_1(L(B))\geq nd$

那么上面定理中一定能找到这样的一组格基。

如果最短格向量满足：

$\lambda_1(L(B))\leq d$

那么可运算得：

此时则找不到对应的witness

此时证明完毕，近似GapSVP问题是CoNP类。

其实可以类推，当近似因子为 $\sqrt n$ 时，GapCVP和GapSVP均为CoNP类。

四. 如何解决近似SVP问题

格密码专栏已经介绍过Minkowski定理，对任意的最短格向量的长度，均满足：

$\lambda_1(\Lambda)\leq \sqrt n(det(\Lambda))^{\frac{1}{n}}$

在很多网络安全的应用时，我们需要进一步缩小这个界限。如果我们能找到一个格向量的长度为 $\sqrt n(det(\Lambda))^{\frac{1}{n}}$ ，那么我们就可以解决近似因子为n的SVP问题，来看一个定理：

定理：

给定一个格基B，如果存在一个算法A能找到一个非零的格向量，也就是:

$v\in L(B)$

该格向量的长度满足：

$||v||\leq f(n)\cdot(det(L(B)))^{\frac{1}{n}}$

其中f(n)要求不是递减函数，那么借助该算法我们就可以解决近似因子为 $(f(n))^2$ 的SVP问题。

证明：

对格L(B)和对偶格 $L(B)^*$ 分别运用算法A，可得：

$u\in L(B)\quad v\in L(B)^*$

使其满足：

$||u||\leq f(n)\cdot(det(L(B)))^{\frac{1}{n}}$

$||v||\leq f(n)\cdot(det(L(B)))^{-\frac{1}{n}}$

两者长度相乘可得：

$||u||||v||\leq (f(n))^2$

接下来的证明需要再利用一个推论。

先来看该定理形式化的表达：

证明：

证明的主题思想是迭代法（recursive）与KZ基。

对于任意给定的格，输出格 $\Lambda$ 中的n个非零向量：

$u_1,\cdots,u_n$

输出对偶格 $\Lambda^*$ 中的一个格基：

$v_1,\cdots,v_n$

具体过程如下：

根据如上算法A，先获得格向量 $u_1$ ，接下来获得格向量 $v_1$ ，将其表示成：

$v_1=\sum a_ib_i$

如果发现其系数的最大公因子不为1的话，则运算：

$v_1/gcd(a_1,\cdots,a_n)$

由此便可以得到本原格向量 $v_1$

将对偶格点垂直投影于向量 $v_1$ ，将新的格记为 $\Lambda'$ 。然后迭代操作，使其满足：

$v_i=v_i'+\alpha_iv_i$

其中：

$\alpha_i\in(-\frac{1}{2},\frac{1}{2})$

不要忘记 $v_i\in \Lambda^*$ 。由此不断迭代操作，便可以获得：

$u_2,\cdots,u_n\quad v_2,\cdots,v_n$

根据以上运算过程，对偶格 $\Lambda^*$ 的格基既是：

$v_1,\cdots,v_n$

并且每轮迭代时，都满足函数关系：

$||u_i||||v_i||\leq g(n-i+1)\leq g(n)$

根据对偶格的性质，可得如下：

换种表达的形式可得：

根据以上便可以解决近似因子为g(n)的SVP问题。

五. 推荐论文

（1）解释格困难问题的NP与coNP

D. Aharonov and O. Regev. Lattice problems in NP intersect coNP. In Proc. 45th Annual IEEE Symp. on Foundations of Computer Science (FOCS), pages 362–371, 2004.

（2）解释KZ基与最短格基

J. C. Lagarias, H. W. Lenstra, Jr., and C.-P. Schnorr. Korkin-Zolotarev bases and successive minima of a lattice and its reciprocal lattice. Combinatorica, 10(4):333–348, 1990.

（3）更高端的BKZ 2.0算法

Y. Chen, P.Q. Nguyen, BKZ 2.0: Better lattice security estimates. AdvancesinCryptology– ASIACRYPT 2011, Lecture Notes in Computer Science, vol. 7073(Springer,Berlin, 2011), pp.1–20

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1394931.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！