说在前面
🎈不知道大家对于算法的学习是一个怎样的心态呢?为了面试还是因为兴趣?不管是出于什么原因,算法学习需要持续保持。
题目描述
请你从每个袋子中 拿出 一些豆子(也可以 不拿出),使得剩下的 非空 袋子中(即 至少还有一颗 魔法豆的袋子)魔法豆的数目 相等。一旦把魔法豆从袋子中取出,你不能再将它放到任何袋子中。
请返回你需要拿出魔法豆的 最少数目。
示例 1:
输入:beans = [4,1,6,5]
输出:4
解释:
- 我们从有 1 个魔法豆的袋子中拿出 1 颗魔法豆。
剩下袋子中魔法豆的数目为:[4,0,6,5]
- 然后我们从有 6 个魔法豆的袋子中拿出 2 个魔法豆。
剩下袋子中魔法豆的数目为:[4,0,4,5]
- 然后我们从有 5 个魔法豆的袋子中拿出 1 个魔法豆。
剩下袋子中魔法豆的数目为:[4,0,4,4]
总共拿出了 1 + 2 + 1 = 4 个魔法豆,剩下非空袋子中魔法豆的数目相等。
没有比取出 4 个魔法豆更少的方案。
示例 2:
输入:beans = [2,10,3,2]
输出:7
解释:
- 我们从有 2 个魔法豆的其中一个袋子中拿出 2 个魔法豆。
剩下袋子中魔法豆的数目为:[0,10,3,2]
- 然后我们从另一个有 2 个魔法豆的袋子中拿出 2 个魔法豆。
剩下袋子中魔法豆的数目为:[0,10,3,0]
- 然后我们从有 3 个魔法豆的袋子中拿出 3 个魔法豆。
剩下袋子中魔法豆的数目为:[0,10,0,0]
总共拿出了 2 + 2 + 3 = 7 个魔法豆,剩下非空袋子中魔法豆的数目相等。
没有比取出 7 个魔法豆更少的方案。
提示:
- 1 <= beans.length <= 105
- 1 <= beans[i] <= 105
解题思路
这道题我们比较容易看出其实就是一道前缀和的题目,我们可以分为以下几步来进行解题,这里我们以示例一为例子来详说解题步骤:
对数组进行排序
我们可以先对数组进行排序
beans.sort((a, b) => b - a);
排序后的数组如下:

计算每个下标前面的元素置为当前元素值所需要减去的总和

[6] => [6] = 6 - 6 = 0
[6,5] => [5,5] = (6 - 5) + (5 - 5) = 1
[6,5,4] => [4,4,4] = (6 - 4) + (5 - 4) + (4 - 4) = 3
[6,5,4,1] => [1,1,1,1] = (6 - 1) + (5 - 1) + (4 - 1) + (1 - 1) = 12
从后往前计算前缀和

遍历每种取法,找出最小的取法
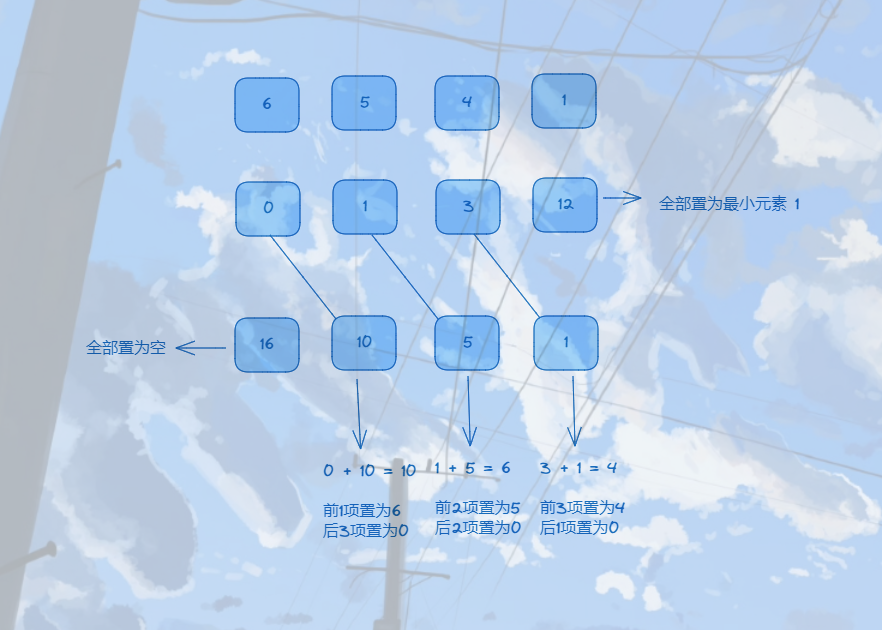
从上图我们可以看出前三项置为4,最后一下置为0是最优的取法。
AC代码
/**
* @param {number[]} beans
* @return {number}
*/
var minimumRemoval = function (beans) {
beans.sort((a, b) => b - a);
const cnt = new Array(beans.length).fill(0);
for (let i = 1; i < beans.length; i++) {
cnt[i] = (beans[i - 1] - beans[i]) * i + cnt[i - 1];
}
let min = cnt[cnt.length - 1];
let sum = 0;
for (let i = beans.length - 1; i > 0; i--) {
sum += beans[i];
min = Math.min(sum + cnt[i - 1], min);
}
return min;
};
公众号
关注公众号『前端也能这么有趣』,获取更多有趣内容。
说在后面
🎉 这里是 JYeontu,现在是一名前端工程师,有空会刷刷算法题,平时喜欢打羽毛球 🏸 ,平时也喜欢写些东西,既为自己记录 📋,也希望可以对大家有那么一丢丢的帮助,写的不好望多多谅解 🙇,写错的地方望指出,定会认真改进 😊,偶尔也会在自己的公众号『
前端也能这么有趣』发一些比较有趣的文章,有兴趣的也可以关注下。在此谢谢大家的支持,我们下文再见 🙌。