数据结构精讲——排序(二)
排序的分类
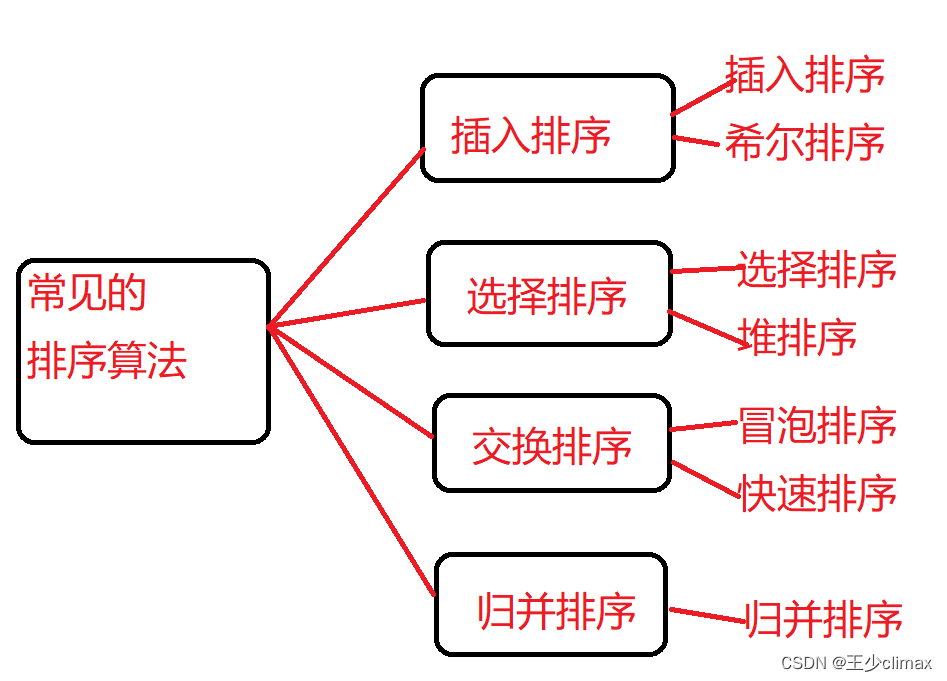
上节课我们已经了解过插入排序和选择排序,这节课主要讲的是快排排序,冒泡排序应该都很熟悉,少提一下吧。
冒泡排序
冒泡排序是我们刚接触编程时就学习的排序方法(还有选择排序)。
其原理就是将相邻的两个数据节点节进行比较然后慢慢完后转移比较,很像水中的泡泡。
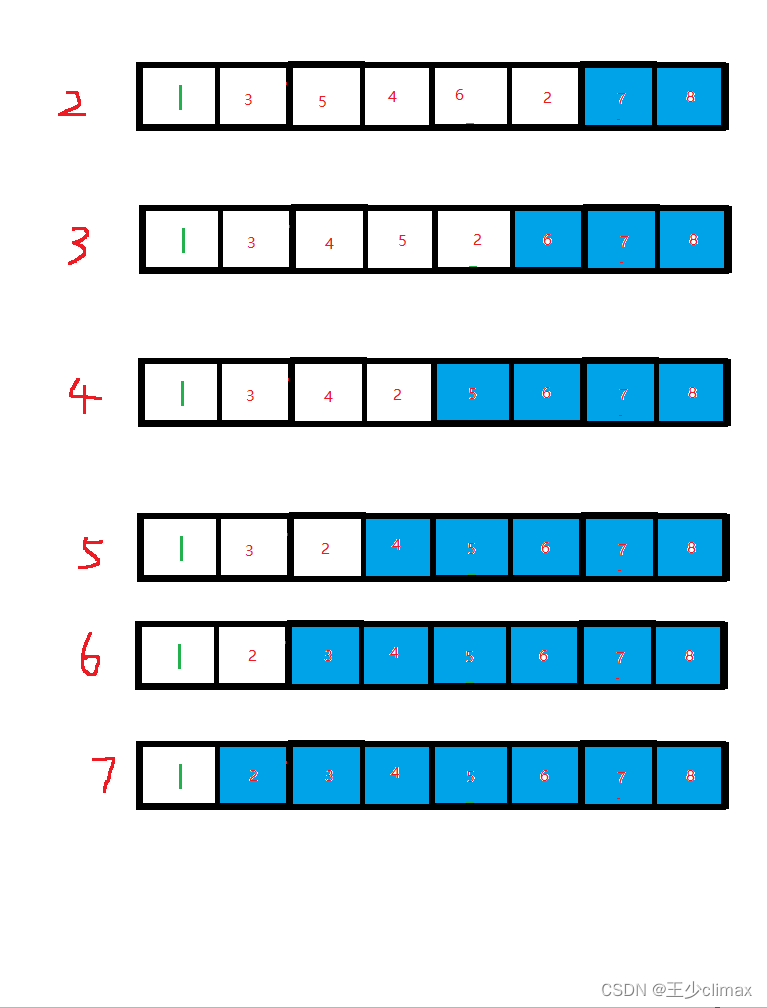
一共七趟(n-1趟)。
程序实现
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int a[] = { 1,8,7,3,5,4,6,2 };
int n = sizeof(a) / sizeof(a[0]);
for (int i = 0; i < n; i++)
{
for (int j = 1; j < n - i; j++)
{
if (a[j - 1] > a[j])
{
swap(a[j - 1], a[j]);
}
}
}
for (int i = 0; i < n; i++)
{
cout << a[i] <<' ';
}
return 0;
}
时间复杂度为O(n^2),所以效率并不高,但是好理解所以新手好学一下。
只是简单说一下,并不做重点。
快排
在学C语言时我们了解过qsort这个函数,其内核就是快排。

base是数组的第一个节点的指针,num是排序数组的成员个数(要排序几个成员),size是每一个成员的类型大小(char=1;double=8;int=4),compar是比较函数(需要在运算后将void*改成int返回出来)。
compare函数:

如果小于返回-1,如果大于返回1,等于返回0。
快排原理
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中
的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右
子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
if(right - left <= 1)
return;
// 按照基准值对array数组的 [left, right)区间中的元素进行划分
int div = partion(array, left, right);
// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
// 递归排[left, div),左闭右开
QuickSort(array, left, div);
// 递归排[div+1, right)
QuickSort(array, div+1, right);
}
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉
树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
将区间按照基准值划分为左右两半部分的常见方式有:
hoare版本
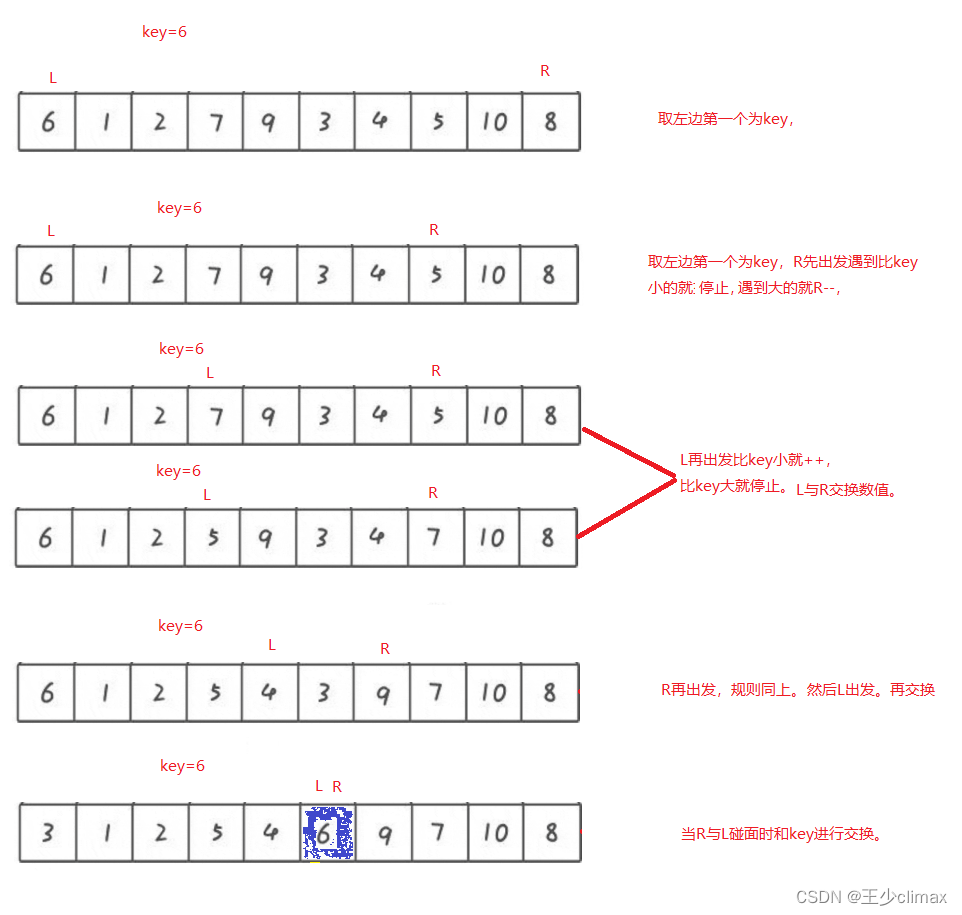
我们可以把L与R相遇的地方变成新keyi,新keyi左边都比keyi小,右边都比keyi大。
然后再进行递归。
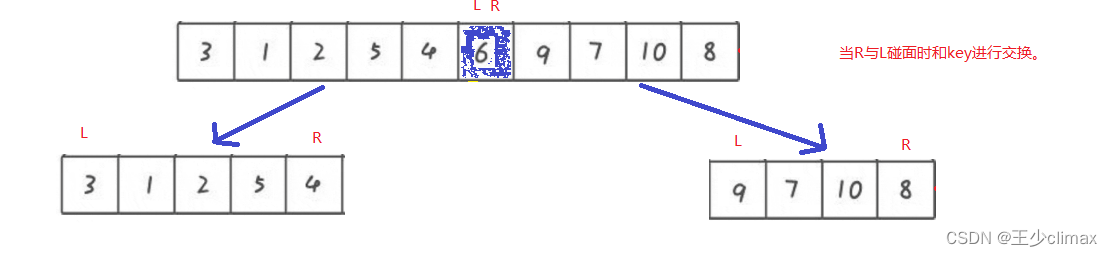
再进行分批排序。
void QSort1(int* a, int begin, int end)//hoare
{
int keyi = begin;
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] >= a[keyi])//右边找小于a[keyi]的数
{
right--;
}
while (left < right && a[left] <= a[keyi])//左边找大于a[keyi]的数
{
left++;
}
Swap(&a[left], &a[right]);
}
//将a[keyi]与相遇点交换(要保证相遇点比a[keyi]小,需要让right先走)
Swap(&a[keyi], &a[right]);
QSort1(a, begin, keyi-1);
QSort1(a, keyi+1,end);
}
挖坑法
先保存a[keyi]的值到int temp上,然后将keyi先作坑,int left=0、int right=n-1
先让right走,找到小于a[keyi]的数,就将它放在a[hole]处,更新hole=right。然后left再走,找到大于a[keyi]的数,然后将它放在a[hole]处,再次更新hole=left,再让right移动,left移动,直到left等于right。此时相遇点必然是一个坑,最后将temp放在a[hole]处。

int Q_PartSort2(int* a, int begin, int end)//挖坑法
{
int key = a[begin];
int hole = begin;
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
void _QuickSort(int* a, int begin, int end)//递归
{
if (begin >= end)
{
return;
}
int keyi = Q_PartSort2(a, begin, end);
_QuickSort(a, begin, keyi - 1);
_QuickSort(a, keyi + 1, end);
}
前后指针版本
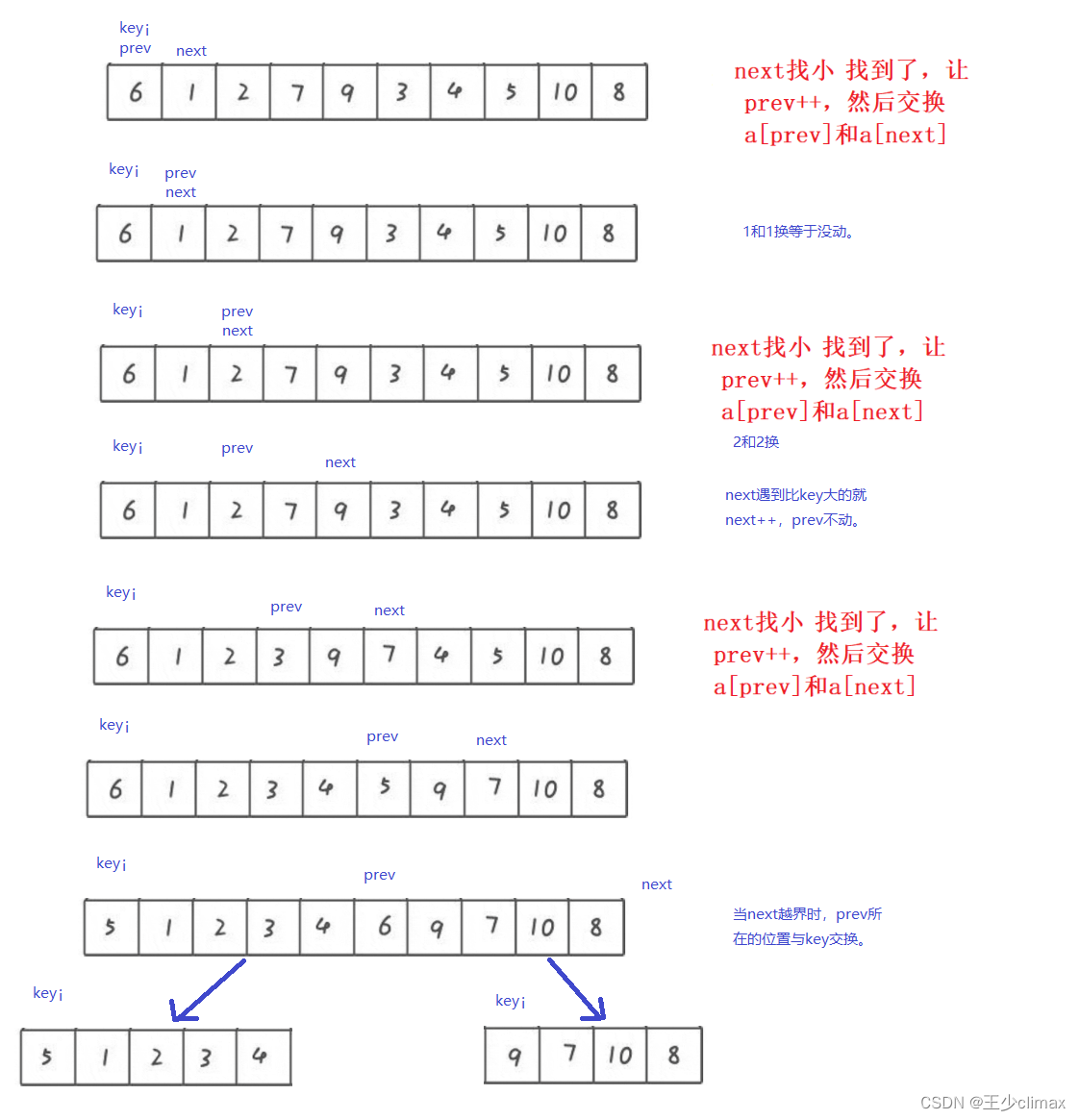
取最左边的下标左keyi,prev=begin、next=begin+1,
next找小,如果找到小于a[ keyi ]的数,就让prev++,
然后将a[prev]和a[next]交换。直到next大于n,结束。
最后再让a[keyi]和a[prev]交换。
int Q_PartSort3(int* a, int begin, int end)//前后指针法
{
int keyi = begin;
int prev = begin;
int next = begin + 1;
while (next <= end)
{
if (a[next] < a[keyi] && ++prev != next)
{
Swap(&a[prev], &a[next]);
}
next++;
}
Swap(&a[keyi], &a[prev]);
return prev;
}
void _QuickSort(int* a, int begin, int end)//递归
{
if (begin >= end)
{
return;
}
int keyi = Q_PartSort3(a, begin, end);
_QuickSort(a, begin, keyi - 1);
_QuickSort(a, keyi + 1, end);
}
快速排序优化
- 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序

快速排序非递归
void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (StackEmpty(&st) != 0)
{
right = StackTop(&st);
StackPop(&st);
left = StackTop(&st);
StackPop(&st);
if(right - left <= 1)
continue;
int div = PartSort1(a, left, right);
// 以基准值为分割点,形成左右两部分:[left, div) 和 [div+1, right)
StackPush(&st, div+1);
StackPush(&st, right);
StackPush(&st, left);
StackPush(&st, div);
}
StackDestroy(&s);
}
排序的代码
我的全部代码,拿走不谢!
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#define MAX 10
void display(int arr[], int num) {//遍历数组
int i;
for (i = 0; i < num; i++) {
printf("%-5d", arr[i]);
}
printf("\n");
return;
}
int Q_PartSort1(int* a, int begin, int end)//hoare
{
int keyi = begin;
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] >= a[keyi])//右边找小于a[keyi]的数
{
right--;
}
while (left < right && a[left] <= a[keyi])//左边找大于a[keyi]的数
{
left++;
}
Swap(&a[left], &a[right]);
}
//将a[keyi]与相遇点交换(要保证相遇点比a[keyi]小,需要让right先走)
Swap(&a[keyi], &a[right]);
/*Q_PartSort1(a, begin, keyi-1);
Q_PartSort1(a, keyi+1,end);*/
return right;
}
int Q_PartSort2(int* a, int begin, int end)//挖坑法
{
int key = a[begin];
int hole = begin;
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
int Q_PartSort3(int* a, int begin, int end)//前后指针法
{
int keyi = begin;
int prev = begin;
int next = begin + 1;
while (next <= end)
{
if (a[next] < a[keyi] && ++prev != next)
{
Swap(&a[prev], &a[next]);
}
next++;
}
Swap(&a[keyi], &a[prev]);
return prev;
}
void _QuickSort(int* a, int begin, int end)//递归
{
if (begin >= end)
{
return;
}
int keyi = Q_PartSort3(a, begin, end);
_QuickSort(a, begin, keyi - 1);
_QuickSort(a, keyi + 1, end);
}
int main()
{
return 0;
}