《数据结构》实验报告-实验二 栈与队列的应用

一、问题分析

（1）实验1中，火车进站和出站的过程，与后进先出的数据结构栈很相似。因为火车只能单方向进出站，前面进来的火车反而要等后面的火车先出站，这也导致火车出站的序列需要满足一定的条件。问题中给出进站和出站的序列，在计算机中可以用进栈和退栈模拟出来，如果最后不能按所给的出站序列退栈，则输出不可行。所以实验1是围绕栈展开讨论的，需要完成初始化栈，进栈，弹栈，获取栈顶元素，判断栈空等基本操作。
（2）实验2中，火车进站的顺序是乱序排列的，而要求出站的序列为升序，即序号小的永远要比序号大的先出站，这时就需要先进站的大序号火车在缓冲轨道上排队，等待小序号火车优先通过。而对于每条轨道，先进站的火车要比后进站的火车先出站，满足先进先出的队列结构。所以每条轨道上的火车从前往后序号是递增的。实质上就是求入栈序列中最长下降子序列长度。我们需要为每条缓冲轨道都设置一个队列，进行队列中队尾元素的比较，来确定后进来的火车到底从哪条缓冲轨道上驶入（入队操作）。所以实验2围绕队列展开，需要初始化队列，入队，获取队尾等操作。

二、详细设计

2.1设计思想
（1）实验1的实现需要用到栈，算法设计时用栈去模拟火车进站和出站的序列。首先使用两个数组in和out来保存进站与出站序列，再用inNum和outNum分别记录当前要进站的火车序号和当前要出站火车序号。当序号为inNum的火车进站时，先检查是否与序号为outNum的火车相同，如果相同就直接让outNum增一，表示这辆火车刚进站就马上出站了，甚至不用进栈保存；否则就要先进栈保存，因为这辆火车还未到出站时候。每次循环都检查栈顶火车序号与outNum的火车序号是否相同，如果相同就退栈（出站），直到不同为止。出站序列不可行的情况是当进入最后一辆火车并且执行完上述操作后，栈不为空（说明火车无法按照此序列出站），则输出不可行。
（2）实验2则需要使用队列数组来记录缓冲轨道的火车进站情况。而对于每一条轨道上的火车，排在后面的火车必须比它前面的火车序号要大，否则不能满足升序出站的条件。所以每次有火车进站时，先找到第一个队尾火车序号小于当前进站火车序号的轨道编号（队列数组下标），将该火车入队。如果找不到，这说明需要另开设一条轨道放置这列火车。这样的进站规定可以使得队列数组呈现两种有序性：
①队列内从队头到队尾的火车序号为升序
②队列数组的队尾元素相对于队列数组下标为降序
两个有序性使得我们可以用二分答案来寻找最优的轨道放置火车，将原来
O（n）的时间复杂度压缩到O（log2n）。最后输出已使用的轨道数即为所求。
2.2 存储结构及操作
2.2.1存储结构
2.2.1.1 实验1
栈的节点结构体sNode，包含：
（1）一个int类型变量id，表示火车的序号
（2）一个sNode类型的指针next，指向它在栈中的下个节点
自定义链栈的结构体Stack，包含：
（1）一个sNode类型的指针top，指向栈顶节点
（2）一个int类型变量size，表示栈已存的节点数
2.2.1.2 实验2
队列的节点结构体qNode，包含：
（1）一个int类型变量id，表示火车的序号
（2）一个qNode类型指针next，指向它在队列中的下个节点
自定义队列的结构体Queue，包含：
（1）一个qNode类型的指针front，指向队列的队头
（3）一个qNode类型的指针rear，指向队列的末尾
（2）一个int类型变量size，表示队列已存的节点数

2.2.2 涉及的操作
（1）实验1中的栈相关函数，如表1所示。

（2）实验2中的队列相关函数，如表2所示。

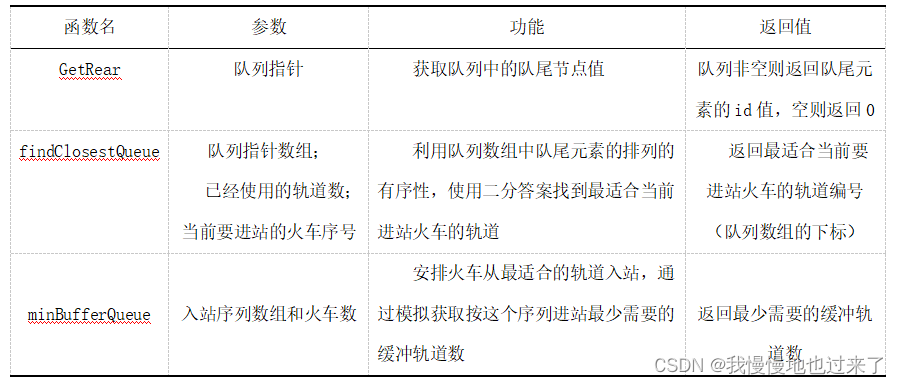
2.3 程序整体流程
（1）实验整体流程图如图1所示。

图 1
（2）实验1关键算法流程图，如图2所示。

图 2
（3）实验2关键算法流程图，如图3所示。

图 3

三、用户手册

程序接收数据的方式是从一个名为“Train.in”文件中读入。输入格式为先输入一个数n，表示总共要进站的火车数。然后有两行输入：第一行有n个数，在实验1中表示火车进站序列，在实验2中是无用数据（可以输入任意n个数）；第二行有n个数，在实验1中表示要判断是否火车的出站序列，在实验2中表示火车的乱序进站序列。当输入的数据中包含非法字符时，会显示：
The input data is illegal,please input again:
当获取到所有正确输入时，程序会输出当前的情况数（作为间隔符），若为第一次执行，输出如下：
Case 1
程序会先进行出站序列的可行性判断。如果火车可以按照该出站序列出站，则程序会输出：
Experiment 1 :Judge Possibility:
The output train sequence is Possible
否则，程序会输出相反的结果：
Experiment 1 :Judge Possibility:
The output train sequence is impossible
判断结束后，程序会计算火车以此乱序进站序列并按升序出站所需最少缓冲轨道，如果这个轨道数为1，计算结束后会输出：
Experiment 2:Get MinBuffer:
The recover the order,1 buffer queue is needed
至此完整的执行了一次情况，当仍有输入时情况数会增一，直到读到文件末尾才会终止程序。

四、结果

（1）“Train.in”文件内的测试数据，如图4和图5所示。

图 4

图 5
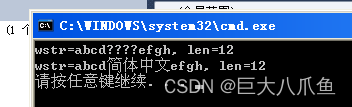
（2）程序运行截图，如图6和图7所示。

图 6
图 7

五、总结

本次实验中主要用到了栈和队列这两种极其重要的数据结构。对于栈，主要用到的操作有初始化链栈，压栈，弹栈，取栈顶和判断栈空；对于队列，主要的操作有初始化队列，入队，出队，返回队尾和判断队空。在实现数据结构的基本操作的基础上，把实际的问题转化为对栈和队列的操作上。在实验1中，火车进出站的过程在栈中得到很好地模拟，利用栈的特性就可以很轻松的判断给出的出站序列是否可行；在实验2中，更多的利用了队列先进先出的思想，而不是简单的模拟。特别在寻找最佳轨道入队时，运用到的其实是利用队列数组队尾元素的有序性，进行二分答案找到最佳轨道。
然而在实验2中，存在许多明显的问题。比如在初始化队列数组时，将火车总数个队列进行了初始化，这在火车总数较大的时候会造成巨大的空间开销，且大多数时候都是用不完的，利用率较低。但是其实我们并不需要用一个队列数组来存储火车序列。因为我们对于每条轨道上的火车，只关心它最末尾那辆火车的序号大小，在程序中也完全没有用到出队和取队头元素的操作。所以我们可以用一个普通的数组来存储各轨道的队尾火车序号，在二分答案时找到最佳轨道时，只需替代掉对应数组下标的数即可，表示该火车驶入了该轨道。这样不仅大大降低了空间复杂度，而且也不需要进行各种队列操作，简化了操作。这其实是建立在队列思想基础上的优化。
通过本次实验，我巩固了进行栈和队列的基本操作的能力，在思考问题时代入特定的数据结构，构建了解题的框架，编写时几乎没出现什么bug。在实验2中，我对老师给出的模板效率提出了自己的见解，培养了独立思考的能力。在完成实验报告的过程中，逐渐规范文章格式，为各个图片和表格插入题注，对字体和大小严格要求，并培养了良好的流程图作图习惯。相信通过本次实验，我可以为未来的学习打下更坚实的基础。