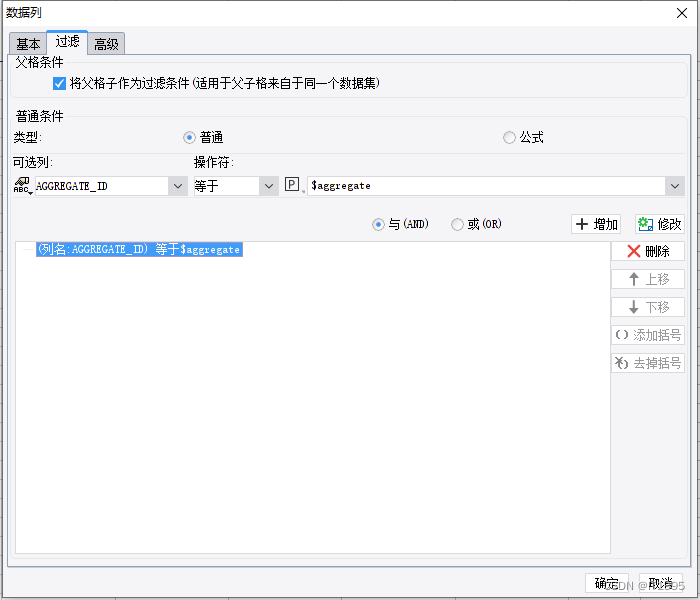
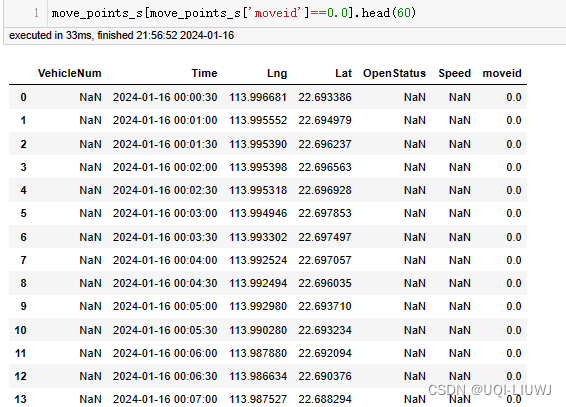
图像处理-孤立点的检测
孤立点的检测在图像处理中通常涉及到检测图像中的突变或者边缘,而使用二阶导数是一种常见的方法。一阶导数可以帮助找到图像中的边缘,而二阶导数则有助于检测边缘上的峰值,这些峰值可能对应于孤立点或者特殊的图像结构。
在二阶导数的情况下,通常使用Laplacian算子。Laplacian算子用于计算图像中每个像素位置的二阶导数。在离散的图像上,Laplacian算子的一种常见表示如下:
Δ
I
=
I
x
x
+
I
y
y
\Delta I = I_{xx} + I_{yy}
ΔI=Ixx+Iyy
其中,
I
x
x
I_{xx}
Ixx 和
I
y
y
I_{yy}
Iyy 是图像在水平和垂直方向上的二阶导数。
对于孤立点检测,我们可以关注图像中二阶导数的峰值,这些峰值可能表示图像中的尖锐变化或者突变,进而对应于孤立点或者边缘。一种常见的方法是通过计算Laplacian的绝对值或者平方来获取边缘强度:
E
d
g
e
I
n
t
e
n
s
i
t
y
=
∣
Δ
I
∣
或
E
d
g
e
I
n
t
e
n
s
i
t
y
=
(
Δ
I
)
2
EdgeIntensity = |\Delta I|\ 或 \ EdgeIntensity=(\Delta I)^2
EdgeIntensity=∣ΔI∣ 或 EdgeIntensity=(ΔI)2
在实际应用中,为了避免噪声对结果的影响,通常会在应用二阶导数之前进行平滑操作,例如使用高斯滤波。这有助于去除图像中的高频噪声。
下面是一个简单的Python示例,使用SciPy中的Laplacian算子进行二阶导数计算:
import numpy as np
from scipy.ndimage import convolve
import matplotlib.pyplot as plt
# 生成一个包含孤立点的示例图像
image = np.zeros((100, 100))
image[50, 50] = 255 # 在图像中央放置一个孤立点
# 计算Laplacian(二阶导数)
laplacian = convolve(image, np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]))
# 可视化结果
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[1].imshow(np.abs(laplacian), cmap='gray')
axes[1].set_title('Laplacian (Absolute)')
plt.show()
结果输出:

这个示例中,生成了一个包含孤立点的图像,并使用Laplacian算子计算了图像的二阶导数。最后,通过取绝对值可视化Laplacian的结果。在实际应用中,可能需要根据图像的特性进行调整和优化 Laplacian 的参数,比如某些图像中的点检测:
laplacian = convolve(image, np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]]))