🔗 运行环境:Matlab
🚩 撰写作者:左手の明天
🥇 精选专栏:《python》
🔥 推荐专栏:《算法研究》
🔐#### 防伪水印——左手の明天 ####🔐
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天分享Matlab深度学习——波形分割💗
📆 最近更新:2024 年 01 月 15 日,左手の明天的第 312 篇原创博客
📚 更新于专栏:matlab
🔐#### 防伪水印——左手の明天 ####🔐
🚩接上上一篇文章 详解Matlab深度学习进行波形分割
使用滤波后的 ECG 信号训练网络
使用与以前相同的网络架构基于滤波后的 ECG 信号训练 LSTM 网络。
if actionFlag == "Train networks"
filteredNet = trainNetwork(filteredTrainSignals,trainLabels,layers,options);
end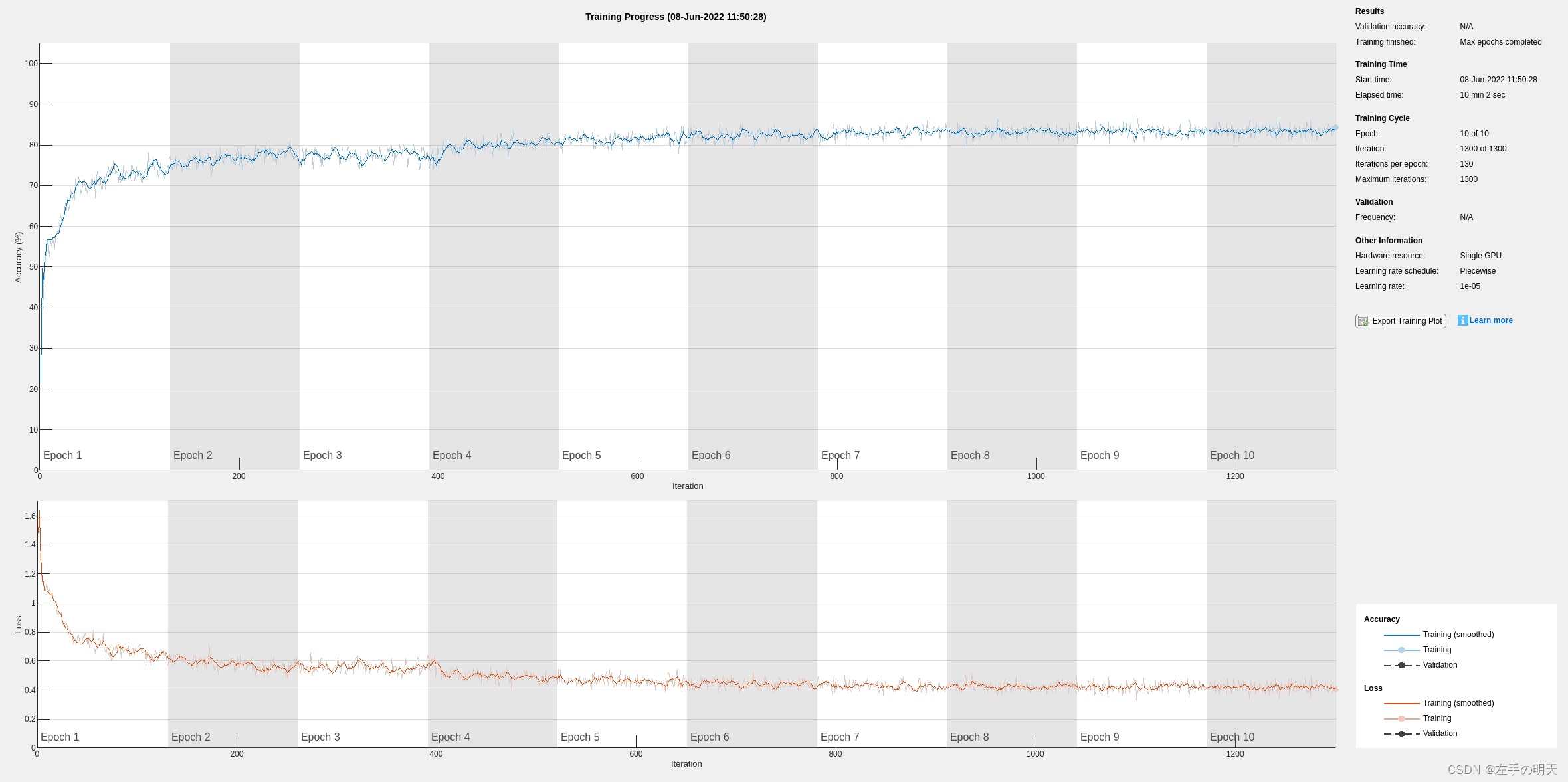
信号预处理将训练准确度提高到 80% 以上。
对滤波后的 ECG 信号进行分类
用更新后的 LSTM 网络对预处理后的测试数据进行分类。
predFilteredTest = classify(filteredNet,filteredTestSignals,'MiniBatchSize',50);将分类性能可视化为混淆矩阵。
figure
confusionchart([testLabels{:}],[predFilteredTest{:}],'Normalization','row-normalized');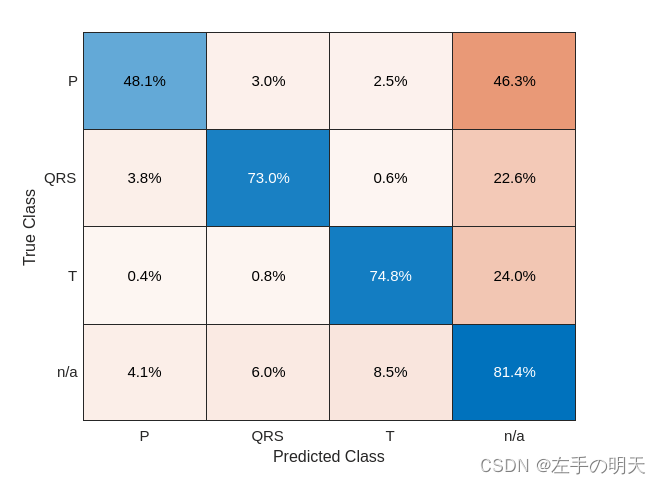
简单的预处理将 T 波分类提高了约 15%,将 QRS 复波和 P 波分类提高了约 10%。
ECG 信号的时频表示
时间序列数据成功分类的常见方法是提取时频特征并将其馈送到网络而不是原始数据。然后,网络同时跨时间和频率学习模式。
傅里叶同步压缩变换 (FSST) 计算每个信号采样的频谱,因此对于需要保持与原始信号相同的时间分辨率的分割问题,它是可直接使用的理想选择。使用 fsst 函数检查一个训练信号的变换。指定长度为 128 的凯塞窗以提供足够的频率分辨率。
data = preview(trainDs);
figure
fsst(data{1,1},250,kaiser(128),'yaxis')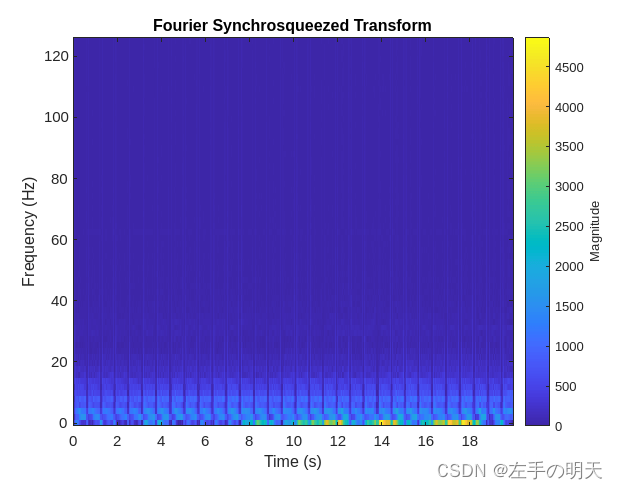
基于感兴趣的频率范围 [0.5, 40] Hz 计算训练数据集中每个信号的 FSST。将 FSST 的实部和虚部视为单独的特征,并将两个分量都馈送到网络中。而且,通过减去均值并除以标准差来标准化训练特征。使用变换后的数据存储、extractFSSTFeatures 辅助函数和 tall 函数来并行处理数据。
fsstTrainDs = transform(trainDs,@(x)extractFSSTFeatures(x,250));
fsstTallTrainSet = tall(fsstTrainDs);
fsstTrainData = gather(fsstTallTrainSet);Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: 0% complete Evaluation 0% complete - Pass 1 of 1: 4% complete Evaluation 4% complete - Pass 1 of 1: 8% complete Evaluation 8% complete - Pass 1 of 1: 12% complete Evaluation 12% complete - Pass 1 of 1: 17% complete Evaluation 17% complete - Pass 1 of 1: 21% complete Evaluation 21% complete - Pass 1 of 1: 25% complete Evaluation 25% complete - Pass 1 of 1: 29% complete Evaluation 29% complete - Pass 1 of 1: 33% complete Evaluation 33% complete - Pass 1 of 1: 38% complete Evaluation 38% complete - Pass 1 of 1: 42% complete Evaluation 42% complete - Pass 1 of 1: 46% complete Evaluation 46% complete - Pass 1 of 1: 50% complete Evaluation 50% complete - Pass 1 of 1: 54% complete Evaluation 54% complete - Pass 1 of 1: 58% complete Evaluation 58% complete - Pass 1 of 1: 62% complete Evaluation 62% complete - Pass 1 of 1: 67% complete Evaluation 67% complete - Pass 1 of 1: 71% complete Evaluation 71% complete - Pass 1 of 1: 75% complete Evaluation 75% complete - Pass 1 of 1: 79% complete Evaluation 79% complete - Pass 1 of 1: 83% complete Evaluation 83% complete - Pass 1 of 1: 88% complete Evaluation 88% complete - Pass 1 of 1: 92% complete Evaluation 92% complete - Pass 1 of 1: 96% complete Evaluation 96% complete - Pass 1 of 1: 100% complete Evaluation 100% complete - Pass 1 of 1: Completed in 2 min 39 sec Evaluation 100% complete Evaluation completed in 2 min 39 sec
对测试数据重复此过程。
fsstTTestDs = transform(testDs,@(x)extractFSSTFeatures(x,250));
fsstTallTestSet = tall(fsstTTestDs);
fsstTestData = gather(fsstTallTestSet);Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 1 min 8 sec Evaluation completed in 1 min 8 sec
调整网络架构
修改 LSTM 架构,使网络接受每个采样的频谱,而不是单一值。检查 FSST 的大小以查看频率的数量。
size(fsstTrainData{1,1})ans = 1×2
40 5000
指定一个包含 40 个输入特征的 sequenceInputLayer。保持其余网络参数不变。
layers = [ ...
sequenceInputLayer(40)
lstmLayer(200,'OutputMode','sequence')
fullyConnectedLayer(4)
softmaxLayer
classificationLayer];使用 ECG 信号的 FSST 训练网络
使用变换后的数据集训练更新后的 LSTM 网络。
if actionFlag == "Train networks"
fsstNet = trainNetwork(fsstTrainData(:,1),fsstTrainData(:,2),layers,options);
end
使用时频特征提高了训练准确度,现在已超过 90%。
用 FSST 对测试数据进行分类
使用更新后的 LSTM 网络和提取的 FSST 特征,对测试数据进行分类。
predFsstTest = classify(fsstNet,fsstTestData(:,1),'MiniBatchSize',50);将分类性能可视化为混淆矩阵。
confusionchart([fsstTestData{:,2}],[predFsstTest{:}],'Normalization','row-normalized'); 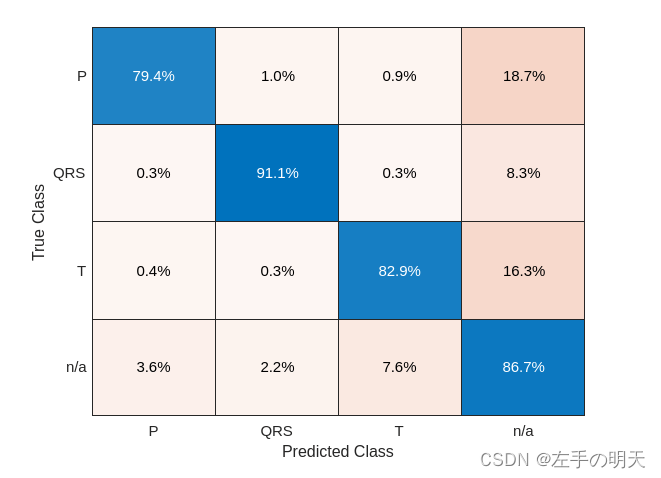
与原始数据结果相比,使用时间频率表示法将 T 波分类提高了约 25%,将 P 波分类提高了约 40%,将 QRS 复波分类提高了 30%。
使用 signalMask 对象将网络预测与单个 ECG 信号的真实值标签进行比较。绘制感兴趣的区域时忽略 "n/a" 标签。
testData = gather(tall(testDs));Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 2.1 sec Evaluation completed in 2.2 sec
Mtest = signalMask(testData{1,2}(3000:4000));
Mtest.SpecifySelectedCategories = true;
Mtest.SelectedCategories = find(Mtest.Categories ~= "n/a");
figure
subplot(2,1,1)
plotsigroi(Mtest,testData{1,1}(3000:4000))
title('Ground Truth')
Mpred = signalMask(predFsstTest{1}(3000:4000));
Mpred.SpecifySelectedCategories = true;
Mpred.SelectedCategories = find(Mpred.Categories ~= "n/a");
subplot(2,1,2)
plotsigroi(Mpred,testData{1,1}(3000:4000))
title('Predicted')结论
此示例说明信号预处理和时频分析是如何提高 LSTM 波形分割性能的。带通滤波和基于傅里叶的同步压缩使所有输出类的平均改进程度从 55% 提高到 85% 左右。
参考资料
[1] McSharry, Patrick E., et al."A dynamical model for generating synthetic electrocardiogram signals."IEEE® Transactions on Biomedical Engineering.Vol. 50, No. 3, 2003, pp. 289–294.
[2] Laguna, Pablo, Raimon Jané, and Pere Caminal."Automatic detection of wave boundaries in multilead ECG signals:Validation with the CSE database."Computers and Biomedical Research.Vol. 27, No. 1, 1994, pp. 45–60.
[3] Goldberger, Ary L., Luis A. N. Amaral, Leon Glass, Jeffery M. Hausdorff, Plamen Ch.Ivanov, Roger G. Mark, Joseph E. Mietus, George B. Moody, Chung-Kang Peng, and H. Eugene Stanley."PhysioBank, PhysioToolkit, and PhysioNet:Components of a New Research Resource for Complex Physiologic Signals."Circulation.Vol. 101, No. 23, 2000, pp. e215–e220. [Circulation Electronic Pages; http://circ.ahajournals.org/content/101/23/e215.full].
[4] Laguna, Pablo, Roger G. Mark, Ary L. Goldberger, and George B. Moody."A Database for Evaluation of Algorithms for Measurement of QT and Other Waveform Intervals in the ECG."Computers in Cardiology.Vol.24, 1997, pp. 673–676.
[5] Sörnmo, Leif, and Pablo Laguna."Electrocardiogram (ECG) signal processing."Wiley Encyclopedia of Biomedical Engineering, 2006.
[6] Kohler, B-U., Carsten Hennig, and Reinhold Orglmeister."The principles of software QRS detection."IEEE Engineering in Medicine and Biology Magazine.Vol. 21, No. 1, 2002, pp. 42–57.
[7] Salamon, Justin, and Juan Pablo Bello."Deep convolutional neural networks and data augmentation for environmental sound classification."IEEE Signal Processing Letters.Vol. 24, No. 3, 2017, pp. 279–283.