丑数Ⅱ
题目要求

解题思路
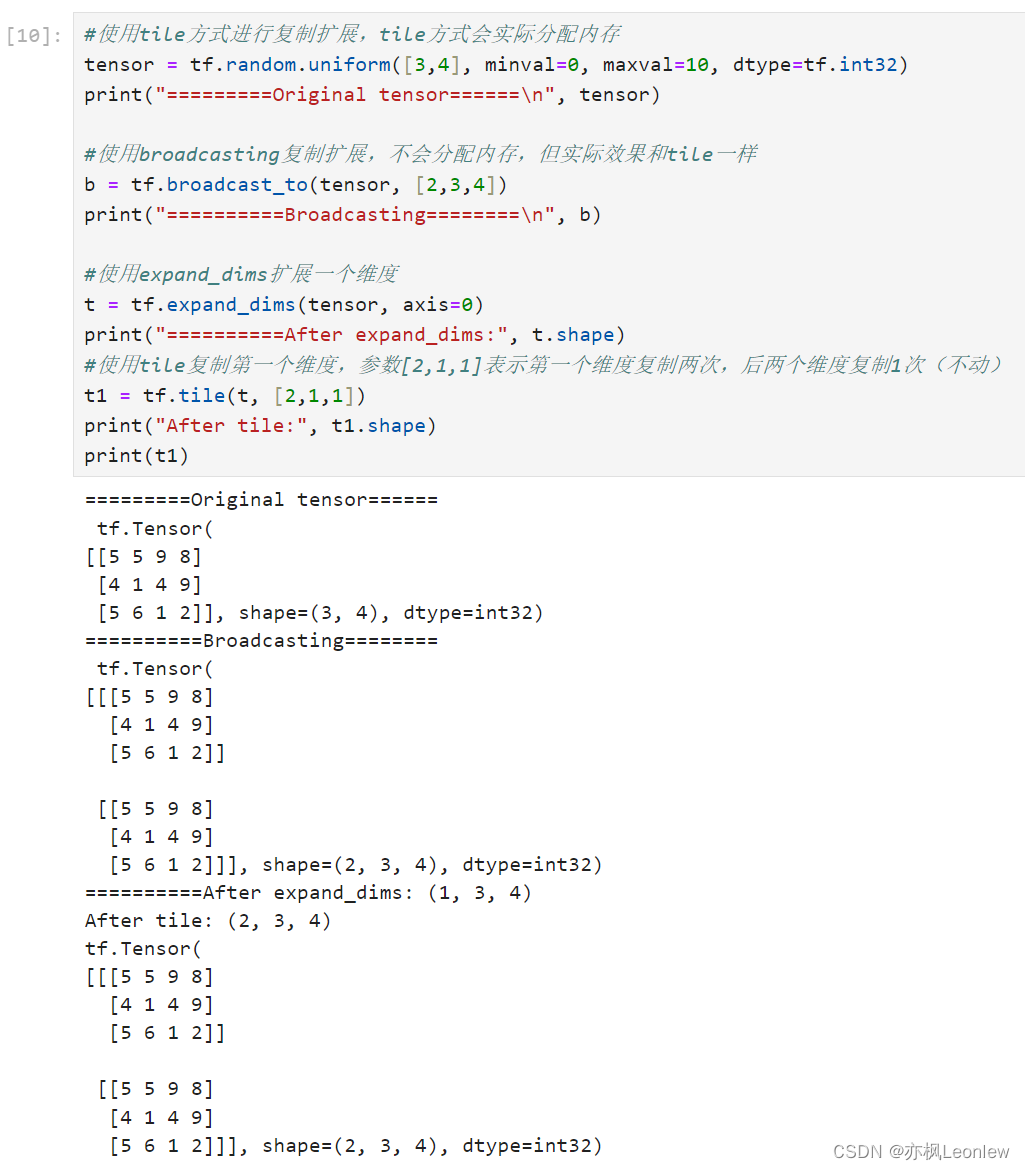
题目的要求是让我们生成第n个丑数。如果考虑逐个遍历自然数是否为丑数,一定会超时。这里推荐使用生成的办法。
要生成第n个丑数,我们必须从第一个丑数1开始,向后逐渐的寻找。丑数只包含2,3,5三个因子,所以生成方式是在已经生成的丑数集合中乘以[2,3,5]而得到新的丑数。
现在的问题是在已经生成的丑数集合中,用哪个数字乘以2?用哪个数字乘以3?用哪个数字乘以5?
很显然的一个结论:用还没乘过2的最小丑数乘以2;用还没乘过3的最小丑数乘以3;用还没乘过5的最小丑数乘以5。然后在得到的数字中取最小,就是新的丑数。
实现的方法是用动态规划:
- 我们需要定义3个指针index2,index3,index5分别表示丑数集合中还没乘过2,3,5的丑数位置。
- 然后每次新的丑数
dp[i]=min(dp[index2]*2,dp[index3]*3,dp[index5]*5) - 最后根据dp[i]是由index2,index3,index5中哪个相乘得到的,对应的把此index+1,表示还没乘过该index的最小丑数变大了。
代码
class Solution:
def nthUglyNumber(self, n: int) -> int:
if n < 0:
return 0
index2,index3,index5=0,0,0
dp=[1] *n
for i in range(1,n):
dp[i]=min(2 * dp[index2],3 * dp[index3], 5 * dp[index5])
if dp[i] == 2*dp[index2]: index2 +=1
if dp[i] == 3*dp[index3]: index3 +=1
if dp[i] == 5*dp[index5]: index5 +=1
return dp[n-1]
复杂度分析
时间复杂度:
O
(
N
)
O(N)
O(N)
空间复杂度:
O
(
N
)
O(N)
O(N)