《深度学习进阶自然语言处理》第五章：RNN通俗介绍

文章目录

- - 5.1 概率和语言模型
  - - 5.1.1 概率视角下的word2vec
    - 5.1.2 语言模型
    - 5.1.3 将CBOW模型用作语言模型的效果怎么样？
  - 5.2 RNN
  - - 5.2.1 循环神经网络
    - 5.2.2 展开循环
    - 5.2.3 Backpropagation Through Time
    - 5.2.4 Truncated BPTT
    - 5.2.5 Truncated BPTT的mini-batch学习
  - 5.3 RNN的实现
  - 5.4 RNNLM的学习与评价
  - - 5.4.1 RNNLM的实现
    - 5.4.2 语言模型的评价
  - 5.5 小结

之前文章链接：

开篇介绍：《深度学习进阶自然语言处理》书籍介绍
第一章：《深度学习进阶自然语言处理》第一章：神经网络的复习
第二章：《深度学习进阶自然语言处理》第二章：自然语言和单词的分布式表示
第三章：《深度学习进阶自然语言处理》第三章：word2vec
第四章：《深度学习进阶自然语言处理》第四章：Embedding层和负采样介绍

我们之前在介绍神经网络的时候，一般以CNN举例。那么CNN和接下来要介绍的RNN(Recurrent Neural Network)有什么区别呢？

其实CNN是一种典型的前馈型神经网络。前馈 (feedforward）是指网络的传播方向是单向的。具体地说，先将输入信号传给下一层（隐藏层)，接收到信号的层也同样传给下一层，然后再传给下一层⋯⋯像这样，信号仅在一个方向上传播。

这类型前馈神经网络在处理时间序列数据的时候，效果并不好，其无法充分学习时序数据的性质，但是该问题恰好RNN可以解决。那么，接下来我们一起看一下RNN的结构。

5.1 概率和语言模型

5.1.1 概率视角下的word2vec

在介绍RNN之前，我们先复习一下上一章的word2vec, 以CBOW为例，该模型所做的事情就是从上下文（wt-1和 wt+1）预测目标词（wt)。整体结构如下图：

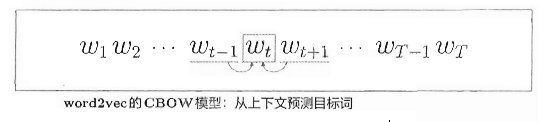
用数学式来表示“当给定wt-1，和wt+1时目标词是wt的概率”：

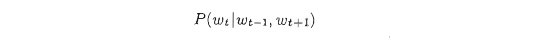
如果把CBOW中的上下文限定为左侧窗口，则如下图：

在仅将左侧2 个单词作为上下文的情况下，CBOW 模型输出的概率如下：

现在我们已经通过概率表示了CBOW模型，那么其是否可以在语言模型中发挥作用呢？在讨论这个问题前，我们先一起看一下什么是语言模型。

5.1.2 语言模型

语言模型（languege model）给出了单词序列发生的概率。具体来说，就是使用概率来评估一个单词序列发生的可能性，即在多大程度上是自然的单词序列。比如，对于“you say goodbye”这一单词序列，语言模型给出高概率（比如0.092)；对于 “you say good die“这一单词序列，模型则给出低概率（比如0.000 000 000 003 2)。

那么具体怎么求解这个概率呢，我们先从一个单词入手，求解一个单词的概率可以表示为：

当知道一个单词的概率之后，我们可以通过联合概率公式，求出一句话的概率：P（ $w_1,……，w_m$ ）.

5.1.3 将CBOW模型用作语言模型的效果怎么样？

到此时，我们的推导依旧可行，那么我们一起看一下如果继续按照这种方法推导会有什么问题。

以下面图中为例：

在上举例中，“Tom 在房间看电视，Mary进了房间”。根据该语境（上下文)，正确答案应该是 Mery 向 Tom（或者 “him”）打招呼。这里要获得正确答案，就必须将“？”前面第 18个单词处的 Tom 记住。如果 CBOW 模型的上下文大小是10，则这个问题将无法被正确回答。

那么，是否可以通过增大 CBOW 模型的上下文大小（比如变为20或 30）来解决此问题呢？

的确，CBOW 模型的上下文大小可以任意设定，但是CBOW模型还存在忽视了上下文中单词顺序的问题。

CBOW 是 Continuous Bag-Of-Words 的简称.Bag-Of-Words是 '一袋子单词"的意思,这意味着袋子中单词的顺序被忽视了.

那么，如何解决这里提出的问题呢？

这就轮到 RNN 出场了。RNN 具有一个机制，那就是无论上下文有多长，都能将上下文信息记住。因此，使用RNN 可以处理任意长度的时序数据。下面，我们就来感受一下 RNN 的魅力。

5.2 RNN

5.2.1 循环神经网络

总算要介绍RNN的结构，无需赘言，直接上图：

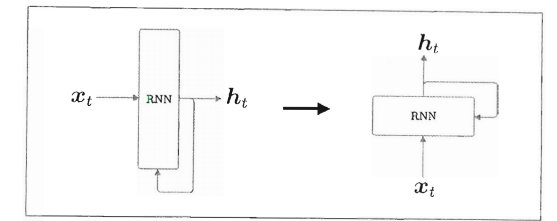
如上左图所示，RNN 层有环路。通过该环路，数据可以在层内循环。时刻t的输入是 $x_t$ ，这暗示着时序数据 $x_0，x_1，……，x_t，……）$ 会被输入到层中。然后，以与输人对应的形式，输出 $h_0， h_1，……，h_t，……)$ 。

这里假定在各时刻向 RNN 层输入的 $x_t$ 是向量。比如，在处理句子（单词序列）的情况下，将各个单词的分布式表示（单词向量）作为xt输入 RNN层。

为了后面更好表达，对上图左侧图形旋转90度得到上图右侧结果，其他均相同。

5.2.2 展开循环

为了更好理解，把循环结构展开：

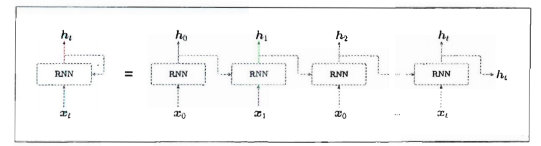
各个时刻的 RNN 层接收传给该层的输入和前一个 RNN 层的输出，然后据此计算当前时刻的输出，此时进行的计算可以用下式表示：

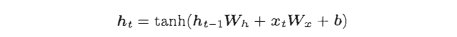
首先说明一下上式中的符号。RNN 有两个权重，分别是将输入 x 转化为输出 h 的权重 Wx 和将前一个 RNN 层的输出转化为当前时刻的输出的权重 Wh。此外，还有偏置b。这里，ht-1和xt都是行向量。

在上式中，首先执行矩阵的乘积计算，然后使用 tanh 函数（双曲正切函数）变换它们的和，其结果就是时刻t的输出 $h_t$ 。这个 $h_t$ 一方面向上输出到另一个层，另一方面向右输出到下一个 RNN层（自身）。

观察该式可以看出，现在的输出 $h_t$ 是由前一个输出 $h_{t-1}$ 计算出来的。从另一个角度看，这可以解释为，RNN 具有“状态”h，并以该表达式的形式被更新。这就是说RNN层是“具有状态的层”或“具有存储（记忆）的层”的原因。

5.2.3 Backpropagation Through Time

将 RNN 层展开后，就可以视为在水平方向上延伸的神经网络，因此 RNN 的学习可以用与普通神经网络的学习相同的方式进行。

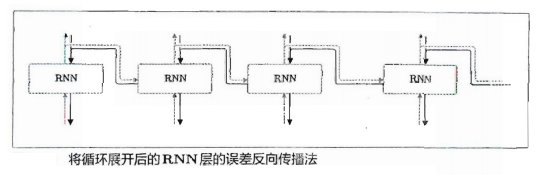
因为这里的误差反向传播法是“按时间顺序展开的神经网络的误差反向传播法”，所以称为 Backpropegation Through Time(基于时间的反向传播），简称 BPTT。

5.2.4 Truncated BPTT

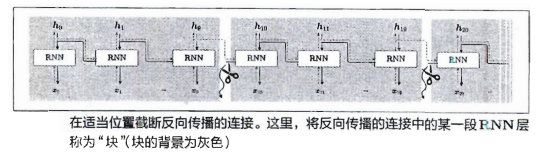
在处理长时序数据时，通常的做法是将网络连接截成适当的长度。具体来说，就是将时间轴方向上过长的网络在合适的位置进行截断，从而创建多个小型网络，然后对截出来的小型网络执行误差反向传播法，这个方法称为 Truncated BPTT（截断的 BPTT)。

在 Truncated BPTT 中，网络连接被截断，但严格地讲，只是网络的反向传播的连接被截断，正向传播的连接依然被维持，这一点很重要。也就是说，正向传播的信息没有中断地传播。与此相对，反向传播则被截断为适当的长度，以被截出的网络为单位进行学习。

5.2.5 Truncated BPTT的mini-batch学习

到目前为止，我们在探讨 Truncated BPTT 时，并没有考虑 mini-batch 学习。换句话说，我们之前的探讨对应于批大小为1的情况。为了执行 mini-batch 学习，需要考虑批数据，让它也能按顺序输入数据。因此，在输入数据的开始位置，需要在各个批次中进行“偏移“。

具体偏移方式，我们通过举例说明，假设对长度为 1000的时序数据，以时间长度10为单位进行截断。此时如何将批大小设为2进行学习呢？在这种情况下，作为 RNN 层的输入数据，第1笔样本数据从头开始按顺序输入，第2笔数据从第 500 个数据开始按顺序输入。也就是说，将开始位置平移500，如下图：

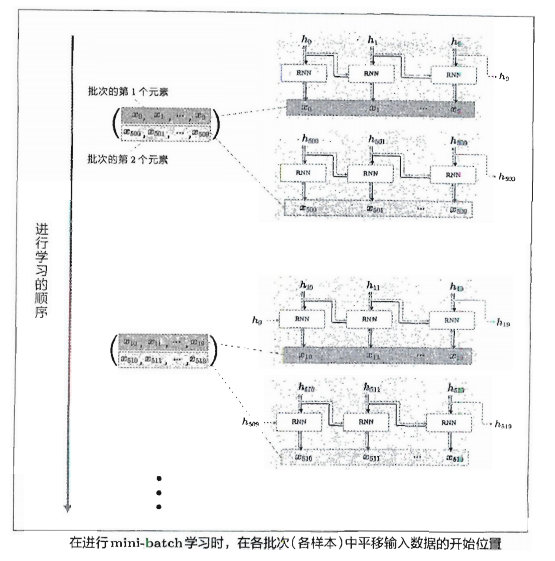
上图中，批次的第1个元素是x0，……，x9，批次的第2个元素是x500，……，x509，将这个 mini-batch 作为 RNN 的输入数据进行学习。因为要输入的数据是按顺序的，所以接下来是时序数据的第10~19 个数据和第510~519 个数据，像这样，在进行 mini-batch 学习时，平移各批次输入数据的开始位置，按顺序输入。

5.3 RNN的实现

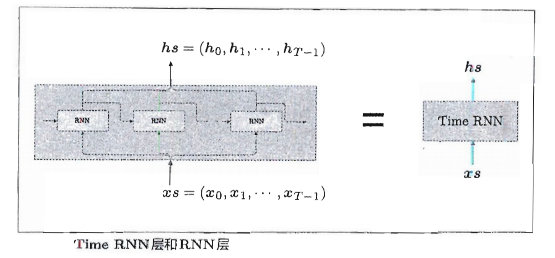
关于RNN的实现，在此不做详述，我们展示了RNN和TimeRNN两个类的实现过程。其中RNN层实现了RNN的单步处理；TimeRNN层由T个RNN层构成，如下图：

# 部分代码，所有代码见书本附件代码

class RNN:
    def __init__(self, Wx, Wh, b):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = None

    def forward(self, x, h_prev):
        Wx, Wh, b = self.params
        t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b
        h_next = np.tanh(t)

        self.cache = (x, h_prev, h_next)
        return h_next

    def backward(self, dh_next):
        Wx, Wh, b = self.params
        x, h_prev, h_next = self.cache

        dt = dh_next * (1 - h_next ** 2)
        db = np.sum(dt, axis=0)
        dWh = np.dot(h_prev.T, dt)
        dh_prev = np.dot(dt, Wh.T)
        dWx = np.dot(x.T, dt)
        dx = np.dot(dt, Wx.T)

        self.grads[0][...] = dWx
        self.grads[1][...] = dWh
        self.grads[2][...] = db

        return dx, dh_prev


class TimeRNN:
    def __init__(self, Wx, Wh, b, stateful=False):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.layers = None

        self.h, self.dh = None, None
        self.stateful = stateful

    def forward(self, xs):
        Wx, Wh, b = self.params
        N, T, D = xs.shape
        D, H = Wx.shape

        self.layers = []
        hs = np.empty((N, T, H), dtype='f')

        if not self.stateful or self.h is None:
            self.h = np.zeros((N, H), dtype='f')

        for t in range(T):
            layer = RNN(*self.params)
            self.h = layer.forward(xs[:, t, :], self.h)
            hs[:, t, :] = self.h
            self.layers.append(layer)

        return hs

    def backward(self, dhs):
        Wx, Wh, b = self.params
        N, T, H = dhs.shape
        D, H = Wx.shape

        dxs = np.empty((N, T, D), dtype='f')
        dh = 0
        grads = [0, 0, 0]
        for t in reversed(range(T)):
            layer = self.layers[t]
            dx, dh = layer.backward(dhs[:, t, :] + dh)
            dxs[:, t, :] = dx

            for i, grad in enumerate(layer.grads):
                grads[i] += grad

        for i, grad in enumerate(grads):
            self.grads[i][...] = grad
        self.dh = dh

        return dxs

    def set_state(self, h):
        self.h = h

    def reset_state(self):
        self.h = None

5.4 RNNLM的学习与评价

5.4.1 RNNLM的实现

在此我们实现一个简单RNN语言模型，其结构图如下：

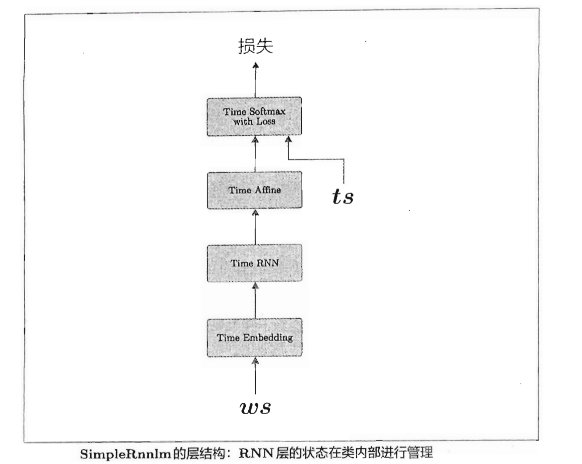
实现代码如下：

# 部分代码，所有代码见书本附件代码

# coding: utf-8
import sys
sys.path.append('..')
import numpy as np
from common.time_layers import *


class SimpleRnnlm:
    def __init__(self, vocab_size, wordvec_size, hidden_size):
        V, D, H = vocab_size, wordvec_size, hidden_size
        rn = np.random.randn

        # 初始化权重
        embed_W = (rn(V, D) / 100).astype('f')
        rnn_Wx = (rn(D, H) / np.sqrt(D)).astype('f')
        rnn_Wh = (rn(H, H) / np.sqrt(H)).astype('f')
        rnn_b = np.zeros(H).astype('f')
        affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
        affine_b = np.zeros(V).astype('f')

        # 生成层
        self.layers = [
            TimeEmbedding(embed_W),
            TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
            TimeAffine(affine_W, affine_b)
        ]
        self.loss_layer = TimeSoftmaxWithLoss()
        self.rnn_layer = self.layers[1]

        # 将所有的权重和梯度整理到列表中
        self.params, self.grads = [], []
        for layer in self.layers:
            self.params += layer.params
            self.grads += layer.grads

    def forward(self, xs, ts):
        for layer in self.layers:
            xs = layer.forward(xs)
        loss = self.loss_layer.forward(xs, ts)
        return loss

    def backward(self, dout=1):
        dout = self.loss_layer.backward(dout)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)
        return dout

    def reset_state(self):
        self.rnn_layer.reset_state()

5.4.2 语言模型的评价

语言模型基于给定的己经出现的单词（信息）输出将要出现的单词的概率分布。困惑度（perplexity）常被用作评价语言模型的预测性能的指标。

简单地说，困惑度表示“概率的倒数”（这个解释在数据量为1时严格一致)。为了说明概率的倒数，我们仍旧考虑 “you say goodbye and i say hello。” 这一语料库。假设在向语言模型“模型1”传入单词 you 时会输出下图左图所示的概率分布。此时，下一个出现的单词是 say 的概率为0.8，这是一个相当不错的预测。取这个概率的倒数，可以计算出困惑度为1.25。而下图右侧的模型（“模型2”）预测出的正确单词的概率为0.2，这显然是一个很差的预测，此时的困惑度为5。

总结一下，“模型1” 能准确地预测，困感度是 1.25；“模型2” 的预测未能命中，困惑度是 5.0。此例表明，困感度越小越好。