数量技术宅团队在CSDN学院推出了量化投资系列课程

欢迎有兴趣系统学习量化投资的同学，点击下方链接报名：

量化投资速成营（入门课程）

Python股票量化投资

Python期货量化投资

Python数字货币量化投资

C++语言CTP期货交易系统开发

数字货币JavaScript语言量化交易系统开发

---

随着量化交易、高频交易的竞争日益激烈，事实证明，交易执行显着影响量化策略的投资绩效。 因此，许多从业者开始将交易执行视为一项独立的任务。 本期文章分享，我们搜寻了一些用于最小化交易成本的最佳交易订单执行策略算法相关的论文，供大家参考。

最优交易策略和供需动态

来自 Anna Obizhaeva 和 Jiang Wang的《Optimal Trading Strategy and Supply/Demand Dynamics》：

简介

市场上证券的供给/需求是一个跨期的而非静态的对象，其动态对于决定市场参与者的交易行为至关重要。 在该论文中的研究表明，供给/需求的动态，而不是其静态属性，对于给定订单的最优交易策略至关重要。 使用限价订单簿市场，该论文开发了一个简单的框架来模拟供需动态及其对执行成本的影响。 该论文表明，最佳执行策略涉及离散交易和连续交易，而不仅仅是先前工作所建议的连续交易。 与简单的连续策略相比，最优策略可以节省大量成本。 该论文还表明，关于最佳交易行为的预测可能会对观察到的日内交易量、波动性和价格行为产生有趣的影响。

研究结论

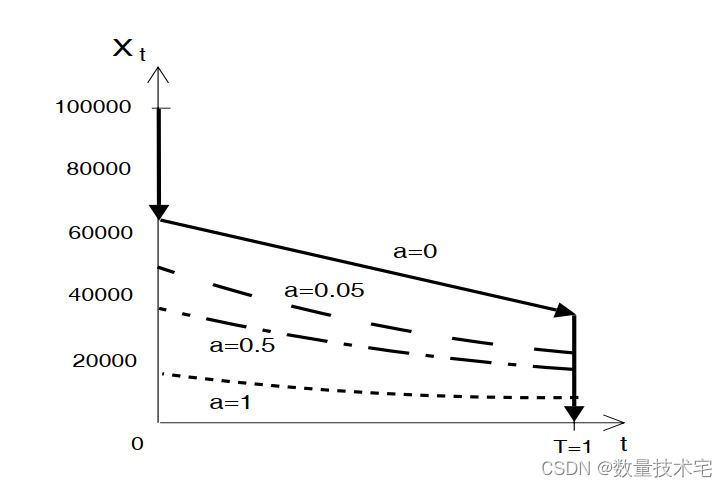
该论文分析了执行大订单的最佳交易策略。 该论文表明，先前工作中广泛使用的静态价格影响函数未能捕捉市场中证券供需的跨期性质。 该论文为限价订单簿市场构建了一个简单的动态模型，以捕获供需的跨期性质并求解最佳执行策略。 该论文表明，当选择最佳交易时间时，供需动态是确定最佳执行策略的关键因素。 与之前的工作相反，最佳执行策略涉及离散交易和连续交易，而不仅仅是连续交易。 这种交易行为与经验性的盘中成交量和价格模式是一致的。 该论文关于最佳执行策略的结果还表明了这些日内模式的可测试影响，并为市场流动性需求提供了新的见解。

该论文用于 LOB 动态的具体模型非常简单，因为该论文的目标主要是说明其重要性。 实际的 LOB 动态可能要复杂得多。 然而，该论文开发的框架相当通用，可以适应丰富形式的 LOB 动态。 此外，随着当前开放电子限价订单簿数量的增加，该论文的 LOB 模型可以轻松校准并用于解决现实世界的问题。

均值-方差最优自适应执行

来自 Julian Lorenz 和 Robert Almgren的《Mean-Variance Optimal Adaptive Execution》：

简介

股票和其他证券的电子交易大量使用“到达价格”算法，该算法平衡快速执行的市场影响成本与缓慢执行的波动风险。在标准制定中，均值-方差最优交易策略是静态的：它们确实不根据交易过程中观察到的价格变动而修改执行速度。该论文表明，使用动态交易策略可以显着改善，并且对于大的初始头寸，改善更大。

该论文开发了一种技术，可以以任何所需的精度计算最佳动态策略。 资产价格过程是在具有任意数量级别的离散树上观察的。 该论文引入了一种新颖的动态规划技术，其中控制变量不仅是每个时间步交易的股票，而且是程序其余部分的最大预期成本； 价值函数是剩余程序的方差。 由此产生的自适应策略是“激进的价内策略”：当价格向有利于交易者的方向变动时，它们会加速执行，并花费部分交易收益来降低风险。

研究结论

通过动态规划原理的适当应用，该论文展示了如何针对 Almgren 和 Chriss [2000] 考虑的最优执行问题获得完全最优的自适应策略。 最优自适应策略比静态交易计划显着改善，对于大型投资组合来说改善更大。 正如 Almgren 和 Lorenz [2007] 所观察到的那样，这些适应性政策“在资金方面具有积极性”：如果价格朝着对您有利的方向变动，那么通过更快地交易该计划的其余部分，将这些收益用于市场影响成本。如果价格走势对你不利，然后通过更慢的交易来降低未来成本。这种将当前期间的利润与剩余时间内的预期利润相关联的情况也可以在多周期设置中的经典投资组合优化问题中观察到[Lorenz，2008 ，理查森，1989]。

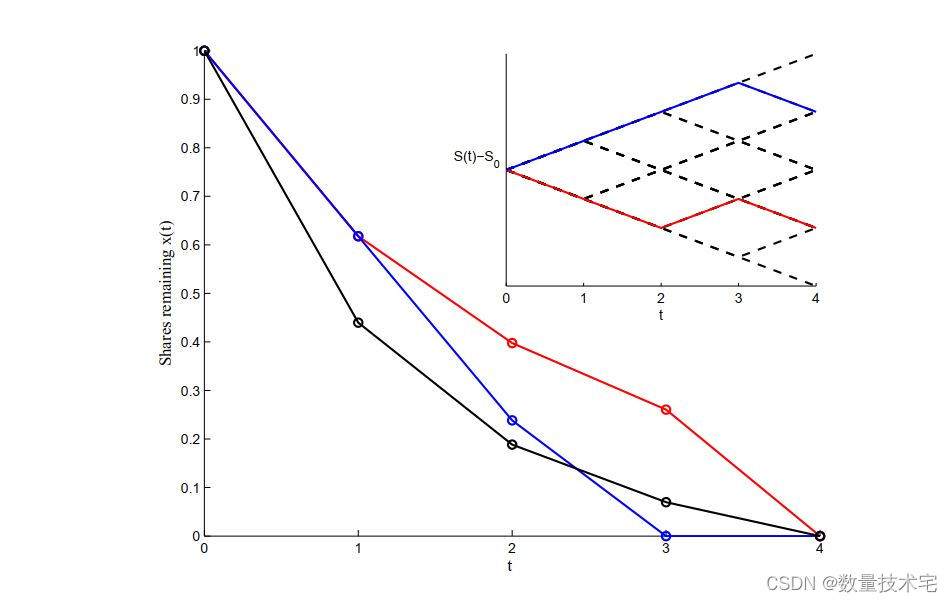
上图是 N = 4 个时间步长的最佳自适应交易，说明了二项式自适应模型。 蓝色轨迹对应于股价上涨路径，并且比红色轨迹（股价下跌路径）卖出得更快。 插图显示了二叉树上股票价格的示意图。 t = 1 时的 x1 对于所有自适应轨迹都是相同的，因为 x1 是在 t = 0 时确定的，没有可用信息。 仅从 t = 1 开始，自适应轨迹才会分裂。

HJB 优化交易执行方法

来自 Peter A. Forsyth 的《A Hamilton Jacobi Bellman Approach to Optimal Trade Execution》：

简介

最优交易执行问题是根据均值-方差权衡来制定的，如最初所见。 均值方差问题可以嵌入到线性二次 (LQ) 最优随机控制问题中，使用半拉格朗日方案来求解所得的非线性 Hamilton Jacobi Bellman (HJB) PDE。 该方法本质上独立于价格影响函数的形式。 提供强大的比较性质，该论文证明数值格式收敛于 HJB 偏微分方程的粘度解。 从有效交易前沿和交易策略方面给出了数值例子。 数值结果表明，在某些情况下，有许多不同的交易策略会产生几乎相同的有效边界。

研究结论

该论文根据等效的 LQ 问题制定了确定有效边界（以及相应的最优策略）的问题。 我们只需要求解单个非线性 HJB 方程（以及相关的线性 PDE）即可构建整个有效前沿。

HJB 方程使用半拉格朗日方法进行离散化。 假设HJB方程满足强比较性质，那么我们通过证明该格式是单调的、一致的和稳定的来证明收敛于粘度解。 请注意，在这种情况下，在粘度解意义上使用一致性是有用的 [8, 6]，因为半拉格朗日方法在计算域边界附近的点上不是经典一致的（对于任意网格大小）。

半拉格朗日离散化将基础随机过程模型与价格影响模型分开。 改变价格影响的特定模型相当于改变实现中的单个功能。 半拉格朗日方法也非常适合并行实现。

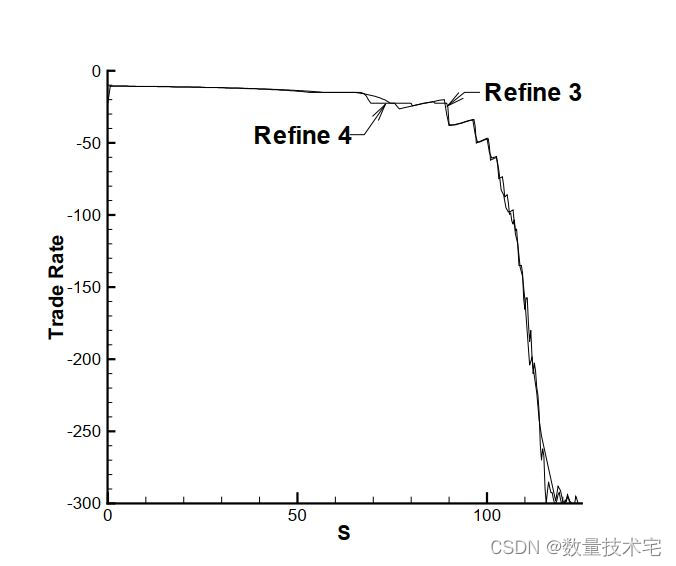
使用该论文中开发的方法计算的有效边界与直觉一致。 然而，最优交易率作为初始时资产价格的函数，对于大型资产价格表现出意想不到的锯齿图案。 对数值结果的详细分析表明，有许多策略给出了几乎相同的价值函数。 因此，最优策略（相对于有效边界）的数值问题似乎是不适定的。 请注意，这种不适定性似乎是预承诺均值方差目标函数的一个特定属性，如果使用替代目标函数（例如效用函数或均值二次变分），则不会看到这种不适定性。

然而，这种策略上的不恰当在实践中并没有特别令人不安。 最终的结果是，有许多策略基本上给出了相同的有效边界，这是实际重要性的衡量标准。 这也表明可以以不可预测的模式改变交易率，这可能有助于避免发出信号交易策略，但仍然可以获得平均方差有效的结果。

完整论文

本文原文英文文献，关注wx工中浩 数量技术宅 ，回复关键词：订单执行算法，即可获取。