DQN算法的全称为,Deep Q-Network,即在Q-learning算法的基础上引用深度神经网络来近似动作函数 Q ( s , a ) Q(s,a) Q(s,a) 。对于传统的Q-learning,当状态或动作数量特别大的时候,如处理一张图片,假设为 210 × 160 × 3 210×160×3 210×160×3,共有 25 6 ( 210 × 60 × 3 ) 256^{(210×60×3)} 256(210×60×3)种状态,难以存储,但可以使用参数化的函数 Q θ Q_{\theta} Qθ 来拟合这些数据,即DQN算法。同时DQN还引用了经验回放和目标网络,接下来将以此介绍。
CartPole 环境

在车杆环境中,通过移动小车,让小车上的杆保持垂直,如果杆的倾斜度数过大或者车子偏离初始位置的距离过大,或者坚持了一定的时间,则结束本轮训练。该智能体的状态是四维向量,每个状态是连续的,但其动作是离散的,动作的工作空间是2。
| 维度 | 意义 | 最小值 | 最大值 |
|---|---|---|---|
| 0 | 车的位置 | -2.4 | 2.4 |
| 1 | 车的速度 | -Inf | Inf |
| 2 | 杆的角度 | ~ -41.8° | ~ 41.8° |
| 3 | 杆尖端的速度 | -Inf | Inf |
| 标号 | 动作 |
|---|---|
| 0 | 向左移动小车 |
| 1 | 向右移动小车 |
深度网络
我们通过神经网络将输入向量
x
x
x映射到输出向量
y
y
y,通过下式表示:
y
=
f
θ
(
x
)
y=f_{\theta}(x)
y=fθ(x)
神经网络可以理解为是一个函数,输入输出都是向量,并且拥有可以学习的参数
θ
\theta
θ ,通过梯度下降等方法,使得神经网络能够逼近任意函数,当然可以用来近似动作价值函数:
y
⃗
=
Q
θ
(
s
⃗
,
a
⃗
)
\vec{y}=Q_{\theta}(\vec{s},\vec{a})
y=Qθ(s,a)
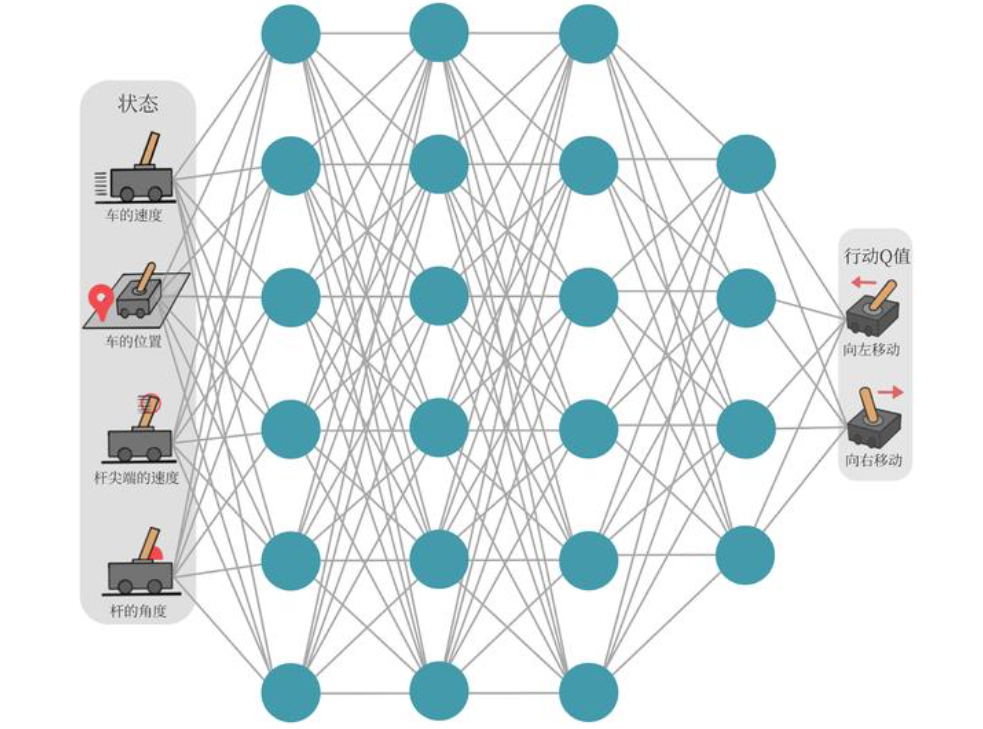
在本环境种,由于状态的每一维度的值都是连续的,无法使用表格记录,因此可以使用一个神经网络表示函数Q。当动作是连续(无限)时,神经网络的输入是状态s和动作a,输出一个标量,表示在状态s下采取动作a能获得的价值。若动作是离散(有限)的,除了采取动作连续情况下的做法,还可以只将状态s输入到神经忘了,输出每一个动作的Q值。
假设使用神经网络拟合w,则每一个状态s下所有可能动作a的Q值为 Q w ( s , a ) Q_w(s,a) Qw(s,a),我们称为Q网络:
我们在Q-learning种使用下面的方式更新:
Q
(
s
,
a
)
←
Q
(
s
,
a
)
+
α
[
r
+
γ
max
a
′
∈
A
Q
(
s
′
,
a
′
)
−
Q
(
s
,
a
)
]
Q(s,a)\leftarrow Q(s,a)+\alpha\left[r+\gamma\max_{a'\in\mathcal{A}}Q(s',a')-Q(s,a)\right]
Q(s,a)←Q(s,a)+α[r+γa′∈AmaxQ(s′,a′)−Q(s,a)]
即让
Q
(
s
,
a
)
Q(s,a)
Q(s,a)向
r
+
γ
max
a
′
∈
A
Q
(
s
′
,
a
′
)
r+\gamma\max_{a'\in\mathcal{A}}Q(s',a')
r+γmaxa′∈AQ(s′,a′)靠近,那么Q网络的损失函数为均方误差的形式:
ω
∗
=
arg
min
ω
1
2
N
∑
i
=
1
N
[
Q
ω
(
s
i
,
a
i
)
−
(
r
i
+
γ
max
a
′
Q
ω
(
s
i
′
,
a
′
)
)
]
2
\omega^*=\arg\min_{\omega}\frac{1}{2N}\sum_{i=1}^{N}\left[Q_\omega\left(s_i,a_i\right)-\left(r_i+\gamma\max_{a'}Q_\omega\left(s_i',a'\right)\right)\right]^2
ω∗=argωmin2N1i=1∑N[Qω(si,ai)−(ri+γa′maxQω(si′,a′))]2
经验回访
将Q-learning过程中,每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,之后在训练Q网络时,再从回访缓冲区中,随机采样若干数据进行训练。
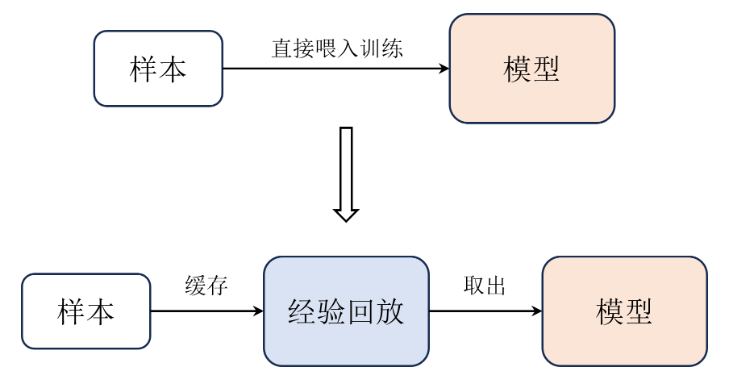
在一般的监督学习中,都是假定训练数据是独立同分布的,而在强化学习中,连续的采样、交互所得到的数据有很强的相关性,这一时刻的状态和上一时刻的状态有关,不满足独立假设。通过在回访缓冲区采样,可以打破样本之间的相关性。另外每一个样本可以使用多次,也适合深度学习。
目标网络
构建两个网络,一个是目标网络,一个是当前网络,二者结构相同,都用于近似Q值。在实践中每隔若干步才把每步更新的当前网络参数复制给目标网络,这样做的好处是保证训练的稳定,当训练的结果不好时,可以不同步当前网络的值,避免Q值的估计发散。
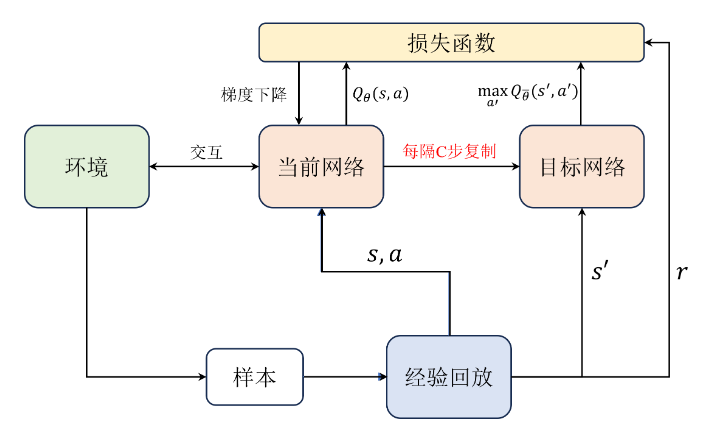
在计算期望时,使用目标网络来计算:
Q
期望
=
[
r
t
+
γ
max
a
′
Q
ω
ˉ
(
s
′
,
a
′
)
]
Q_\text{期望}=[r_t+\gamma\max_{a^{\prime}}Q_{\bar{\omega}}(s^{\prime},a^{\prime})]
Q期望=[rt+γa′maxQωˉ(s′,a′)]
具体流程如下所示:
- 使用随机的网络参数 ω \omega ω初始化初始化当前网络 Q ω ( s , a ) Q_{\omega}(s,a) Qω(s,a)
- 复制相同的参数初始化目标网络 ω ˉ ← ω \bar{\omega}\gets \omega ωˉ←ω
- 初始化经验回访池R
- for 序列
e
=
1
→
E
e=1\to E
e=1→E do
- 获取环境初始状态 s 1 s_1 s1
- for
时间步
t
=
1
→
T
时间步t=1\to T
时间步t=1→T do
- 根据当前网络 Q ω ( s , a ) Q_{\omega}(s,a) Qω(s,a) 以 ϵ − g r e e d y \epsilon -greedy ϵ−greedy策略选择动作 a t a_t at
- 执行动作 a t a_t at,获得回报 r t r_t rt,环境状态变为 s t + 1 s_{t+1} st+1
- 将 ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1)存储进回池R
- 若R中数据足够,则从R中采样N个数据 { ( s i , a i , r i , s i + 1 ) } i = 1 , … , N \{(s_i,a_i,r_i,s_{i+1})\}_{i=1,\ldots,N} {(si,ai,ri,si+1)}i=1,…,N
- 对每个数据,用目标网络计算 y = r i + γ max a Q ω ˉ ( s i + 1 , a ) y=r_i+\gamma\max_aQ_{\bar{\omega}}(s_{i+1},a) y=ri+γmaxaQωˉ(si+1,a)
- 最小化目标损失 L = 1 N ∑ i ( y i − Q ω ( s i , a i ) ) 2 L=\frac{1}{N}\sum_{i}(y_{i}-Q_{\omega}(s_{i},a_{i}))^{2} L=N1∑i(yi−Qω(si,ai))2,以更新当前网络 Q ω Q_{\omega} Qω
- 更新目标网络
- end for
- end for
import random
from typing import Any
import gymnasium as gym
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
# 首先定义经验回收池的类,包括加入数据、采样数据
class ReplayBuffer:
def __init__(self, capacity):
# 创建一个队列,先进先出
self.buffer=collections.deque(maxlen=capacity)
def add(self,state,action,reward,next_state,done):
# 加入数据
self.buffer.append((state,action,reward,next_state,done))
def sample(self,batch_size):
# 随机采样数据
mini_batch=random.sample(self.buffer,batch_size)
# zip(*)取mini_batch中的每个元素(即取列),并返回一个元组
state,action,reward,next_state,done=zip(*mini_batch)
return np.array(state), action, reward, np.array(next_state), done
def size(self):
return len(self.buffer)
# 定义一个只有一层隐藏层的Q网络
class Qnet(torch.nn.Module):
def __init__(self,state_dim,hidden_dim,action_dim):
super(Qnet,self).__init__()
# 定义一个全连接层,输入为state_dim维向量,输出为hidden_dim维向量
self.fc1=torch.nn.Linear(state_dim,hidden_dim)
# 定义一个全连接层,输入为hidden_dim维向量,输出为action_dim维向量
self.fc2=torch.nn.Linear(hidden_dim,action_dim)
def forward(self,state):
x = F.relu(self.fc1(state))
return self.fc2(x)
class DQN:
def __init__(self,state_dim,hidden_dim,action_dim,learning_rate,gamma,epsilon,target_update,device):
self.action_dim=action_dim
self.q_net=Qnet(state_dim,hidden_dim,action_dim).to(device)
# 目标网络
self.target_q_net=Qnet(state_dim,hidden_dim,action_dim).to(device)
# 使用Adam优化器
self.optimizer=torch.optim.Adam(self.q_net.parameters(),lr=learning_rate)
# 折扣因子
self.gamma=gamma
# 贪婪策略
self.epsilon=epsilon
# 目标网络更新频率
self.target_update=target_update
# 计数器
self.count=0
self.device=device
def take_action(self,state):
# 判断是否需要贪婪策略
if np.random.random()<self.epsilon:
action=np.random.randint(self.action_dim)
else:
state=torch.tensor([state],dtype=torch.float).to(self.device)
action=self.q_net(state).argmax().item()
return action
def update(self,transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
# Q值
q_values=self.q_net(states).gather(1,actions)
# 下一个状态的最大Q值
max_next_q_values=self.target_q_net(next_states).max(1)[0].view(-1, 1)
q_targets=rewards+self.gamma*max_next_q_values*(1-dones)
# 反向传播更新参数
dqn_loss=torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad()
dqn_loss.backward()
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(
self.q_net.state_dict()) # 更新目标网络
self.count += 1
lr = 2e-3
num_episodes = 500
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 10
buffer_size = 10000
minimal_size = 500
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
target_update, device)
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
state = env.reset()[0]
aa=state[0]
print(state)
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done,info, _ = env.step(action)
replay_buffer.add(state, action, reward, next_state, done)
state = next_state
episode_return += reward
# 当buffer数据的数量超过一定值后,才进行Q网络训练
if replay_buffer.size() > minimal_size:
b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
transition_dict = {
'states': b_s,
'actions': b_a,
'next_states': b_ns,
'rewards': b_r,
'dones': b_d
}
agent.update(transition_dict)
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)




![[linux]同步缓冲区数据到flash](https://img-blog.csdnimg.cn/direct/7e21dd9af1a049d5b288152ed0041fd0.png)