PCL中常用的高级采样方法

news2024/9/21 2:31:00

0. 简介

我们在使用PCL时候，常常不满足于常用的降采样方法，这个时候我们就想要借鉴一些比较经典的高级采样方法。这一讲我们将对常用的高级采样方法进行汇总，并进行整理，来方便读者完成使用

1. 基础下采样

1.1 点云随机下采样

点云下采样是对点云以一定的采样规则重新进行采样，目的是在保证点云整体几何特征不变的情况下，降低点云的密度，进而可以降低相关处理的数据量和算法复杂度。随机下采样顾名思义，随机下采样就似乎在原始点云中随机采样一定点数的点。这种方法最终得到的点云数量也是固定的。

	pcl::PointCloud<PointT>::Ptr cloud_sub(new pcl::PointCloud<PointT>);	//随机下采样点云
	pcl::RandomSample<PointT> rs;	//创建滤波器对象
	rs.setInputCloud(cloud);				//设置待滤波点云
	rs.setSample(20000);					//设置下采样点云的点数
	//rs.setSeed(1);						//设置随机函数种子点
	rs.filter(*cloud_sub);					//执行下采样滤波，保存滤波结果于cloud_sub

在这里插入图片描述

1.2 体素下采样

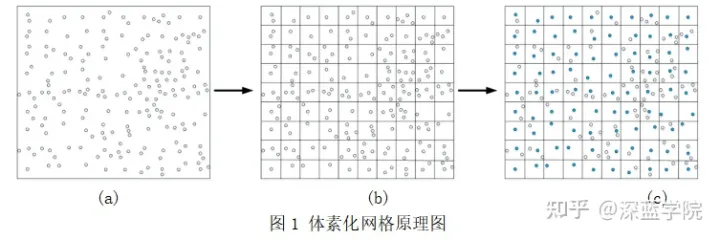
体素下采样的原理如图1所示，首先将点云空间进行网格化，也称体素化，即图1(b)，网格化后的每一个格子称为体素，在这些划分为一个个极小的格子中包含一些点，然后对这些点取平均或加权平均得到一个点，以此来替代原来网格中所有的点，即图1©中蓝色的点。显然，网格选取越大则采样之后的点云越少，处理速度变快，但会对原先点云过度模糊，网格选取越小，则作用相反。
在这里插入图片描述

 pcl::VoxelGrid<pcl::PointXYZ> sor;    //创建体素网格采样处理对象
 sor.setInputCloud(cloud);             //设置输入点云
 sor.setLeafSize(0.01f, 0.01f, 0.01f); //设置体素大小，单位：m
 sor.filter(*cloud_filtered);          //进行下采样

1.3 均匀采样

均匀采样的原理类似于体素化网格采样方法，同样是将点云空间进行划分，不过是以半径=r的球体，在当前球体所有点中选择距离球体中心最近的点替代所有点，注意，此时点的位置是不发生移动的。球体半径选取越大则采样之后的点云越少，处理速度变快，但会对原先点云过度模糊，网格选取越小，则作用相反。

pcl::UniformSampling<pcl::PointXYZ> form;   // 创建均匀采样对象
form.setInputCloud(cloud);                  //设置输入点云
form.setRadiusSearch(0.02f);                //设置半径大小,单位:m
form.filter(*after_cloud);                  //执行滤波处理

1.4 增采样

增采样的特点是可极大的增加点云数据，但由于内插点的不确定性会导致最后输出的结果不一定准确。

//创建增采样对象
pcl::MovingLeastSquares<pcl::PointXYZ,pcl::PointXYZ> filter;    
filter.setInputCloud(cloud);                     //设置输入点云
pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree;  //定义搜索方法
filter.setSearchMethod(kdtree);                  //设置搜索方法
filter.setSearchRadius(0.03);    //设置搜索邻域的半径为3cm  
//Upsampling 采样的方法还有 DISTINCT_CLOUD, RANDOM_UNIFORM_DENSITY
filter.setUpsamplingMethod(pcl::MovingLeastSquares<pcl::PointXYZ, pcl::PointXYZ>::SAMPLE_LOCAL_PLANE);     //对点云进行上采样
filter.setUpsamplingRadius(0.03);    //设置采样半径大小，3cm
filter.setUpsamplingStepSize(0.02);  //设置采样步长大小，2cm
filter.process(*after_cloud);      //执行采样操作

1.5 滑动最小二乘法采样

滑动最小二乘法采样的原理是将点云进行了滑动最小二乘法的映射，使得输出的点云更加平滑。

pcl::PointCloud<pcl::PointNormal>::Ptr smoothedCloud(new pcl::PointCloud<pcl::PointNormal>);   //定义法线
pcl::MovingLeastSquares<pcl::PointXYZ, pcl::PointNormal> filter;
pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree;  //定义搜索方法
filter.setInputCloud(cloud);    //设置输入点云
filter.setUpsamplingMethod();  //增加密度较小区域的密度对于holes的填补却无能为力，具体方法要结合参数使用
filter.setSearchRadius(10);// 用于拟合的K近邻半径。在这个半径里进行表面映射和曲面拟合。半径越小拟合后曲面的失真度越小，反之有可能出现过拟合的现象。
filter.setPolynomialFit(true);  //对于法线的估计是有多项式还是仅仅依靠切线。true为加多项式；false不加，速度较快
filter.setPolynomialFit(3);      // 拟合曲线的阶数
filter.setComputeNormals(true);  // 是否存储点云的法向量，true 为存储，false 不存储
filter.setSearchMethod(kdtree); //设置搜索方法
filter.process(*smoothedCloud); //处理点云并输出

2. 最远点采样(Farthest Point Sampling)

这个PCL代码目前已经集成到https://github.com/farthest_point_sampling.hpp。这里我们来单独看一下调用代码，这里可以看到PCL中支持直接调用farthest_sampling这个函数可以实现最远点采样。最远点采样(Farthest Point Sampling)是一种非常常用的采样算法，由于能够保证对样本的均匀采样，被广泛使用，像3D点云深度学习框架中的PointNet++对样本点进行FPS采样再聚类作为感受野，3D目标检测网络VoteNet对投票得到的散乱点进行FPS采样再进行聚类，6D位姿估计算法PVN3D中用于选择物体的8个特征点进行投票并计算位姿。FPS算法原理：

  1. 输入点云有N个点，从点云中选取一个点P0作为起始点，得到采样点集合S={P0}；
  2. 计算所有点到P0的距离，构成N维数组L，从中选择最大值对应的点作为P1，更新采样点集合S={P0，P1}；
  3. 计算所有点到P1的距离，对于每一个点Pi，其距离P1的距离如果小于L[i]，则更新L[i] = d(Pi, P1)，因此，数组L中存储的一直是每一个点到采样点集合S的最近距离；
  4. 选取L中最大值对应的点作为P2，更新采样点集合S={P0，P1，P2}；
  5. 重复2-4步，一直采样到N’个目标采样点为止。
  std::vector<pcl::PointCloud<pcl::PointXYZ>> input_point_clouds(1);
  std::vector<pcl::PointCloud<pcl::PointXYZ>> output_point_clouds;

  ASSERT_NE(pcl::io::loadPLYFile<pcl::PointXYZ>(STR(INPUT_POINT_CLOUD_PATH),
            input_point_clouds[0]), -1) << "Couldn't read file test point cloud file";
  farthest_sampling::samplePointCloudsCuda(input_point_clouds, output_point_clouds, 4096);
  boost::filesystem::path output_path = STR(OUTPUT_POINT_CLOUD_PATH);
  if (output_path.has_parent_path() && !boost::filesystem::exists(output_path.parent_path()))
  {
    boost::filesystem::create_directories(output_path.parent_path());
  }
  pcl::io::savePLYFile(STR(OUTPUT_POINT_CLOUD_PATH), output_point_clouds[0]);
  ASSERT_EQ(output_point_clouds[0].size(), 4096);

3. 法线空间采样

NormalSpaceSampling即：法线空间采样，它在法向量空间内均匀随机抽样，使所选点之间的法线分布尽可能大，结果表现为地物特征变化大的地方剩余点较多，变化小的地方剩余点稀少，可有效保持地物特征。实现方法如下：

  1. 首先计算每个点的K领域，然后计算点到领域点的法线夹角值，以此来近似达到曲率的效果并提高计算效率，因为曲率越大的地方，夹角值越大。

  2. 设置一个角度阈值，当点的领域夹角值大于阈值时被认为是特征明显的区域，其余区域为不明显区域。

  3. 对明显和不明显区域进行均匀采样，采样数分别为U*(1-V)和U*V,U是目标采样数，V是均匀采样性。

在这里插入图片描述

 // 创建基于邻域的法向估计类对象
 // // 基于omp并行加速，需配置开启OpenMP
 // pcl::NormalEstimationOMP<pcl::PointXYZ, pcl::Normal> ne; 
 // ne.setNumberOfThreads(10);
 pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> ne;
 // 创建一个空的kdtree对象，并把它传递给法线估计对象，
 // 用于创建基于输入点云数据的邻域搜索kdtree
 pcl::search::KdTree<pcl::PointXYZ>::Ptr \
             tree(new pcl::search::KdTree<pcl::PointXYZ>());
 // 传入待估计法线的点云数据，智能指针
 ne.setInputCloud(cloud_src);
 // 传入kdtree对象，智能指针
 ne.setSearchMethod(tree);
 // 设置邻域搜索半径
 ne.setRadiusSearch(0.1f);    // 设置半径时，要考虑到点云空间间距
 // // 也可以设置最近邻点个数
 // ne.setKSearch(25);
 // 设置视点源点，用于调整点云法向（指向视点），默认（0，0，0）
 ne.setViewPoint(0,0,0);
 // 计算法线数据
 ne.compute(*cloud_normals);

 // 通过concatenateFields函数将point和normal组合起来形成PointNormal点云数据
 pcl::PointCloud<pcl::PointNormal>::Ptr \
             cloud_with_normal(new pcl::PointCloud<pcl::PointNormal>());
 pcl::PointCloud<pcl::PointNormal>::Ptr \
     cloud_with_normal_sampled(new pcl::PointCloud<pcl::PointNormal>());
 pcl::concatenateFields(*cloud_src, *cloud_normals, *cloud_with_normal);

 // 创建法向空间采样（模板）类对象
 pcl::NormalSpaceSampling<pcl::PointNormal, pcl::Normal> nss;
 // 设置xyz三个法向空间的分类组数，此处设置为一致，根据具体场景可以调整
 const int kBinNum = 8;
 nss.setBins(kBinNum, kBinNum, kBinNum);
 // 如果传入的是有序点云，此处可以尝试设置为true
 nss.setKeepOrganized(false);
 // 设置随机种子，这样可以保证同样的输入可以得到同样的结果，便于debug分析
 nss.setSeed(200);   // random seed
 // 传入待采样的点云数据
 nss.setInputCloud(cloud_with_normal);
 // 传入用于采样分析的法线数据，需与传入点云数据一一对应
 nss.setNormals(cloud_normals);
 // 设置采样总数，即目标点云的总数据量
 const float kSampleRatio = 0.1f;
 nss.setSample(cloud_with_normal->size()*kSampleRatio);
 // 执行采样并带出采样结果
 nss.filter(*cloud_with_normal_sampled);

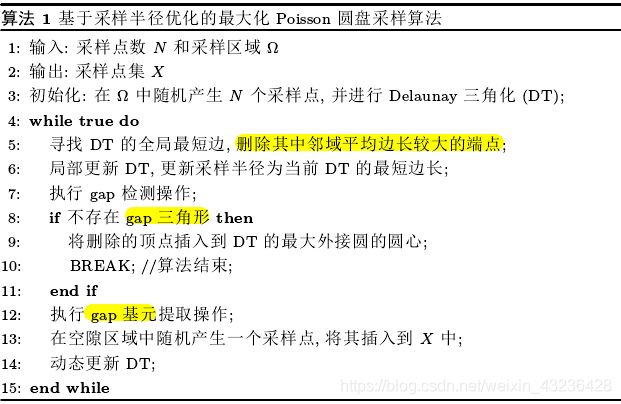
4. 泊松盘采样

泊松盘采样（possion disk sampling）的特点是任何两个点的距离都不会隔得太近。
比如下图，左边是随机生成的点，右边是泊松盘采样生成的点。
在这里插入图片描述
具体流程如下

  1. 设定好两个点之间最近的距离r，以及采样点所在空间的维度n，比如2维平面

  2. 在空间里生成足够多的网格，保证不接触的两个网格之间的点的距离大于r，并且网格数量足够多保证每个网格至多只需装一个采样点就能满足采样数量。为了最优化，一般取网格边长为r/\sqrt{n}。

  3. 随机生成一个点，再创建两个数组，第一个是处理数组，第二个是结果数组，即最终的输出数组。把这个点放进处理数组中和结果数组中。

  4. 如果处理数组非空，从中随机选择一个点，如下图的红点，并把这个点从处理数组中删除。如果处理数组是空的，直接输出结果数组并结束算法。

  5. 设定最小距离minr，比如r，最大距离maxr，比如2*r。以红点为中心生成一个圆环，如下图灰色圆环，在这个圆环中生成一个采样点，如下图蓝点。

在这里插入图片描述

…详情请参照古月居

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/138896.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

代码随想录拓展day6 N皇后

代码随想录拓展day6 N皇后

代码随想录拓展day6 N皇后 只有这一个内容。一刷的时候也没弄太明白&#xff0c;二刷的时候补上。还有部分内容来自牛客网左老师的算法课程。 总体思路不容易想明白&#xff0c;优化也有很大难度。这要是面试能碰上基本就是故意不给过了吧。 思路 首先来看一下皇后们的约束…
阅读更多...
Flink 容错恢复 2.0 2022 最新进展

Flink 容错恢复 2.0 2022 最新进展

摘要&#xff1a;本文整理自阿里云 Flink 存储引擎团队负责人&#xff0c;Apache Flink 引擎架构师 & PMC 梅源在 FFA 核心技术专场的分享。主要介绍在 2022 年度&#xff0c;Flink 容错 2.0 这个项目在社区和阿里云产品的进展&#xff0c;内容包括&#xff1a;Flink 容错恢…
阅读更多...
基于ssm的个人健康管理系统

基于ssm的个人健康管理系统

项目描述 临近学期结束&#xff0c;还是毕业设计&#xff0c;你还在做java程序网络编程&#xff0c;期末作业&#xff0c;老师的作业要求觉得大了吗?不知道毕业设计该怎么办?网页功能的数量是否太多?没有合适的类型或系统?等等。这里根据疫情当下&#xff0c;你想解决的问…
阅读更多...
简单理解光会产生折射的原因及折射定律的推导

简单理解光会产生折射的原因及折射定律的推导

已知 1、光是一种波&#xff1b; 2、光在不同介质中传播速度不同。 构建模型 如下图所示&#xff0c;光是中电磁波&#xff0c;以余弦波为例&#xff0c;取余弦波的极大值点为参考&#xff0c;建立一个平面波&#xff08;波前为一个平面&#xff09;。能明显的看出光的传播方…
阅读更多...
树形结构——二叉树

树形结构——二叉树

前言 前面的章节我们介绍了两种重要的数据结构&#xff0c;数组和链表&#xff0c;由于他们各自的特性使得他们的优缺点非常分明&#xff0c;在查询速度和插入速度上顾此失彼&#xff0c;不能兼顾&#xff0c;那么有没有一种数据结构可以同时高效的完成插入和查询操作呢&#x…
阅读更多...
专访 | 刘嘉松：开源，互惠且共赢

专访 | 刘嘉松：开源，互惠且共赢

本文整理自对 2022 开源之夏 OpenMLDB 社区贡献者刘嘉松同学的采访&#xff0c;欢迎大家关注~ OpenMLDB&#xff1a;可以先请你介绍一下你自己吗? 刘嘉松&#xff1a;我叫刘嘉松&#xff0c;是中南大学计科专业的一名本科生&#xff0c;目前大四&#xff0c;未来将继续在中南…
阅读更多...
Hello 2023 D. Boris and His Amazing Haircut

Hello 2023 D. Boris and His Amazing Haircut

原题链接&#xff1a;Problem - D - Codeforces 题意&#xff1a; 给定长度为 n 的数组 A &#xff0c;代表 Boris 现在的头发长度&#xff0c;和一个长度为 n 的数组 B &#xff0c;代表他希望的发型的头发长度。理发师手里有 m 把剪刀&#xff0c;每个都只能用一次&#xff…
阅读更多...
计算机硕士论文，盲审的老师都很严吗？ - 易智编译EaseEditing

计算机硕士论文，盲审的老师都很严吗？ - 易智编译EaseEditing

首先&#xff0c;学位论文必须论证严谨 对于一个结果的解读&#xff0c;先老老实实的把得到什么结果讲一遍&#xff0c;基于这个所得出的结论说一说&#xff0c;最后&#xff0c;来个非谓语的短句吹一吹重要性或提示意义。 这其实是有套路的一个句子写下来。但是&#xff0c;在…
阅读更多...
AC7811-ACMP模拟比较器

AC7811-ACMP模拟比较器

在无感的BLDC方波控制中&#xff0c;AC7811没办法再直接通过PWDT模块检测霍尔信号了。 所以需要先进行ACMP模块的初始化配置&#xff0c;使能ACMP模块正常工作后&#xff0c;ACMP会对输入的三相反电动势与电机中电电压进行轮询模拟&#xff0c;得到各相反电动势过零点&#xf…
阅读更多...
分享5款有趣但或许不那么实用的软件

分享5款有趣但或许不那么实用的软件

今天我想分享几个有趣但或许不那么实用的软件&#xff0c;各位喜欢的朋友可以自行下载呢。 1.软件音量设置——EarTrumpet 听音乐、看视频、玩游戏&#xff0c;在各应用切换过程中&#xff0c;你可能会频繁调整系统音量大小&#xff0c;以适应自己的耳朵。而 EarTrumpet 则可…
阅读更多...
AIGC：BAT、抖快的新掘金口？

AIGC：BAT、抖快的新掘金口？

配图来自Canva可画 AI辅助绘画估值超十万&#xff1f; 12月28日&#xff0c;山东人民出版社看中一位4岁女孩用百家号AI作画创作的AI绘本《超能外星战队》&#xff0c;认为该画价值超十万元且有出版意向。与此同时&#xff0c;“AI作画”像病毒般在各大短视频平台蔓延&#xf…
阅读更多...
年度盘点丨2022年，7大关键词彰显用友成长型企业数智力量

年度盘点丨2022年，7大关键词彰显用友成长型企业数智力量

导读&#xff1a;这一年&#xff0c;他们用卓越成绩证明自己&#xff0c;用产品创新回馈客户&#xff0c;用实力开启了中国成长型企业数智化产业的逆袭之路&#xff01; 2022年&#xff0c;企业级数智化产业经历了翻天覆地的变化。 曾经万家追捧的“舶来品”在成长型企业的主…
阅读更多...
项目管理中，如何对各种文件进行统一版本管理？

项目管理中，如何对各种文件进行统一版本管理？

不知道你在工作中是否也遇到过这样的问题&#xff1a;1、文件先存一个位置&#xff0c;等晚点再整理&#xff0c;结果过了一段时间&#xff0c;就变成了这样&#xff1a;2、想从电脑中找一份重要材料&#xff0c;要花费很长时间&#xff0c;有时查找一通&#xff0c;却一无所获…
阅读更多...
Docker中MySQL主从复制

Docker中MySQL主从复制

MySQL主从复制 主从搭建步骤 新建主服务器容器实例3307 docker run -p 3307:3306 --name mysql-master \ -v /mydata/mysql-master/log:/var/log/mysql \ -v /mydata/mysql-master/data:/var/lib/mysql \ -v /mydata/mysql-master/conf:/etc/mysql \ -e MYSQL_ROOT_PASSWORD…
阅读更多...
SAP年结账务调整过程中的业务改错处理心得

SAP年结账务调整过程中的业务改错处理心得

昨天遇到一个问题在这里分享一下。大家知道刚刚跨年&#xff0c;财务还在做一些后续调整。在业财一体化的系统中&#xff0c;这种调整往往涉及到两个方向&#xff0c;财务端去调&#xff0c;还是业务端去调。但大家要了解一个前提。即然需要做调整&#xff0c;肯定是业务端出错…
阅读更多...
IPC（IP CAMERA）

IPC（IP CAMERA）

IPC是IP Camera的缩写词&#xff0c;IP是网际协定&#xff0c;Camera是照相机、摄影机&#xff0c;IP Camera顾名思义就是网路摄像机&#xff0c;它是一种由传统摄像机与网路技术结合所产生的新一代摄像机。 注&#xff1a;NVR&#xff0c;全称Network Video Recorder&#xff…
阅读更多...
有哪些设备管理软件值得推荐？

有哪些设备管理软件值得推荐？

有哪些设备管理软件值得推荐&#xff1f; 别滑了&#xff0c; 翻遍全网&#xff0c;好用的设备管理软件都给你整理好了&#xff0c;白嫖的好事可千万别错过。 要知道好用的设备管理软件&#xff0c;可是能为企业持续、稳定、快速发展&#xff0c;及提高经济效益发挥重要作用。…
阅读更多...
机器学习实战教程（九）：支持向量机实战篇

机器学习实战教程（九）：支持向量机实战篇

一、前言 上篇文章讲解的是线性SVM的推导过程以及简化版SMO算法的代码实现。本篇文章将讲解SMO算法的优化方法以及非线性SVM。 本文出现的所有代码&#xff0c;均可在我的github上下载&#xff0c;欢迎Follow、Star&#xff1a;点击查看 二、SMO算法优化 在几百个点组成的小规…
阅读更多...
数据的存储

数据的存储

数据的存储 文章目录数据的存储一、数据类型二、整形在内存中的存储2.1 原码、反码、补码2.2 大小端介绍2.3几个经典关于内存存储的例子三、浮点型在内存中的存储3.1 一个令你惊呆的例子3.2 浮点数存储规则一、数据类型 整形家族&#xff1a; char&#xff1a; unsigned char&a…
阅读更多...
redhat9---MySQL8练习

redhat9---MySQL8练习

目录 1、显示所有职工的基本信息。 2、查询所有职工所属部门的部门号&#xff0c;不显示重复的部门号。 3、求出所有职工的人数。 4、列出最高工资和最低工资。 5、列出职工的平均工资和总工资。 6、创建一个只有职工号、姓名和参加工作的新表&#xff0c;名为工作日…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023