【蓝桥杯日记】第二篇——递归问题的处理

news2025/1/11 9:10:57

前言

大家好呀！我是大雄！一个菜鸡！接下来的几个月和大家分享一下自己在备战蓝桥中遇到的一些问题。感谢大家提出好的思路以及好的学习方法。我提前在这里谢谢大家了，也希望大家能够在蓝桥中取得好的名次。我们一起共勉！加油！！！

本周主要练习的题目是递归，因为每天也就给练习算法的时间大约是一个多小时，所以整体进度比较缓慢，只希望自己能够赎回报名费，当然也要像其他算法大佬学习！欢迎各位算法大佬对大雄提出的意见和建议，我一定会认真听取的。接下来我们进入正题，递归。

递归，当学习完成基础语法后，进入算法界可能是我们遇到的第一个问题。当我们看着简单的递归代码却想不清楚代码具体逻辑的时候，推荐大家去看一部电影——盗梦空间。最开始我在学习完递归之后一头雾水，当时老师就推荐去看这部电影。看完整部电影之后好像还是似懂非懂。

递归

递归：及“函数的自己调用自己”,这个可能就是我们的第一印象吧。

官方的回答是：递归是指一种或多种简单的基本情况定义的一类对象或方法，并规定其他所有情况都能被还原为其基本情况。

递归解决的问题

在现实生活中，有很多问题比较复杂，直接解决这个问题比较困难，但是这些问题可以被分解为n个较小规模与原结构相似的子问题，通过解决这些相对简单的子问题，得到子问题的解，然后将子问题的解合并，从而得到原问题的解。(上边的文字多读几遍)

上边虽然说的简单对子问题的拆分，如何拆分？

递归的三要素

终止条件：当递归函数符合这个规则是，不在进行自己调用自己。从而避免死递归。
继续推进：每一次递归，都要将子问题进行划分，朝着终止条件进行，否则无法结束递归。
设计法则: 也就是根据递归的规律，写出递归代码。

递归设计的经验:

1）找重复（子问题划分）

2）找重复中的变化量——>参数

3）找参数变化趋势——>递归出口

递归的练习（由浅入深）

1.循环改为递归

eg:计算1-100之内累加和？

这应该是学完for循环的练习题目，接下来我们先按照for循环的形式，然后更具三要素逐步转化为递归的形式。

 //for循环
int count=0;
        for (int i = 1; i <=100 ; i++) {
            count+=i;
        }
        System.out.println(count);

//递归
static int fun3(int n) {
    if (n == 1)
        return 1;
    return n+fun3(n-1);
}

分析:

找重复：n+(n-1),求n-1的累加就是原问题的重复(规模更小)——子问题
找变化：每次都是n+(n-1)
设置出口：每次都是n-1,会朝着1这个方向下去，直到等于1然后递归结束。

我是这样理解的：fun3是张三，最近张三落难了，手头只有10万，急需100万。于是靠着自己“法外狂徒”的名号，向小弟借钱。张三小弟自己把自己的钱拿出来然后在想自己的小弟借钱，然后把自己的钱和借自己小弟的钱给张三。直到凑够100万张三就不凑了！

2.斐波那契

斐波那契数列是一串递增的整数，其中每一项都是前两项的和。这个数列从0和1开始，其前几项为：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …。以此类推，第n项的值可以表示为F(n)。

斐波那契数列的性质：

F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) 对于所有 n > 1

递推的做法:

static void fun4(int n) {
//        求斐波那契的第n项
//       0 1(第一项) 1 2 3 5
    int f1 = 1, f2 = 1, fn = -1;
    if (n == 1) {
        System.out.println(f1);
    } else if (n == 2) {
        System.out.println(f2);
    } else {
        for (int i = 3; i <= n; i++) {
//          后一项=前一项+前第二项
            fn = f1 + f2;
            f1 = f2;
            f2 = fn;
        }
        System.out.println(fn);
    }
}

递归的做法：

//    斐波那契数列
    static  int Fibonacci(int n){
        if(n==1||n==2){
            return 1;
        }
        return Fibonacci(n-1)+Fibonacci(n-2);
    }

分析(递归):

找重复：求n项需要求n-1项和n-1项，并将n-1项和n-2项加起来，如果实在想不明白可以把n当前3,然后将n-1就是2和n-2就是1,在进行调用自生就是1+1等于2。递归结束。
找变化：n-1项+n-1项
设置出口：斐波那契的第一项和第二项都等于1

3.汉诺塔问题

汉诺塔问题是一个古老而著名的数学问题，源于印度的一个古老传说。这个问题涉及三个柱子，通常标记为A、B和C。这三个柱子上分别堆叠着若干数量的圆盘，圆盘的大小不同，且按照从小到大的顺序从下到上堆叠在A柱子上。
汉诺塔问题的目标是在遵循一定规则的前提下，将所有的圆盘从一个柱子移动到另一个柱子。具体规则如下：

每次只能移动一个圆盘。
在移动过程中，任何时候都不能将一个较大的圆盘放在一个较小的圆盘上面。
可以利用第三个柱子（B柱子）作为辅助柱子，即可以在B柱子上暂时放置圆盘。
对于任何一个具体的步骤，实际上都需要进行三次移动：

将上面的n-1个盘子从起始柱子（如A）移到另一个柱子（如B）；
将最大的盘子从起始柱子移到目标柱子（如C）；
最后，将n-1个盘子从临时柱子（如B）移到目标柱子（如C）

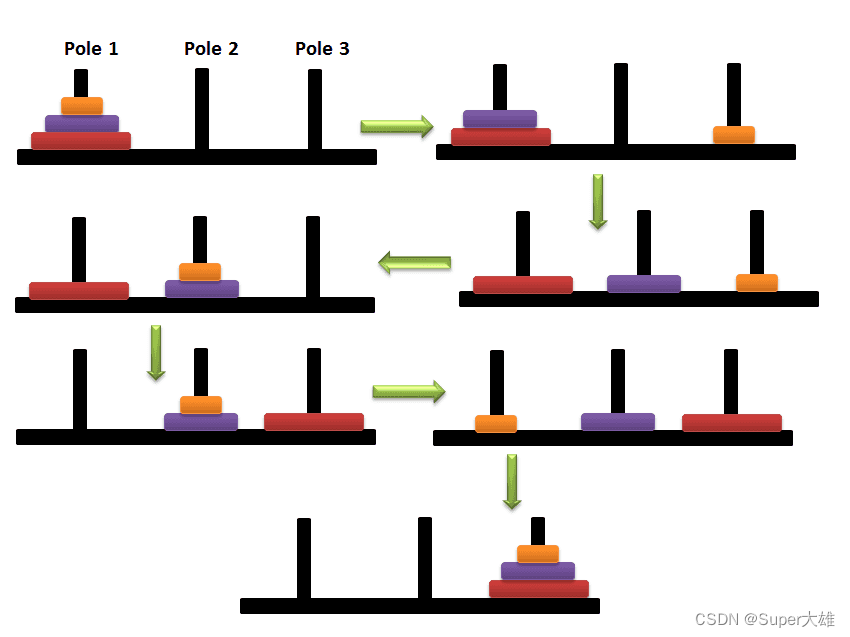
个人分析：

开始所有的盘子都在A柱子，从上到下(从小到大)及1—n-1看做一个整体，最后一个最大的盘子看做一个整体，现将1—n-1移动到C柱，B柱作为辅助的柱子。
将A柱最大的盘子移动到B柱
将C柱的盘子移动到B柱，借助A柱作为辅助的柱子。

static void hanoiTower(int N,String from,String to,String help){
//N为盘子的个数，按照从小到大排序
//    from 原始柱子 to 到达的柱子 help 辅助的柱子
    if(N==1){
//        移动最后一个盘子
        System.out.println("move"+N+"from"+from+"to"+to);
        return;
    }
    //把前n-1个盘子移动到辅助空间
    hanoiTower(N-1,from,help,to);
//    N移动到target
    System.out.println("move"+N+"from"+from+"to"+to);
//    让前n-1个盘子所在的辅助空间移动到源空间
    hanoiTower(N-1,help,to,from);
}