高校教务系统密码加密逻辑及JS逆向

本文将介绍高校教务系统的密码加密逻辑以及使用JavaScript进行逆向分析的过程。通过本文,你将了解到密码加密的基本概念、常用加密算法以及如何通过逆向分析来破解密码。
本文仅供交流学习,勿用于非法用途。
一、密码加密基本概念
密码加密是一种保护信息安全的技术手段,它通过将明文(原始信息)转换为密文(加密后的信息),以防止未经授权的访问和篡改。常见的密码加密算法有MD5、SHA-1、SHA-256等。
1.1 加密过程
加密过程通常包括以下步骤:
- 密钥扩展:将密钥扩展为多个轮值,每个轮值都与明文的一部分有关。
- 初始轮值生成:将扩展后的密钥与轮常数进行某种运算,生成第一轮加密的密文。
- 多轮迭代:对密文进行多轮迭代操作,每轮操作都包括非线性函数、模运算和轮常数的变换。
- 最终密文:经过多轮迭代后,得到最终的密文。
1.2 解密过程
解密过程与加密过程相反,通过反向操作来恢复原始明文。通常需要知道加密时使用的密钥和算法。
二、高校教务系统密码加密逻辑分析
2.1 抓包
我们首先打开教务系统的登录页面,我们可以看到,只有学号和密码,有的高校会有验证码,或者有的高校是错误一次密码,会验证验证码。
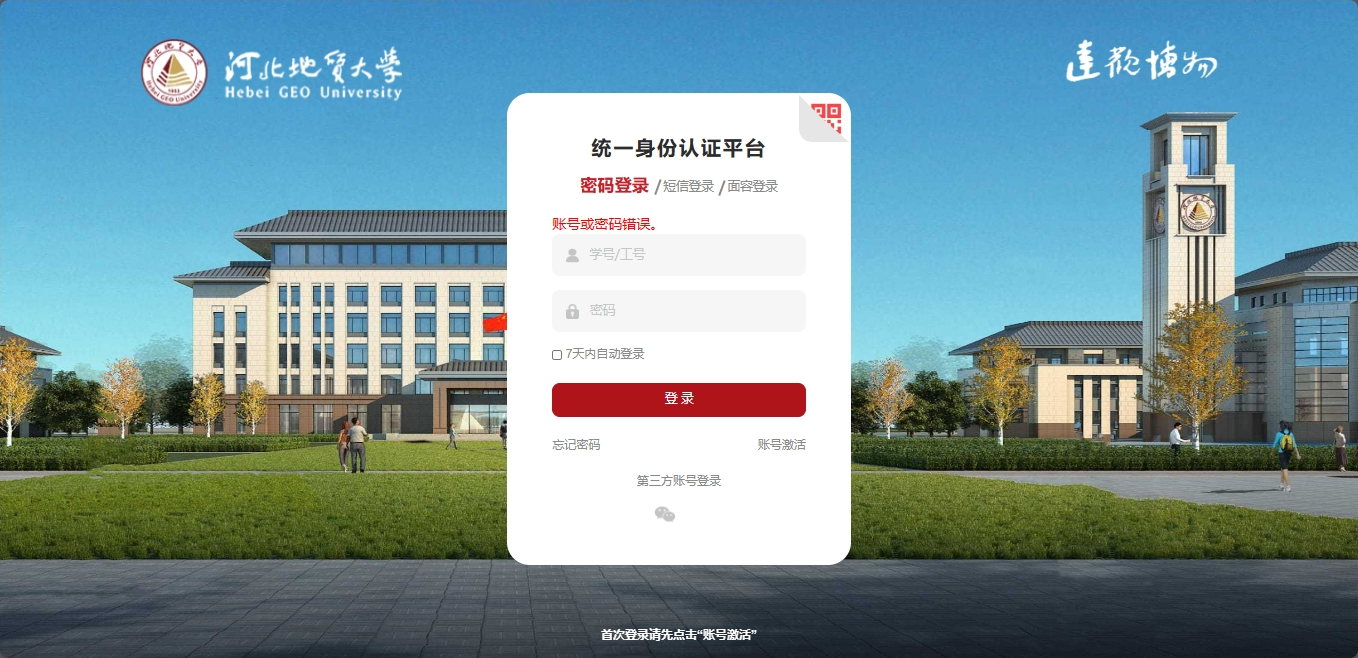
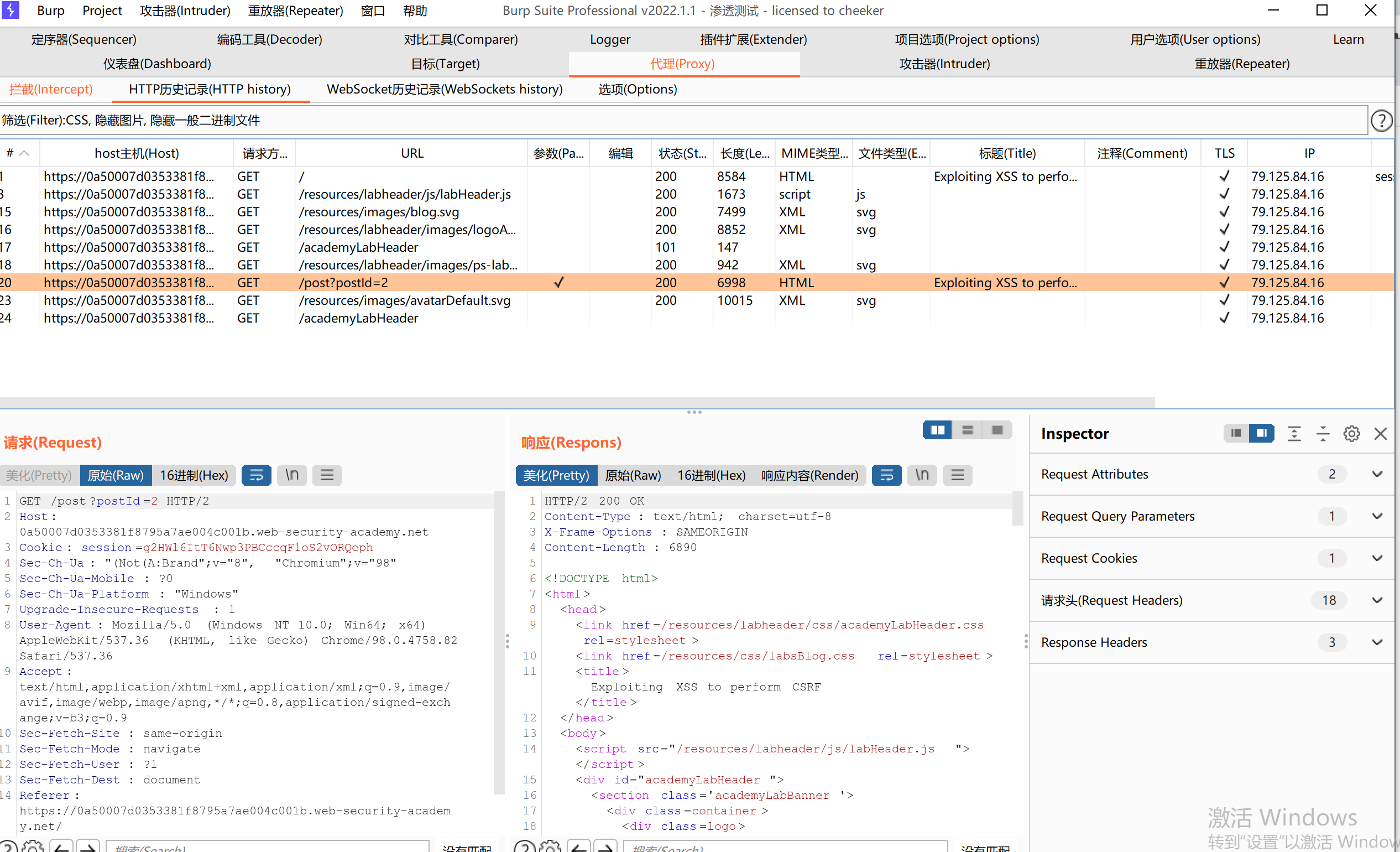
我们打开开发者工具,尝试登录抓包,网页会返回这样的数据接口。
2.2 分析加密参数
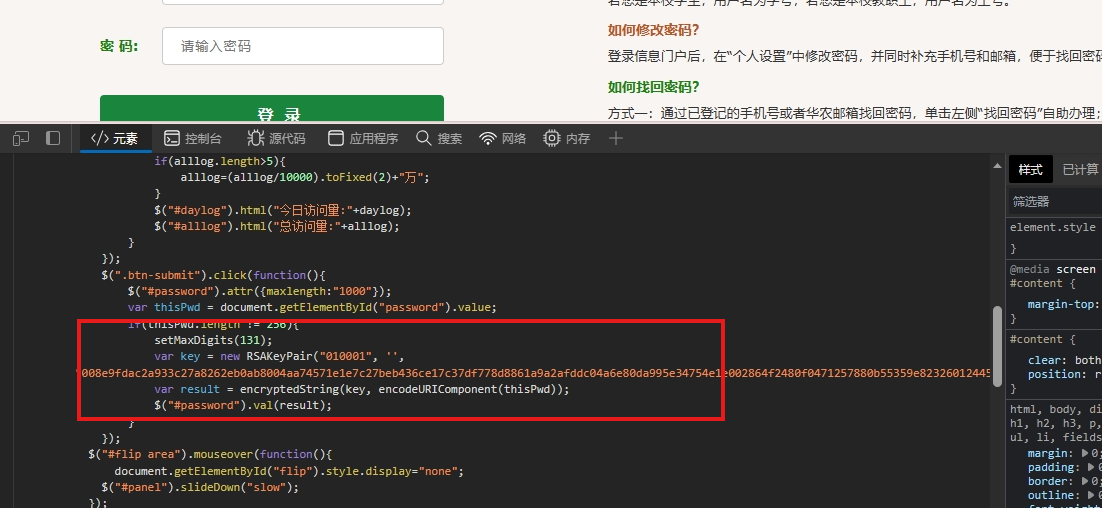
我们接下来,就是来分析这个密码是怎么加密的。我们全局搜索password。定位到加密的位置。
我们搜索之后,会发现找不到,我们重新刷新一下网页,我们先不用登录,为什么搜不到,因为网页结构发生了变化。

我们搜索password,发现上面有一行字符串,我们仔细一看,就是加密方法。接下来,就是扣代码了。
三、JS逆向分析方法
逆向分析是指从已知的加密文本或程序中还原出原始信息的过程。在本例中,我们将使用JavaScript编写一个简单的逆向分析工具,用于逆向高校教务系统的密码。
环境使用
- python 3.9
- pycharm
- node
我们全局搜索encryptedString,我们接下来就是扣这个函数吗,看缺什么补什么。这个就比较简单了,直接扣下来就可以了。
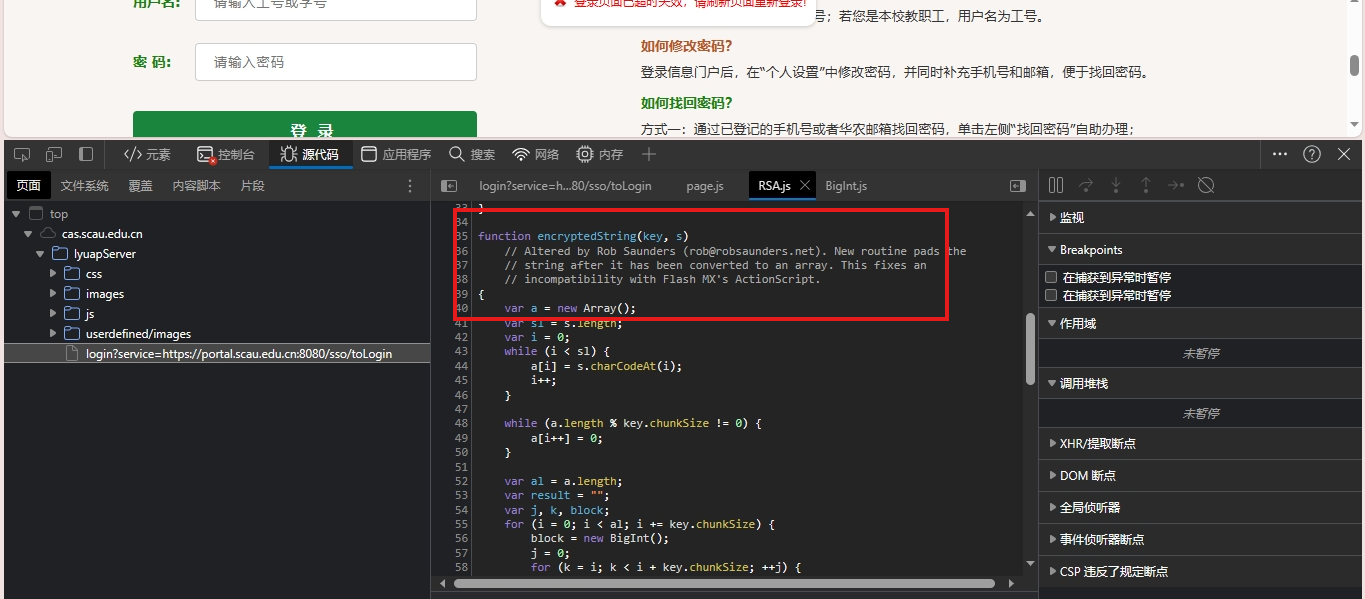
代码实现
我们先把这些代码扣下来,运行看看缺什么补什么。
var biRadixBits = 16;
var bitsPerDigit = biRadixBits;
var biRadix = 1 << 16; // = 2^16 = 65536
var biHalfRadix = biRadix >>> 1;
var biRadixSquared = biRadix * biRadix;
var maxDigitVal = biRadix - 1;
var maxDigits;
var ZERO_ARRAY;
var bigZero, bigOne;
function setMaxDigits(value)
{
maxDigits = value;
ZERO_ARRAY = new Array(maxDigits);
for (var iza = 0; iza < ZERO_ARRAY.length; iza++) ZERO_ARRAY[iza] = 0;
bigZero = new BigInt();
bigOne = new BigInt();
bigOne.digits[0] = 1;
}
setMaxDigits(20);
var dpl10 = 15;
// lr10 = 10 ^ dpl10
var lr10 = biFromNumber(1000000000000000);
function BigInt(flag)
{
if (typeof flag == "boolean" && flag == true) {
this.digits = null;
}
else {
this.digits = ZERO_ARRAY.slice(0);
}
this.isNeg = false;
}
function biCopy(bi)
{
var result = new BigInt(true);
result.digits = bi.digits.slice(0);
result.isNeg = bi.isNeg;
return result;
}
function biFromNumber(i)
{
var result = new BigInt();
result.isNeg = i < 0;
i = Math.abs(i);
var j = 0;
while (i > 0) {
result.digits[j++] = i & maxDigitVal;
i = Math.floor(i / biRadix);
}
return result;
}
function reverseStr(s)
{
var result = "";
for (var i = s.length - 1; i > -1; --i) {
result += s.charAt(i);
}
return result;
}
var hexatrigesimalToChar = new Array(
'0', '1', '2', '3', '4', '5', '6', '7', '8', '9',
'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j',
'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't',
'u', 'v', 'w', 'x', 'y', 'z'
);
function biToString(x, radix)
// 2 <= radix <= 36
{
var b = new BigInt();
b.digits[0] = radix;
var qr = biDivideModulo(x, b);
var result = hexatrigesimalToChar[qr[1].digits[0]];
while (biCompare(qr[0], bigZero) == 1) {
qr = biDivideModulo(qr[0], b);
digit = qr[1].digits[0];
result += hexatrigesimalToChar[qr[1].digits[0]];
}
return (x.isNeg ? "-" : "") + reverseStr(result);
}
var hexToChar = new Array('0', '1', '2', '3', '4', '5', '6', '7', '8', '9',
'a', 'b', 'c', 'd', 'e', 'f');
function digitToHex(n)
{
var mask = 0xf;
var result = "";
for (i = 0; i < 4; ++i) {
result += hexToChar[n & mask];
n >>>= 4;
}
return reverseStr(result);
}
function biToHex(x)
{
var result = "";
var n = biHighIndex(x);
for (var i = biHighIndex(x); i > -1; --i) {
result += digitToHex(x.digits[i]);
}
return result;
}
function charToHex(c)
{
var ZERO = 48;
var NINE = ZERO + 9;
var littleA = 97;
var littleZ = littleA + 25;
var bigA = 65;
var bigZ = 65 + 25;
var result;
if (c >= ZERO && c <= NINE) {
result = c - ZERO;
} else if (c >= bigA && c <= bigZ) {
result = 10 + c - bigA;
} else if (c >= littleA && c <= littleZ) {
result = 10 + c - littleA;
} else {
result = 0;
}
return result;
}
function hexToDigit(s)
{
var result = 0;
var sl = Math.min(s.length, 4);
for (var i = 0; i < sl; ++i) {
result <<= 4;
result |= charToHex(s.charCodeAt(i))
}
return result;
}
function biFromHex(s)
{
var result = new BigInt();
var sl = s.length;
for (var i = sl, j = 0; i > 0; i -= 4, ++j) {
result.digits[j] = hexToDigit(s.substr(Math.max(i - 4, 0), Math.min(i, 4)));
}
return result;
}
function biAdd(x, y)
{
var result;
if (x.isNeg != y.isNeg) {
y.isNeg = !y.isNeg;
result = biSubtract(x, y);
y.isNeg = !y.isNeg;
}
else {
result = new BigInt();
var c = 0;
var n;
for (var i = 0; i < x.digits.length; ++i) {
n = x.digits[i] + y.digits[i] + c;
result.digits[i] = n % biRadix;
c = Number(n >= biRadix);
}
result.isNeg = x.isNeg;
}
return result;
}
function biSubtract(x, y)
{
var result;
if (x.isNeg != y.isNeg) {
y.isNeg = !y.isNeg;
result = biAdd(x, y);
y.isNeg = !y.isNeg;
} else {
result = new BigInt();
var n, c;
c = 0;
for (var i = 0; i < x.digits.length; ++i) {
n = x.digits[i] - y.digits[i] + c;
result.digits[i] = n % biRadix;
// Stupid non-conforming modulus operation.
if (result.digits[i] < 0) result.digits[i] += biRadix;
c = 0 - Number(n < 0);
}
// Fix up the negative sign, if any.
if (c == -1) {
c = 0;
for (var i = 0; i < x.digits.length; ++i) {
n = 0 - result.digits[i] + c;
result.digits[i] = n % biRadix;
// Stupid non-conforming modulus operation.
if (result.digits[i] < 0) result.digits[i] += biRadix;
c = 0 - Number(n < 0);
}
// Result is opposite sign of arguments.
result.isNeg = !x.isNeg;
} else {
// Result is same sign.
result.isNeg = x.isNeg;
}
}
return result;
}
function biHighIndex(x)
{
var result = x.digits.length - 1;
while (result > 0 && x.digits[result] == 0) --result;
return result;
}
function biNumBits(x)
{
var n = biHighIndex(x);
var d = x.digits[n];
var m = (n + 1) * bitsPerDigit;
var result;
for (result = m; result > m - bitsPerDigit; --result) {
if ((d & 0x8000) != 0) break;
d <<= 1;
}
return result;
}
function biMultiply(x, y)
{
var result = new BigInt();
var c;
var n = biHighIndex(x);
var t = biHighIndex(y);
var u, uv, k;
for (var i = 0; i <= t; ++i) {
c = 0;
k = i;
for (j = 0; j <= n; ++j, ++k) {
uv = result.digits[k] + x.digits[j] * y.digits[i] + c;
result.digits[k] = uv & maxDigitVal;
c = uv >>> biRadixBits;
//c = Math.floor(uv / biRadix);
}
result.digits[i + n + 1] = c;
}
// Someone give me a logical xor, please.
result.isNeg = x.isNeg != y.isNeg;
return result;
}
function biMultiplyDigit(x, y)
{
var n, c, uv;
result = new BigInt();
n = biHighIndex(x);
c = 0;
for (var j = 0; j <= n; ++j) {
uv = result.digits[j] + x.digits[j] * y + c;
result.digits[j] = uv & maxDigitVal;
c = uv >>> biRadixBits;
//c = Math.floor(uv / biRadix);
}
result.digits[1 + n] = c;
return result;
}
function arrayCopy(src, srcStart, dest, destStart, n)
{
var m = Math.min(srcStart + n, src.length);
for (var i = srcStart, j = destStart; i < m; ++i, ++j) {
dest[j] = src[i];
}
}
var highBitMasks = new Array(0x0000, 0x8000, 0xC000, 0xE000, 0xF000, 0xF800,
0xFC00, 0xFE00, 0xFF00, 0xFF80, 0xFFC0, 0xFFE0,
0xFFF0, 0xFFF8, 0xFFFC, 0xFFFE, 0xFFFF);
function biShiftLeft(x, n)
{
var digitCount = Math.floor(n / bitsPerDigit);
var result = new BigInt();
arrayCopy(x.digits, 0, result.digits, digitCount,
result.digits.length - digitCount);
var bits = n % bitsPerDigit;
var rightBits = bitsPerDigit - bits;
for (var i = result.digits.length - 1, i1 = i - 1; i > 0; --i, --i1) {
result.digits[i] = ((result.digits[i] << bits) & maxDigitVal) |
((result.digits[i1] & highBitMasks[bits]) >>>
(rightBits));
}
result.digits[0] = ((result.digits[i] << bits) & maxDigitVal);
result.isNeg = x.isNeg;
return result;
}
var lowBitMasks = new Array(0x0000, 0x0001, 0x0003, 0x0007, 0x000F, 0x001F,
0x003F, 0x007F, 0x00FF, 0x01FF, 0x03FF, 0x07FF,
0x0FFF, 0x1FFF, 0x3FFF, 0x7FFF, 0xFFFF);
function biShiftRight(x, n)
{
var digitCount = Math.floor(n / bitsPerDigit);
var result = new BigInt();
arrayCopy(x.digits, digitCount, result.digits, 0,
x.digits.length - digitCount);
var bits = n % bitsPerDigit;
var leftBits = bitsPerDigit - bits;
for (var i = 0, i1 = i + 1; i < result.digits.length - 1; ++i, ++i1) {
result.digits[i] = (result.digits[i] >>> bits) |
((result.digits[i1] & lowBitMasks[bits]) << leftBits);
}
result.digits[result.digits.length - 1] >>>= bits;
result.isNeg = x.isNeg;
return result;
}
function biMultiplyByRadixPower(x, n)
{
var result = new BigInt();
arrayCopy(x.digits, 0, result.digits, n, result.digits.length - n);
return result;
}
function biDivideByRadixPower(x, n)
{
var result = new BigInt();
arrayCopy(x.digits, n, result.digits, 0, result.digits.length - n);
return result;
}
function biModuloByRadixPower(x, n)
{
var result = new BigInt();
arrayCopy(x.digits, 0, result.digits, 0, n);
return result;
}
function biCompare(x, y)
{
if (x.isNeg != y.isNeg) {
return 1 - 2 * Number(x.isNeg);
}
for (var i = x.digits.length - 1; i >= 0; --i) {
if (x.digits[i] != y.digits[i]) {
if (x.isNeg) {
return 1 - 2 * Number(x.digits[i] > y.digits[i]);
} else {
return 1 - 2 * Number(x.digits[i] < y.digits[i]);
}
}
}
return 0;
}
function biDivideModulo(x, y)
{
var nb = biNumBits(x);
var tb = biNumBits(y);
var origYIsNeg = y.isNeg;
var q, r;
if (nb < tb) {
// |x| < |y|
if (x.isNeg) {
q = biCopy(bigOne);
q.isNeg = !y.isNeg;
x.isNeg = false;
y.isNeg = false;
r = biSubtract(y, x);
// Restore signs, 'cause they're references.
x.isNeg = true;
y.isNeg = origYIsNeg;
} else {
q = new BigInt();
r = biCopy(x);
}
return new Array(q, r);
}
q = new BigInt();
r = x;
// Normalize Y.
var t = Math.ceil(tb / bitsPerDigit) - 1;
var lambda = 0;
while (y.digits[t] < biHalfRadix) {
y = biShiftLeft(y, 1);
++lambda;
++tb;
t = Math.ceil(tb / bitsPerDigit) - 1;
}
// Shift r over to keep the quotient constant. We'll shift the
// remainder back at the end.
r = biShiftLeft(r, lambda);
nb += lambda; // Update the bit count for x.
var n = Math.ceil(nb / bitsPerDigit) - 1;
var b = biMultiplyByRadixPower(y, n - t);
while (biCompare(r, b) != -1) {
++q.digits[n - t];
r = biSubtract(r, b);
}
for (var i = n; i > t; --i) {
var ri = (i >= r.digits.length) ? 0 : r.digits[i];
var ri1 = (i - 1 >= r.digits.length) ? 0 : r.digits[i - 1];
var ri2 = (i - 2 >= r.digits.length) ? 0 : r.digits[i - 2];
var yt = (t >= y.digits.length) ? 0 : y.digits[t];
var yt1 = (t - 1 >= y.digits.length) ? 0 : y.digits[t - 1];
if (ri == yt) {
q.digits[i - t - 1] = maxDigitVal;
} else {
q.digits[i - t - 1] = Math.floor((ri * biRadix + ri1) / yt);
}
var c1 = q.digits[i - t - 1] * ((yt * biRadix) + yt1);
var c2 = (ri * biRadixSquared) + ((ri1 * biRadix) + ri2);
while (c1 > c2) {
--q.digits[i - t - 1];
c1 = q.digits[i - t - 1] * ((yt * biRadix) | yt1);
c2 = (ri * biRadix * biRadix) + ((ri1 * biRadix) + ri2);
}
b = biMultiplyByRadixPower(y, i - t - 1);
r = biSubtract(r, biMultiplyDigit(b, q.digits[i - t - 1]));
if (r.isNeg) {
r = biAdd(r, b);
--q.digits[i - t - 1];
}
}
r = biShiftRight(r, lambda);
// Fiddle with the signs and stuff to make sure that 0 <= r < y.
q.isNeg = x.isNeg != origYIsNeg;
if (x.isNeg) {
if (origYIsNeg) {
q = biAdd(q, bigOne);
} else {
q = biSubtract(q, bigOne);
}
y = biShiftRight(y, lambda);
r = biSubtract(y, r);
}
// Check for the unbelievably stupid degenerate case of r == -0.
if (r.digits[0] == 0 && biHighIndex(r) == 0) r.isNeg = false;
return new Array(q, r);
}
function biDivide(x, y)
{
return biDivideModulo(x, y)[0];
}
function RSAKeyPair(encryptionExponent, decryptionExponent, modulus)
{
this.e = biFromHex(encryptionExponent);
this.d = biFromHex(decryptionExponent);
this.m = biFromHex(modulus);
// We can do two bytes per digit, so
// chunkSize = 2 * (number of digits in modulus - 1).
// Since biHighIndex returns the high index, not the number of digits, 1 has
// already been subtracted.
this.chunkSize = 2 * biHighIndex(this.m);
this.radix = 16;
this.barrett = new BarrettMu(this.m);
}
function twoDigit(n)
{
return (n < 10 ? "0" : "") + String(n);
}
function encryptedString(key, s)
// Altered by Rob Saunders (rob@robsaunders.net). New routine pads the
// string after it has been converted to an array. This fixes an
// incompatibility with Flash MX's ActionScript.
{
var a = new Array();
var sl = s.length;
var i = 0;
while (i < sl) {
a[i] = s.charCodeAt(i);
i++;
}
while (a.length % key.chunkSize != 0) {
a[i++] = 0;
}
var al = a.length;
var result = "";
var j, k, block;
for (i = 0; i < al; i += key.chunkSize) {
block = new BigInt();
j = 0;
for (k = i; k < i + key.chunkSize; ++j) {
block.digits[j] = a[k++];
block.digits[j] += a[k++] << 8;
}
var crypt = key.barrett.powMod(block, key.e);
var text = key.radix == 16 ? biToHex(crypt) : biToString(crypt, key.radix);
result += text + " ";
}
return result.substring(0, result.length - 1); // Remove last space.
}
function BarrettMu(m)
{
this.modulus = biCopy(m);
this.k = biHighIndex(this.modulus) + 1;
var b2k = new BigInt();
b2k.digits[2 * this.k] = 1; // b2k = b^(2k)
this.mu = biDivide(b2k, this.modulus);
this.bkplus1 = new BigInt();
this.bkplus1.digits[this.k + 1] = 1; // bkplus1 = b^(k+1)
this.modulo = BarrettMu_modulo;
this.multiplyMod = BarrettMu_multiplyMod;
this.powMod = BarrettMu_powMod;
}
function BarrettMu_modulo(x)
{
var q1 = biDivideByRadixPower(x, this.k - 1);
var q2 = biMultiply(q1, this.mu);
var q3 = biDivideByRadixPower(q2, this.k + 1);
var r1 = biModuloByRadixPower(x, this.k + 1);
var r2term = biMultiply(q3, this.modulus);
var r2 = biModuloByRadixPower(r2term, this.k + 1);
var r = biSubtract(r1, r2);
if (r.isNeg) {
r = biAdd(r, this.bkplus1);
}
var rgtem = biCompare(r, this.modulus) >= 0;
while (rgtem) {
r = biSubtract(r, this.modulus);
rgtem = biCompare(r, this.modulus) >= 0;
}
return r;
}
function BarrettMu_multiplyMod(x, y)
{
/*
x = this.modulo(x);
y = this.modulo(y);
*/
var xy = biMultiply(x, y);
return this.modulo(xy);
}
function BarrettMu_powMod(x, y)
{
var result = new BigInt();
result.digits[0] = 1;
var a = x;
var k = y;
while (true) {
if ((k.digits[0] & 1) != 0) result = this.multiplyMod(result, a);
k = biShiftRight(k, 1);
if (k.digits[0] == 0 && biHighIndex(k) == 0) break;
a = this.multiplyMod(a, a);
}
return result;
}
var thisPwd = '1234';
setMaxDigits(131);
var key = new RSAKeyPair("010001", '', "008aed7e057fe8f14c73550b0e6467b023616ddc8fa91846d2613cdb7f7621e3cada4cd5d812d627af6b87727ade4e26d26208b7326815941492b2204c3167ab2d53df1e3a2c9153bdb7c8c2e968df97a5e7e01cc410f92c4c2c2fba529b3ee988ebc1fca99ff5119e036d732c368acf8beba01aa2fdafa45b21e4de4928d0d403");
var result = encryptedString(key, encodeURIComponent(thisPwd));
console.log(result)
我这里直接把代码给大家,大家感兴趣可以先尝试直接去写,可以和我写的做比较。
实现效果
8036bbd59644d65b1c7f264d4fc4970b32acb4964c5aedbeed5698a506dfed8cc8b08e150876b202975e5fad8a813236ec7e8105dae5311ad33056e8bb6895abb97d390d7bc9a8b5faf45e3c615fa774b96ea6ffdba1c3cd2289a6410ad2cf52452f26f3b94cba129b5c09b051b6bde71d1d777a28d6b07add45c9edace4b2d3
我们可以发现,这个结果和网页的结果一样的,说明我们逆向成功了,这里的加密稍微有点复杂,一个函数去扣就可以了。
四、总结
本文介绍了高校教务系统的密码加密逻辑以及使用JavaScript进行逆向分析的方法。通过学习这些知识,你可以更好地理解密码加密技术的原理,并掌握一定的逆向分析技巧。请注意,逆向分析可能涉及到法律问题,请在合法范围内进行研究和实践。
五、累计更新
争取到到底早日更新30所高校,大家可以在评论区留言。前期更的可能会多一点,有的学校教务系统都没有加密,我这里就不写了,还有,部分学校的教务系统已经和我之前写的是一样的,我也不重复赘述了。
往期作品可以查看专栏👇👇👇
全国高校教务系统登录页面JS分析_爱吃饼干的小白鼠的博客-CSDN博客









![[笔记]深度学习入门 基于Python的理论与实现(一)](https://img-blog.csdnimg.cn/direct/a2b26ac12c8f402fa94282dfd5b03d82.png)