核心结论

1：LLM模型的性能主要与计算量C，模型参数量N和数据大小D三者相关，而与模型的具体结构 (层数/深度/宽度) 基本无关。三者满足:  C ≈ 6ND

2. 为了提升模型性能，模型参数量N和数据大小D需要同步放大，但模型和数据分别放大的比例还存在争议。

核心公式：本部分来自参考2.

• 第一项是指无法通过增加模型规模来减少的损失，可以认为是数据自身的熵（例如数据中的噪音）
• 第二项是指能通过增加计算量来减少的损失，可以认为是模型拟合的分布与实际分布之间的差。

根据公式，增大 (例如计算量C)，模型整体loss下降，模型性能提升；伴随 (例如计算量C) 趋向于无穷大，模型能拟合数据的真实分布，让第二项逼近0，整体趋向于

结论验证

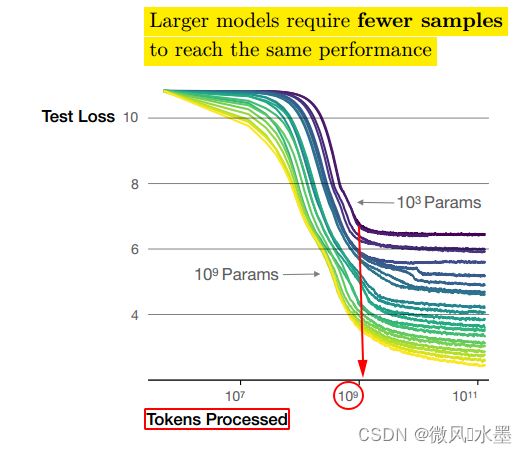
从图上可以看出：

1：当模型的参数量 N 为时（图中紫色的线），在 Token 数量达到 后（图中红色的圈），模型基本收敛，继续增加训练的 Token 数量，纵轴的Test Loss 并没有明显下降。

2：如果此时，增加模型的参数量N：->。 纵轴的Test Loss：从6.x->3.x。可以看出：提升模型参数量带来的收益更大。

测试一下：你对 scale law 的理解程度：基于上图，当模型的参数量 N 为时（图中紫色的线），模型收敛需要的算力C，以及耗时呢？

先看实验答案：下图红色箭头指向位置，也就是图中紫色线的拐点。

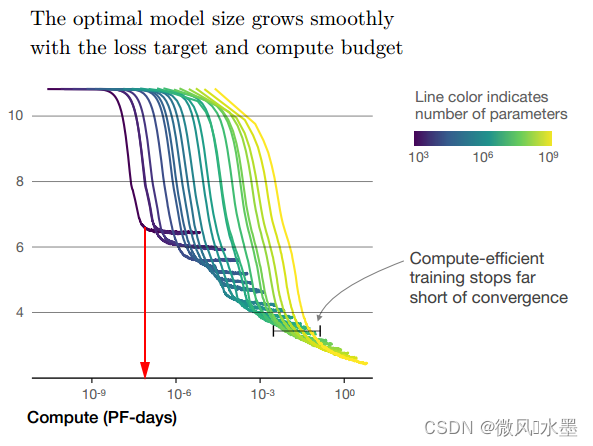
如果没做实验，收敛算力和收敛耗时该怎么推算呢？

Tips：

PF-days: 如果每秒钟可进行1015次运算，就是1 peta flops，那么一天的运算就是1015×24×3600=8.64×1019，这个算力消耗被称为1个petaflop/s-day。

再看个例子：

下图是Baichuan-2技术报告中的Scaling Law曲线。基于10M到3B的模型在1T数据上训练的性能，可预测出最后7B模型和13B模型在2.6T数据上的性能。

 在1T的数据上，训练的10M-3B的模型，是怎么推算训练7B/13B需要2.6T数据呢？

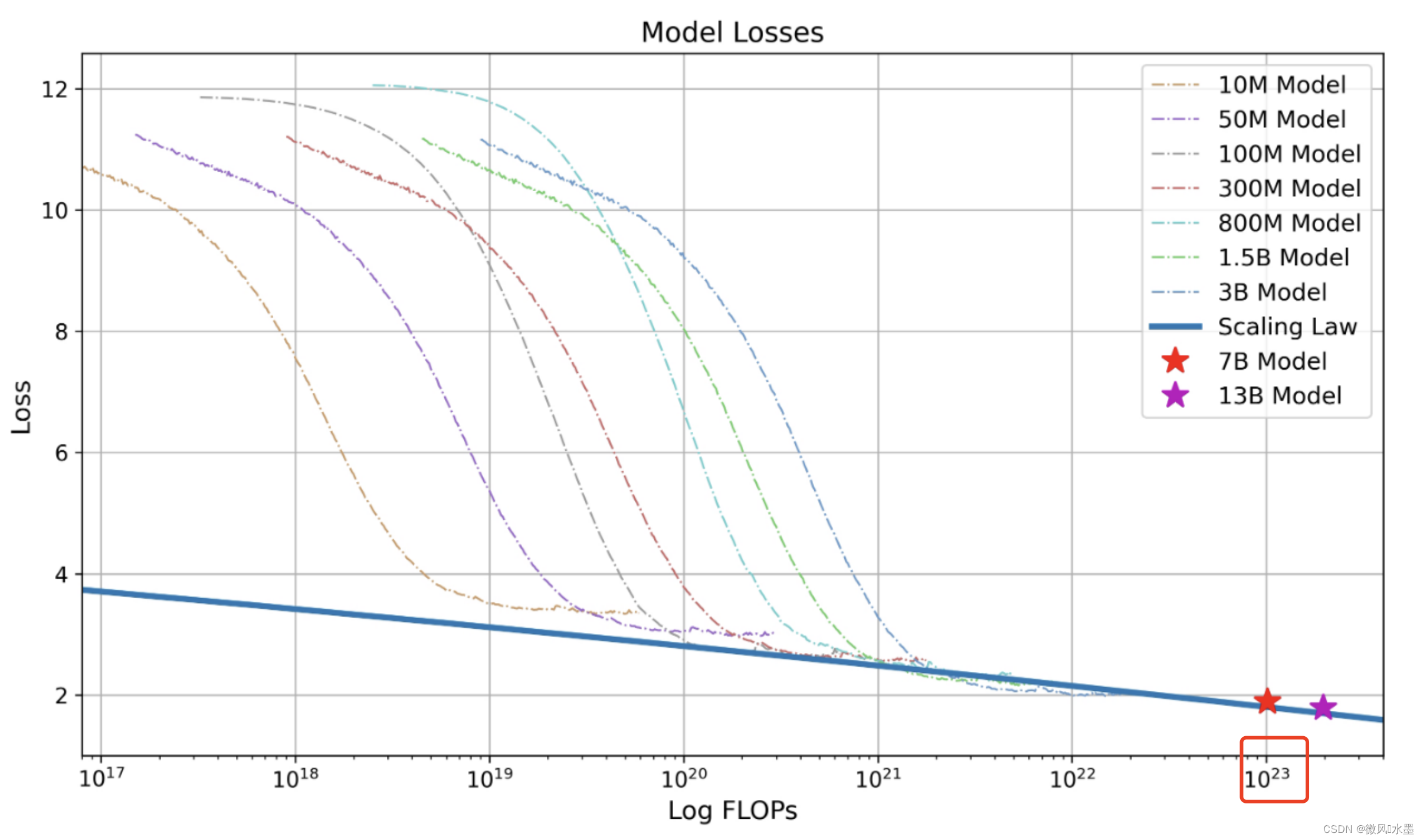
2.38T 是理论数值，与 2.6T基本一致了。

参考

1：介绍一些Scaling Laws - 知乎

2：解析大模型中的Scaling Law - 知乎