文章目录
- 一、积分分离PID
- 1.1 积分分离PID算法基本思想
- 1.2 积分分离PID算法实现步骤
- 1.3 积分分离PID算法
- 1.4 积分分离PID算法实现
- 1.5 积分分离PID算法仿真实例
- 1.6 积分分离PID算法的优缺点
- 二、抗积分饱和PID
- 2.1 积分饱和现象
- 2.2 抗积分饱和算法
- 2.3 抗积分饱和算法实现
- 2.4 抗积分饱和算法仿真实例
一、积分分离PID
1.1 积分分离PID算法基本思想
在普通PID控制中,引入
积分环节的目的主要是为了消除静差,提高控制精度。但在过程的启动、结束或大幅度增减设定时,短时间内系统输出有很大的偏差,会造成PID运算的积分积累,致使控制量超过执行机构可能允许的最大动作范围对应的极限控制量,引起系统较大的振荡,这在生产中是绝对不允许的。
- 积分分离控制基本思路是:当被控量与设定值偏差较大时,取消积分作用,以免由于积分作用使系统稳定性降低,超调量增大;当被控量接近给定量时,引入积分控制,以便消除静差,提高控制精度。
1.2 积分分离PID算法实现步骤
- 根据实际情况,人为设定阈值 ε > 0 ε>0 ε>0;
- 当 ∣ e ( k ) ∣ > ε ∣e (k)∣> ε ∣e(k)∣>ε时,采用PD控制,可避免产生过大的超调,又使系统有较快的响应;
- 当 ∣ e ( k ) ∣ ≤ ε ∣e (k)∣≤ ε ∣e(k)∣≤ε时,采用PID控制,以保证系统的控制精度。
1.3 积分分离PID算法

式中,T 为采样时间,β 项为积分项的开关系数.

由上述表述及公式我们可以知道,积分分离算法的效果其实与𝜺值的选取有较大的关系,所以𝜺值的选取实际上是实现的难点。𝜺 过大则达不到积分分离的效果,而𝜺 过小则难以进入积分区。
1.4 积分分离PID算法实现
根据积分分离式PID控制算法程序流程图如下图所示,由右图我们可以知道,与普通的PID算法的区别,只是判断偏差的大小,偏差大时为PD算法,偏差小时为PID算法。

1.5 积分分离PID算法仿真实例
设被控对象为一个延迟对象:
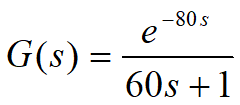
采样时间为20s,延迟时间为4个采样时间,即80s,被控对象离散化为:
![]()

- 积分分离PID算法的说明:为保证引入积分作用后系统的稳定性不变,在输入积分作用时,比例系数Kp可进行相应变化。再次强调,ε 值应根据具体对象及要求而定,若 ε 过大,则达不到积分分离的目的;ε 过小,则会导致无法进入积分区,而如果只进行PD控制,会使控制出现余差。
1.6 积分分离PID算法的优缺点
- 积分分离式PID通过引入判断误差大小条件,决定是否使用积分项。
- 优点:判定误差比较大的时候,取消积分项的,使用PD或者P控制,没有I的控制,这样,超调量和调节时间都会同时减少。当误差比较小的时候,引入积分项,消除静态误差。
- 缺点:需要经验来确定判断误差的大小,在什么时候使用积分分离比较合适,也就是误差多大的时候取消积分。
二、抗积分饱和PID
2.1 积分饱和现象
- 所谓积分饱和现象是指若系统存在一个方向的偏差,PID控制器的输出由于积分作用的不断累加而加大,从而导致执行机构达到极限位置Xmax(例如阀门开度达到最大)。
- 如下图所示,若控制器输出u(k)继续增大,阀门开度不可能再增大,此时就称计算机输出控制量超出了正常运行范围而进入了饱和区。一旦系统出现反向偏差,u(k)逐渐从饱和区退出。进入饱和区越深则退出饱和区所需要的时间越长。在这段时间内,执行机构仍停留在极限位置而不能随偏差反向立即做出相应的改变,这时系统就像
失去控制一样,造成控制性能恶化。这种现象称为积分饱和现象或积分失控现象。

2.2 抗积分饱和算法
作为防止积分饱和的方法之一就是抗积分饱和法。该方法的思路是在计算u(k)时,首先判断上一时刻的控制量 u(k-1) 是否己超出限制范围:
- 若 𝒖(𝒌−𝟏)>𝒖_𝒎𝒂𝒙 ,则只累加负偏差;
- 若 𝒖(𝒌−𝟏)<𝒖_𝒎𝒊𝒏,则只累加正偏差。
这种算法可以避免控制量长时间停留在饱和区。
2.3 抗积分饱和算法实现
抗积分饱和的思想很简单,在控制器输出的最大最小值附近限制积分的累积情况,以防止在恢复时没有响应。根据前面的分析我们可以得到如右图所示的算法流程图。

2.4 抗积分饱和算法仿真实例
设被控制对象为:

采样时间为1ms,取指令信号Rin(k)=30,M=1,采用抗积分饱和算法进行离散系统阶跃响应。

结论:由仿真结果可以看出,采用抗积分饱和PID方法,可以避免控制量长时间停留在饱和区,防止系统产生超调。
本节完