Leetcode2707. 字符串中的额外字符

news2024/11/15 9:21:37

Every day a Leetcode

题目来源：2707. 字符串中的额外字符

解法1：动态规划

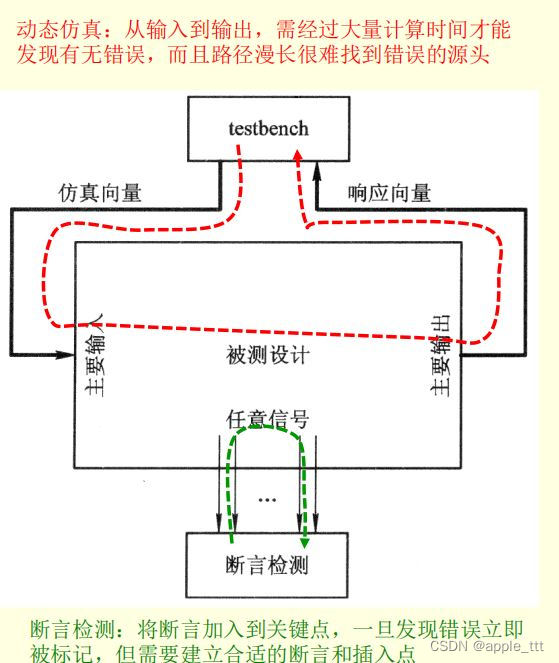
题目要求将字符串 s 分割成若干个互不重叠的子字符串（以下简称为子串），同时要求每个子串都必须在 dictionary 中出现。一些额外的字符可能不属于任何子串，而题目要求最小化这些额外字符的数量。

设 n 是 s 的长度，现在有两种基本的分割方案：

把 s 的最后一个字符 s[i−1] 当做是额外字符，那么问题转为长度为 i−1 的子问题。
找到一个 j 使得 s 的后缀 s[j…i−1] 构成的子串在 dictionary，那么问题转为长度为 j−1 的子问题。

设 dp[i] 是 s[0,…,i] 中额外字符的最小值。

状态转移：

把 s[i-1] 当成额外字符，dp[i] = dp[i - 1] + 1。
遍历所有的 j(j∈[0,i−1])，如果子字符串 s[j…i−1] 存在于 dictionary 中，那么 dp[i] = min(dp[i], dp[j])。

初始状态 d[0]=0，最终答案为 d[n]。

查找子串 s[j…i−1] 是否存在于 dictionary 可以使用哈希表。

代码：

/*
 * @lc app=leetcode.cn id=2707 lang=cpp
 *
 * [2707] 字符串中的额外字符
 */

// @lc code=start
class Solution
{
public:
    int minExtraChar(string s, vector<string> &dictionary)
    {
        int n = s.length();
        // dp[i] 是 s[0,...,i] 中额外字符的最小值
        vector<int> dp(n + 1, INT_MAX);
        // 初始化
        dp[0] = 0;

        // 建哈希表
        unordered_map<string, int> hash;
        for (string &dic : dictionary)
            hash[dic]++;

        // 状态转移
        for (int i = 1; i <= n; i++)
        {
            // 将 s[i-1] 视为额外的字符，额外字符数 +1
            dp[i] = dp[i - 1] + 1;
            for (int j = i - 1; j >= 0; j--)
            {
                string temp = s.substr(j, i - j);
                if (hash.count(temp))
                {
                    // 状态转移方程
                    dp[i] = min(dp[i], dp[j]);
                }
            }
        }
        return dp[n];
    }
};
// @lc code=end

结果：

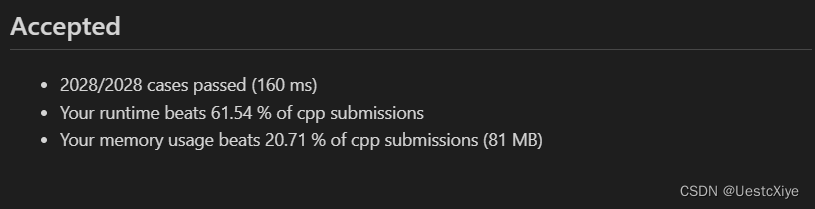
在这里插入图片描述

复杂度分析：

在这里插入图片描述

解法2：字典树优化

注意到，方法一查找某个子串是否在 dictionary 时效率很低，假设我们已经查找了子串 s[j+1…i−1]，接下来又要查找子串 s[j…i−1]，而后者只比前者多了一个字符 s[j]，却要花 O(n) 的时间重复查找。

我们可以使用字典树来优化这一过程。

由于我们总是查找 s 的后缀是否存在，因此需要将 dictionary 中的字符串翻转后插入字典树。在找到字典树上表示后缀 s[j+1…i−1] 的节点后，只需要 O(1) 的时间来判断表示后缀 s[j…i−1] 的节点是否存在。因此，转移过程的总时间复杂度为 O(n)，动态规划整体求解的时间复杂度降低为 O(n²)。

代码：

// 字典树优化

class Trie
{
private:
    vector<Trie *> children;
    bool isEnd;

public:
    Trie() : children(26), isEnd(false) {}

    void insert(string word)
    {
        Trie *node = this;
        for (char ch : word)
        {
            ch -= 'a';
            if (node->children[ch] == nullptr)
            {
                node->children[ch] = new Trie();
            }
            node = node->children[ch];
        }
        node->isEnd = true;
    }

    bool track(Trie *&node, char ch)
    {
        if (node == nullptr || node->children[ch - 'a'] == nullptr)
        {
            node = nullptr;
            return false;
        }
        node = node->children[ch - 'a'];
        return node->isEnd;
    }
};

class Solution
{
public:
    int minExtraChar(string s, vector<string> &dictionary)
    {
        int n = s.size();
        vector<int> d(n + 1, INT_MAX);
        Trie trie;
        for (auto s : dictionary)
        {
            reverse(s.begin(), s.end());
            trie.insert(s);
        }
        d[0] = 0;
        for (int i = 1; i <= n; i++)
        {
            d[i] = d[i - 1] + 1;
            Trie *node = &trie;
            for (int j = i - 1; j >= 0; j--)
            {
                if (trie.track(node, s[j]))
                {
                    d[i] = min(d[i], d[j]);
                }
            }
        }
        return d[n];
    }
};