1.计数排序思想

计数排序，顾名思义就是计算数据的个数

计数排序又称非比较排序

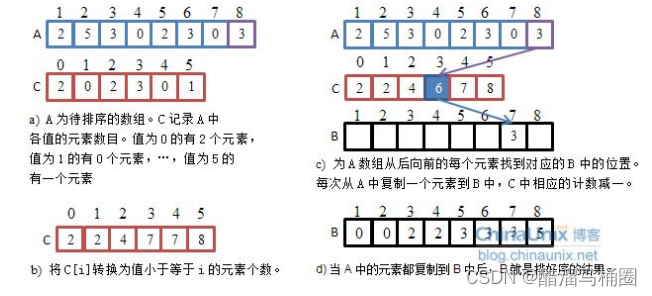
思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。 操作步骤：

1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中

计数排序的特性总结：

1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(MAX(N,范围))
3. 空间复杂度：O(范围)

2.计数排序过程

首先统计每个数据出现了多少次

假设有这么一个数组，下面的数组就是统计数据个数的

如果1出现，则对1位置++，如果3出现，则对3位置++，即

这里的代码核心稍微比较抽象，是在统计a数组中数据个数

接下来的操作是这样，对比count数组，0出现了0次，那就是0个0，1出现了3次，那就是3个1，其余同理，图示如下：

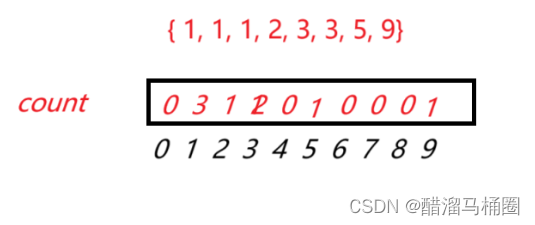
对比下来效率是非常高的，遍历一遍数组

同样，他也有局限性：

1. 不适合分散的数据，更适合集中的数据
2. 不适合浮点数、字符串、结构体数据排序，只适合整数

3.实现代码

先求最大值max和最小值min，然后遍历原数组统计次数，最后排序

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
void CountSort(int* a, int n)
{
	int min = a[0], max = a[0];
	for (int i = 1; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];
		if (a[i] > max)
			max = a[i];
	}
	int range = max - min + 1;
	int* count = (int*)calloc(range, sizeof(int));
	if (count == NULL)
	{
		printf("calloc fail!");
		return;
	}
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}
	int i = 0;
	for (int j = 0; j < range; j++)
	{
		while (count[j]--)
		{
			a[i++] = j + min;
		}
	}
}
int main()
{
	int a[] = { 10,11,10,11,15,1,2,3,5,4,2,1,0 };
	int n = sizeof(a) / sizeof(a[0]);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	CountSort(a, n);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}