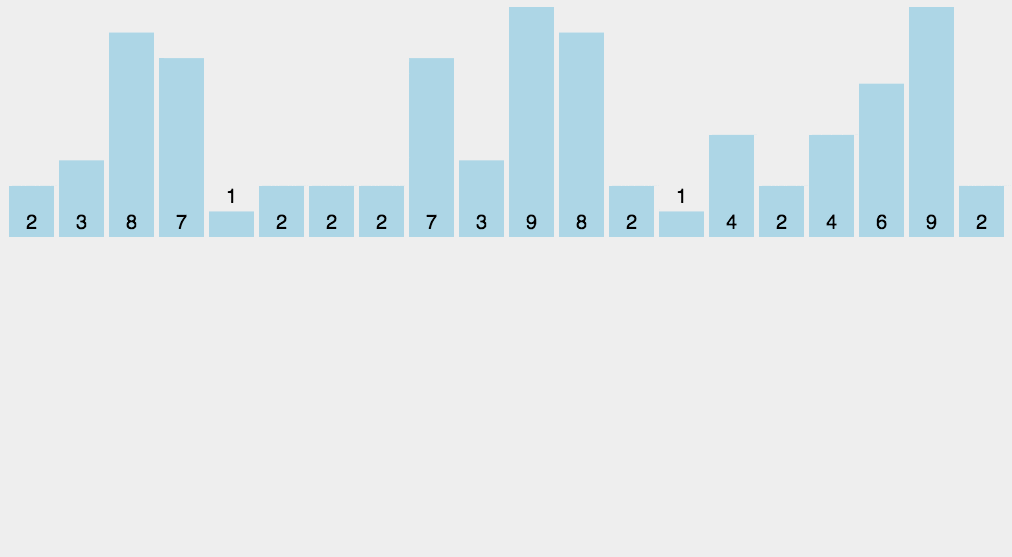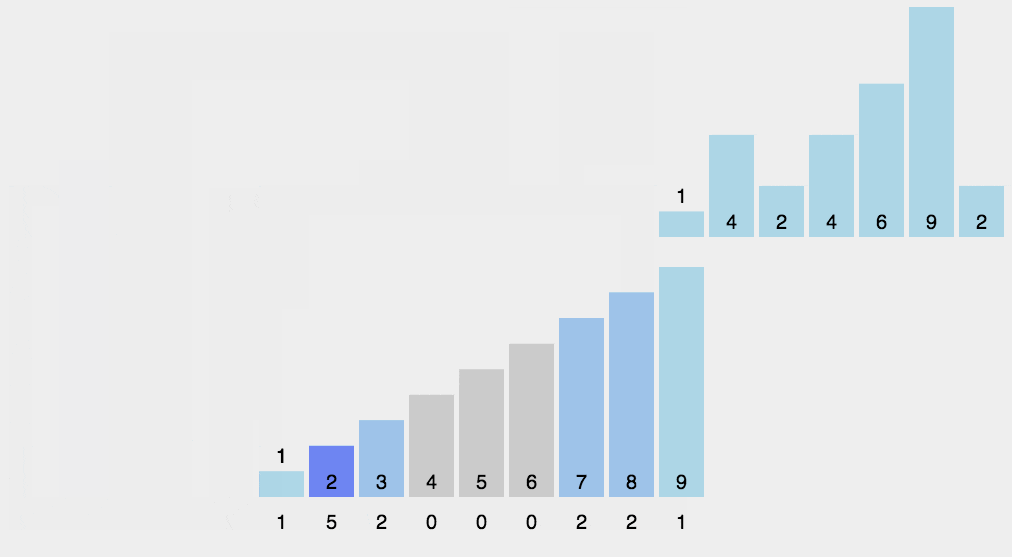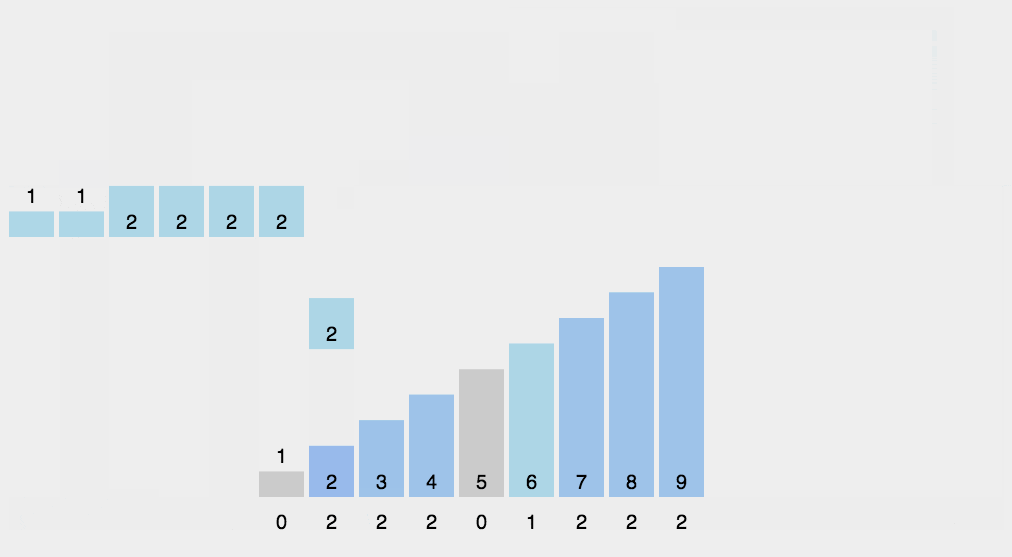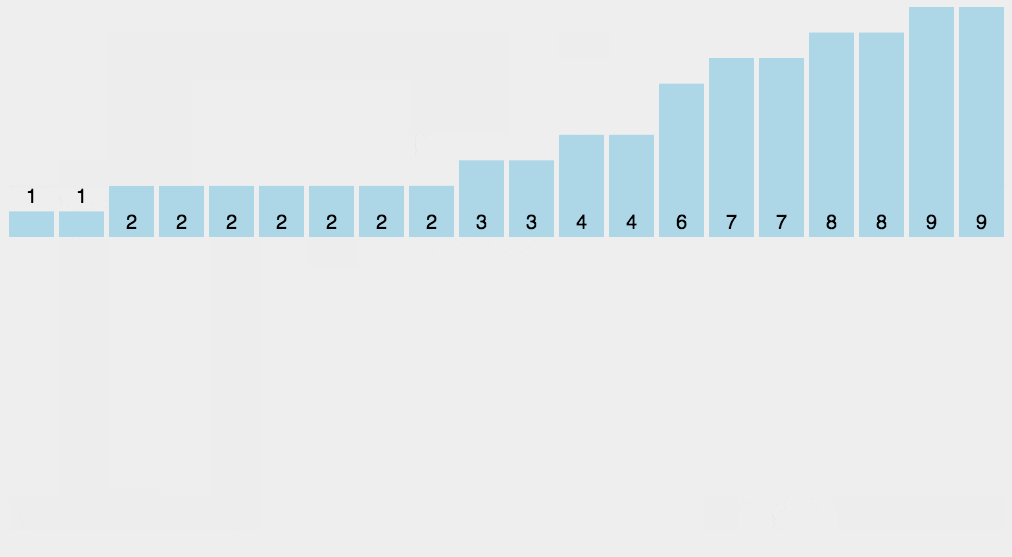课内学习的动态规划

有记忆的迭代

优化解的结构：原始问题的一部分解是子问题的解

三要素：1.子问题 2.状态的定义 3.状态转移方程 

定义

线性dp的一道例题

dp[i]表示以位置 i 结尾的方案总数，dp[4]=2，因为：首先只放一个4是可以的，4的位置之前还可以放1，我们不需要知道1之前还可以放什么数，只需要知道1的方案数加上4也是 dp[4] 的一部分方案数。

记得用前缀和来维护所有可行的方案。

二维dp

经验：列常常是1到结果、行常常是是否把这个选项 i 放入考虑范围

例题

首先：为什么用二维dp：对于选择，不能用一条线来解决，需要用一个从1到n的数组，来存储：把第一个选项纳入考虑（只是考虑，不是真放了），到把前 i 个纳入考虑（方便我们在上一个的基础上解决下一个） 

注意这里的列坐标是从 1 到 64 ，不是1到x，因为可以由一个比x更大的数异或 ai 后，结果是x，所以我们有必要保存比x大的数，（64的由来：每个进行异或的数大小不超过63，即11111111，所以进行异或和的结果也肯定不会超过11111111，即63）

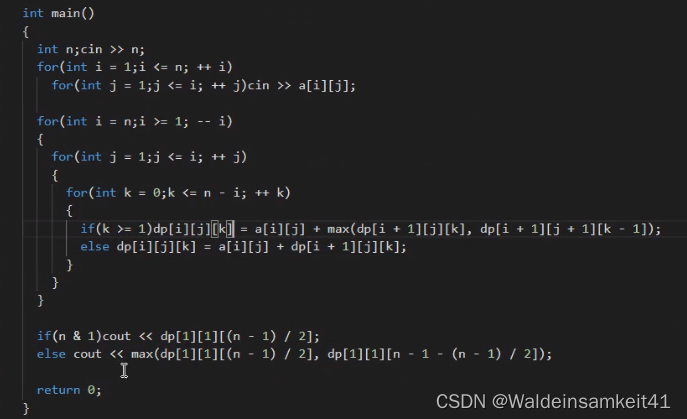
附上代码

#include <iostream>
using namespace std;

const int N = 1e5+5;
const int p = 998244353;
int dp[N][70];
int a[N];

int main()
{
  // 请在此输入您的代码
  int n,x;
  cin >> n >> x;
  for(int i = 1 ; i <= n ; i++){
    cin >> a[i];
  }
  dp[0][0]=1;
  for(int i = 1 ; i <= n ; i++){
    for(int j = 0 ; j <= 64 ; j++){
      dp[i][j] = (dp[i-1][j]+dp[i-1][j^a[i]])%p;
    }
  }
  cout << dp[n][x];

  return 0;
}

注意：什么样的数字异或 ai 后是 j ？   ---  j ^ ai 这个数字（这就要用到异或 j ^ ai ^ ai = j）

三维dp例题

多一个条件就多了一个维度，来记录k次位移。

附上代码