目录
问题
示例
方案一:
思路:
算法设计
代码实现
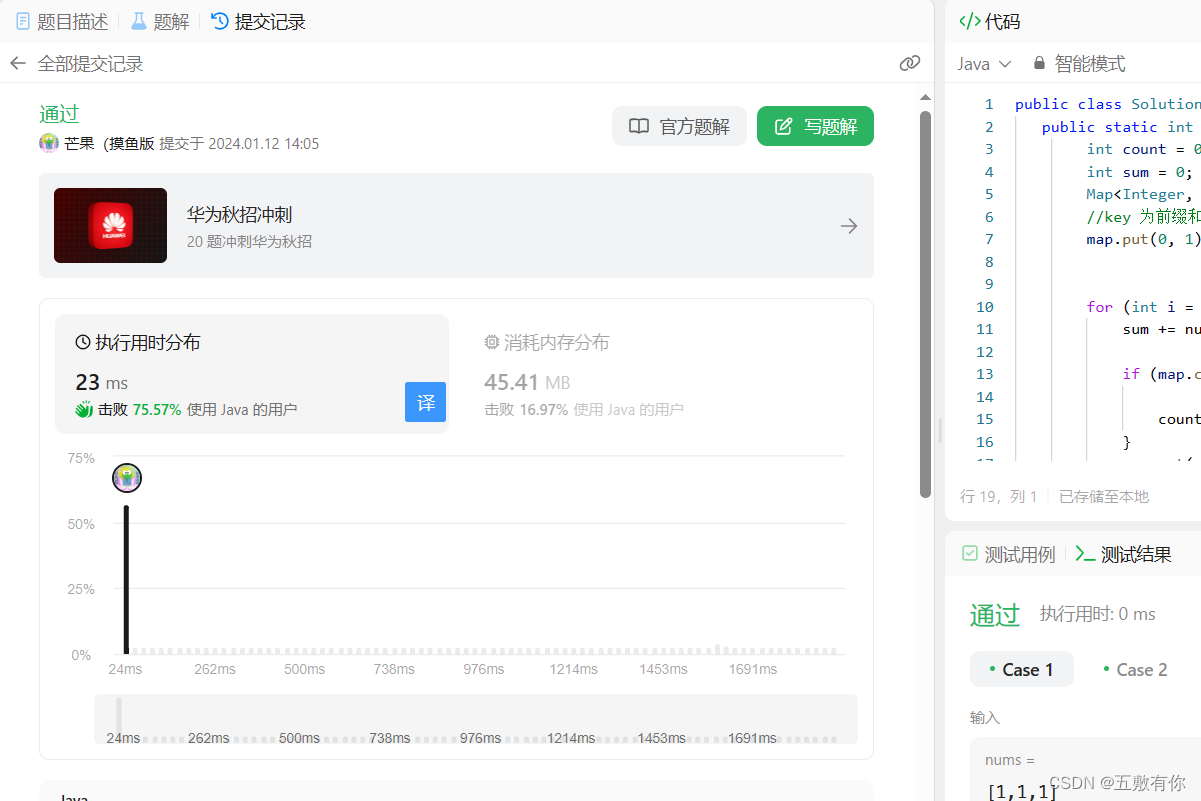
运行结果:
方案二(调优)
思路(前缀和)
算法设计
示意图
代码实现
运行结果
问题
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例
示例 1:
输入:nums = [1,1,1], k = 2 输出:2
示例 2:
输入:nums = [1,2,3], k = 3 输出:2
方案一:
思路(暴力破解)
暴力破解
算法设计
-
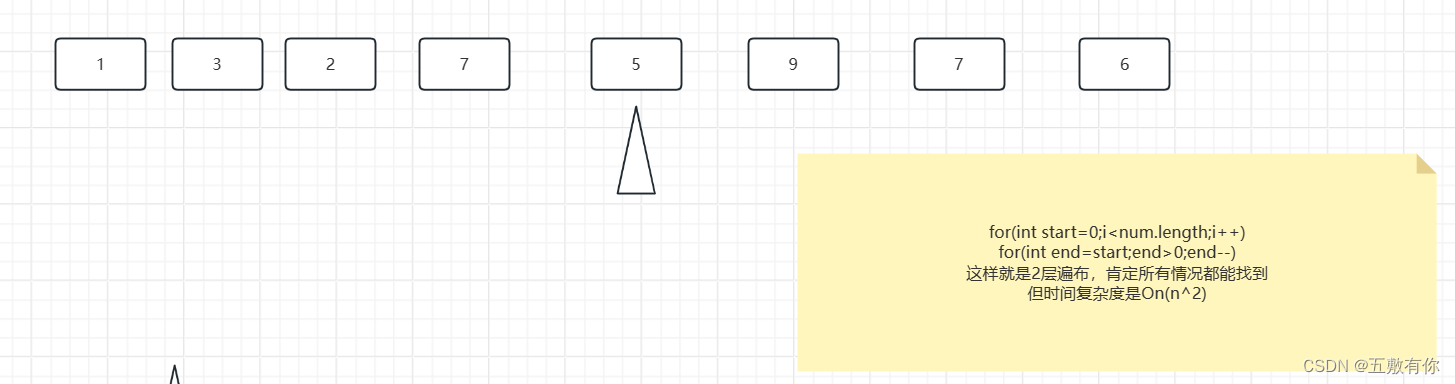
外层循环: 外层循环通过
start遍历数组的每个元素,作为子数组的起始位置。 -
内层循环: 内层循环通过
end遍历从start到数组开头的元素,计算子数组的和sum。 -
和的判断: 在内层循环中,判断当前子数组的和
sum是否等于目标值k,若相等则增加计数count。 -
返回结果: 最终返回计数
count,表示和为k的子数组的个数。
这个算法的问题在于它对每个可能的子数组都进行了遍历和计算,导致时间复杂度较高,特别是当数组规模较大时。如果数组长度为 n,则算法的时间复杂度为 O(n^2)。
算法示意图
代码实现
public class Solution {
public int subarraySum(int[] nums, int k) {
int count = 0;
for (int start = 0; start < nums.length; ++start) {
int sum = 0;
for (int end = start; end >= 0; --end) {
sum += nums[end];
if (sum == k) {
count++;
}
}
}
return count;
}
}
运行结果:
居然没有超时,超乎我的想象

但我知道肯定不能这么做。。。寻求优化
方案二(调优)
思路(前缀和)
使用前缀和的方法可以解决这个问题,因为我们需要找到和为k的连续子数组的个数。
通过计算前缀和,我们可以将问题转化为求解两个前缀和之差等于k的情况。
用一个Map集合,然后将key值为找到的前缀和,然后都存到Map中,通过不同的前缀和相减得到某个区间的一段和。
每算一次前缀和,就判断是否在map中(count是看有多少个满足条件的前缀和)
在:返回值count+=map.get(key) 然后更新这个前缀和在map中的count +1
不在:更新前缀和在map中的count+1
最后返回count即可
算法设计
- 使用单个循环迭代数组,维护累计和 (
sum)。 - 使用哈希表 (
sumCountMap) 存储遇到的和的频率,初始化为和为0的次数为1。 - 对数组中的每个元素,检查是否存在和为
(sum - k)的前缀子数组。如果存在,将相应的次数加到结果中。 - 更新哈希表,记录当前和的出现次数。
示意图
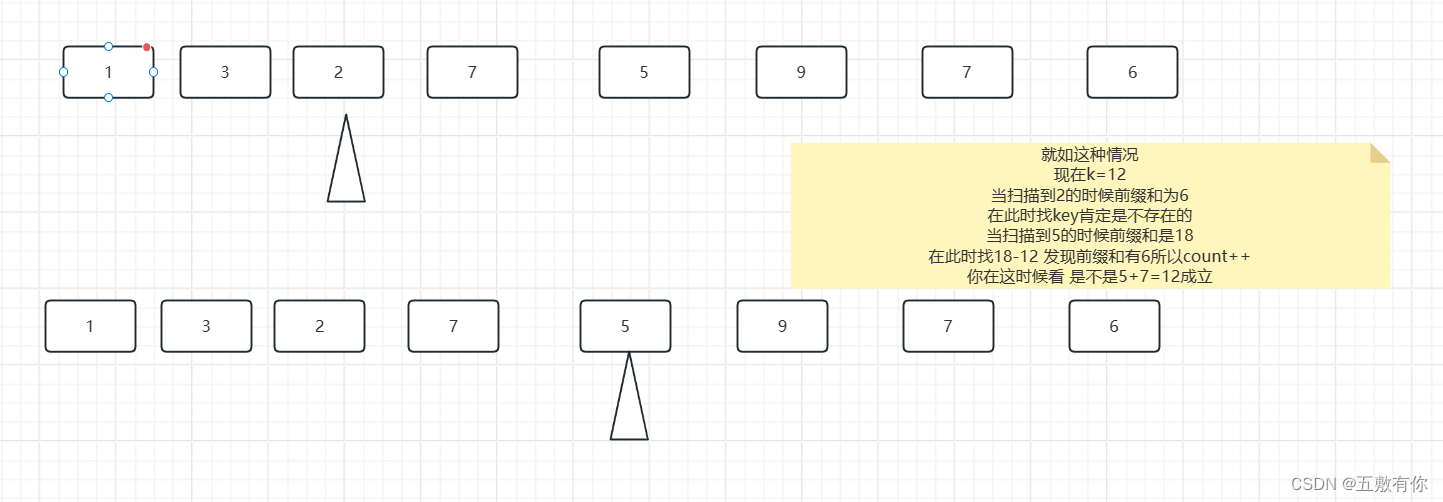
代码实现
下面是优化后的代码,使用了哈希表来记录累计和(前缀和),以便有效地确定具有和等于 k 的子数组的数量:
public class Solution {
public static int subarraySum(int[] nums, int k) {
int count = 0;
int sum = 0;
Map<Integer, Integer> map = new HashMap<>();
//key 为前缀和 value为count
map.put(0, 1); // 初始化前缀和为0的次数为1
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
//关键在这,sum-k就是在找另外一段前缀和是否存在
if (map.containsKey(sum - k)) {
count += map.get(sum - k);
}
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
return count;
}
}
运行结果
确实快噢~