文章目录
- 优先级队列(Priority Queue)
- 实现方式
- 基于数组实现
- 基于堆实现
- 方法实现
- offer(E value)
- poll()
- peek()
- isEmpty()
- isFull()
- 优先级队列的实现细节
优先级队列(Priority Queue)
优先级队列是一种特殊的队列,其中的元素不是按照进入队列的顺序出队,而是按照元素的优先级出队。在优先级队列中,元素的优先级最高的将会首先出队。
实现方式
基于数组实现
以下是基于数组的优先级队列的简单实现:
public class PriorityQueueArray<E extends Priority> {
private E[] array;
private int size = 0;
public PriorityQueueArray(int capacity) {
array = (E[]) new Object[capacity];
}
public boolean offer(E value) {
if (size >= array.length) return false;
int i = size - 1;
while (i >= 0 && array[i].priority < value.priority) {
array[i + 1] = array[i];
i--;
}
array[i + 1] = value;
size++;
return true;
}
public E poll() {
if (size == 0) return null;
E result = array[size - 1];
array[size - 1] = null;
size--;
return result;
}
public E peek() {
if (size == 0) return null;
return array[size - 1];
}
public boolean isEmpty() {
return size == 0;
}
public boolean isFull() {
return size == array.length;
}
}
这个实现中,offer方法将元素插入到正确的位置以保持数组的有序性,poll方法删除并返回优先级最高的元素,peek方法返回但不删除优先级最高的元素。isEmpty和isFull方法分别用于检查队列是否为空或已满。
基于堆实现
基于数组的实现有一些缺点。例如,插入和删除元素可能需要移动大量的元素,特别是在最坏的情况下,这可能需要移动整个数组。因此,这种实现的时间复杂度可能会达到O(n),其中n是队列的大小。
这就是为什么在实践中,我们通常会使用更复杂的数据结构,如堆,来实现优先级队列。使用堆实现的优先级队列可以在O(log n)的时间复杂度内插入和删除元素,这比基于数组的实现更有效率。
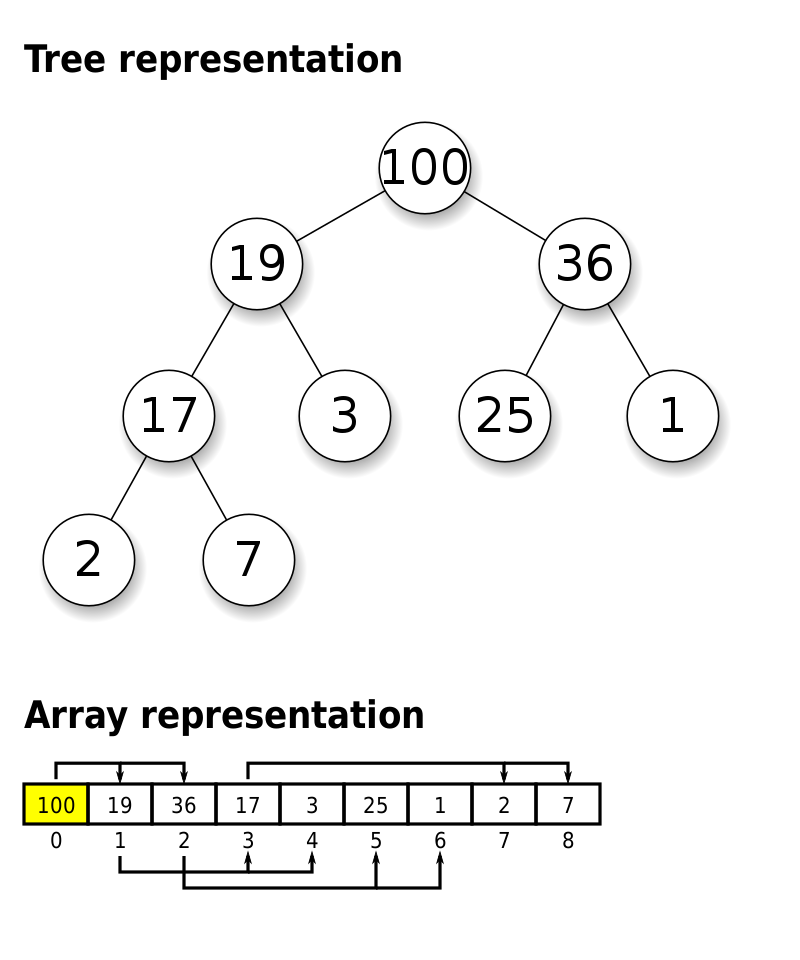
优先级队列通常使用堆(Heap)数据结构来实现。在Java中,可以通过实现Queue接口来创建一个优先级队列。下面的代码是一个使用最大堆实现的优先级队列:
public class PriorityQueue2<E extends Priority> implements Queue<E> {
Priority[] array;
public int size;
public PriorityQueue2(int capacity) {
array = new Priority[capacity];
}
...
}
这个优先级队列中的元素必须实现Priority接口,这个接口定义了元素的优先级。
方法实现
优先级队列通常包含以下方法:
offer(E value)
将元素插入到优先级队列中。如果队列已满,返回false;否则,将元素插入到正确的位置以保持堆的性质,并返回true。
@Override
public boolean offer(E value) {
if(isFull())
return false;
if (size == 0){
array[0] = value;
}
else{
int child = size;
int partent = (child - 1) / 2;
while (child > 0 && value.priority > array[partent].priority){
array[child] = array[partent];
child = partent;
partent = (child - 1) / 2;
}
array[child] = value;
}
size++;
return true;
};
poll()
移除并返回优先级最高的元素。如果队列为空,返回null。
@Override
public E poll() {
if (isEmpty())
return null;
E result = (E)array[0];
array[0] = array[size-1];
array[size] = null;
size--;
down(0);
return result;
}
private void down(int parent){
int child1 = parent * 2 + 1;
int child2 = parent * 2 + 2;
if(child1 >= size )
return;
int maxIndex = child2 < size && array[child2].priority > array[child1].priority
? child2: child1;
if(array[maxIndex].priority <= array[parent].priority)
return;
change(parent,maxIndex);
down(maxIndex);
}
private void change(int parent,int child){
Priority p = array[parent];
array[parent] = array[child];
array[child] = p;
}
peek()
返回优先级最高的元素,但不移除它。如果队列为空,返回null。
@Override
public E peek() {
if (isEmpty())
return null;
return (E)array[0];
}
isEmpty()
判断队列是否为空。
@Override
public boolean isEmpty() {
return size == 0;
}
isFull()
判断队列是否已满。
@Override
public boolean isFull() {
return size == array.length;
}
优先级队列的实现细节
优先级队列的实现主要基于一个堆结构。堆是一种特殊的完全二叉树,其中每个节点的值都大于或等于其子节点的值(最大堆)或小于或等于其子节点的值(最小堆)。
在我们的实现中,我们使用了一个数组array来存储堆的元素,并使用size来记录堆的大小。这是因为完全二叉树可以非常方便地用数组来表示。具体来说,对于数组中的任何一个元素,其左子节点的索引是2 * index + 1,右子节点的索引是2 * index + 2,而其父节点的索引是(index - 1) / 2。