先写BST树的定义及特点，然后记录BST数的删除操作。

1 BST定义及特点

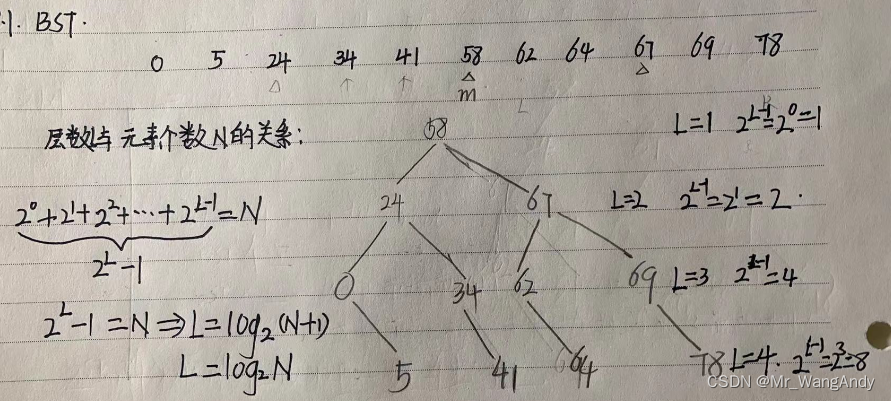
BST数是一棵特殊的二叉树，如何能得到一颗二叉搜索树呢？下面一个有序序列，经过二分搜索，得到的就是一颗BST树。根节点就是当前一轮要搜索的中间节点。
BST树称作二叉搜索树（Binary Search Tree）或者二叉排序树（Binary Sort Tree），它或者是一颗空树；或者是具有下列性质的二叉树：
1 、若左子树不为空，则左子树上所有节点的值均小于它的根节点的值
2 、若右子树不为空，则右子树上所有节点的值均大于它的根节点的值
3 、左右子树也分别满足二叉搜索树性质
特点 ：每一个节点都满足 左孩子的值（不为空） < 父节点的值 < 右孩子的值（不为空）；比如上图中，24 < 58 < 67
二叉树层数和节点的个数的关系；
二分搜索就是从根搜到叶子节点，因此，BST的时间复杂度是O(logN)

2 BST数删除操作

删除节点时，有两个概念需要分清楚：
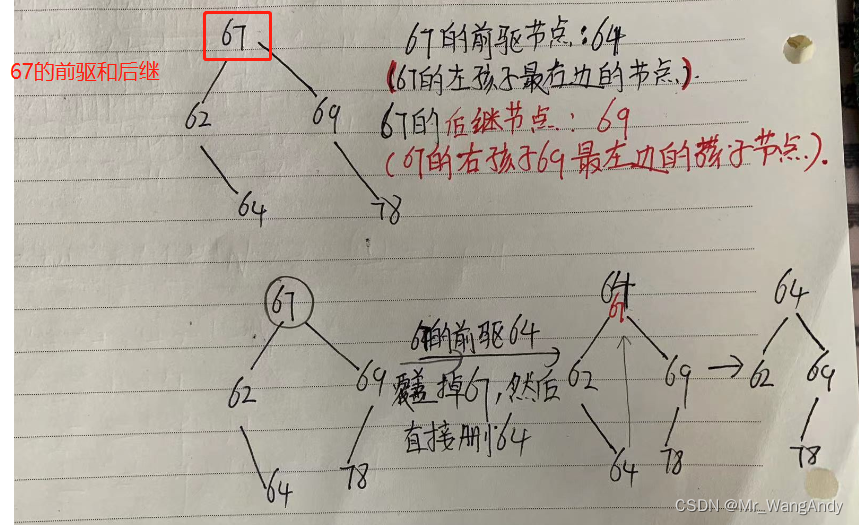
前驱节点：当前节点左子树中值最大的节点。
后继节点：当前节点右子树中值最小的节点，就是右子树中最左边的值。
假设要删除的节点就是当前遍历到的节点。
1 如果当前节点没有孩子节点，父节点地址域置为nullptr;
2 如果当前节点只有一个孩子节点，让父节点指向当前节点。

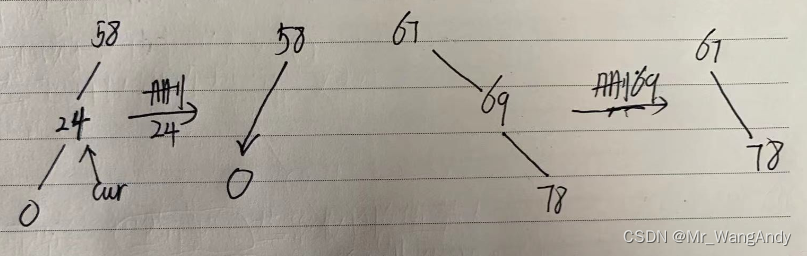
3 如果当前节点有两个孩子节点，找到当前节点的前驱节点，用前驱节点覆盖当前节点的值，然后直接删除前驱或者后继节点的值。

代码实现时候，先实现情况3。

	/* 功能：删除二叉树中的val节点
	*
	* 参数：
	*		const T & val： 待删除的节点
	*/
	void n_remove(const T & val)
	{
		if (root_ == nullptr)
		{
			return;
		}
		
		// 搜索待删除的节点，cur指向当前搜索的节点，parent指向cur的父节点
		Node *parent = nullptr;
		Node *cur = root_;
		while (cur != nullptr)
		{
			if (cur->data_ == val)   // 如果当前是根节点，说明找到了，先break出来，在情况1和2时处理。
			{
				break;  
			}
			else if (comp_(cur->data_, val))  // 用函数对象比较，如果当前节点值小于val,就从当前节点的右边找
			{
				parent = cur;
				cur = cur->right_;
			}
			else      // 否则就从左边找
			{
				parent = cur;
				cur = cur->left_;
			}
		}

		// 如果找不到要删除的节点，返回 
		if (cur == nullptr)
		{
			return;
		}

		// 走到这里说明已经找到了当前要删除的节点：比如上图中67的情况
		// 开始判断，先判断如果当前待删除节点有两个孩子，找孩子的前驱节点
		if (cur->left_ != nullptr && cur->right_ != nullptr)
		{
			parent = cur;
			Node *pre = cur->left_;
			while (pre->right_ != nullptr)   // 找前驱节点
			{
				parent = pre;
				pre = pre->right_;
			}
			cur->data_ = pre->data_;
			cur = pre;					// cur指向当前要删除的节点，parent指向其父节点。
		}

		// 找出parent最后指向的左孩子还是右孩子
		Node *child = cre->left_;
		if (child == nullptr)
		{
			child = cur->right_;
		}
		
		// 表示删除的是根节点：根节点的parent是空间点
		if (parent == nullptr)
		{
			root_ = child;
		}
		else 
		{
			// 把待删除节点 写入父节点中
			if (parent->left_ == cur)
			{
				parent->left_ = child;
			}
			else
			{
				parent->right_ = child;
			}
		}
		delete cur;  // 删除当前节点
	}