手撕乘积(Multiplication & Product): 穷举和图示(1)
乘积
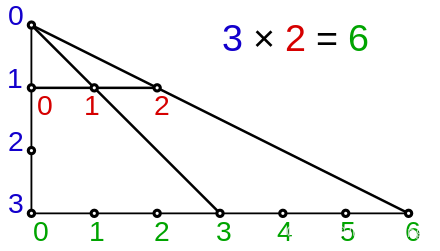

r ⋅ s = ∑ i = 1 s r = r + r + ⋯ + r ⏟ s times = ∑ j = 1 r s = s + s + ⋯ + s ⏟ r times r\cdot s=\sum _{i=1}^{s}r=\underbrace {r+r+\cdots +r} _{s{\text{ times}}}=\sum _{j=1}^{r}s=\underbrace {s+s+\cdots +s} _{r{\text{ times}}} r⋅s=i=1∑sr=s times r+r+⋯+r=j=1∑rs=r times s+s+⋯+s
4 * 3
>>> 12
.1 * .2
>>> 0.020000000000000004 # 😓
[1, 2, 3] * 2
>>> [1, 2, 3, 1, 2, 3]
[1, 2, 3] * [1, 2, 3]
>>> TypeError: can't multiply sequence by non-int of type 'list' # 😓
(1, 2, 3) * 4
>>> (1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3)
(1, 2, 3) * (1, 2, 3)
>>> TypeError: can't multiply sequence by non-int of type 'tuple'
np.array([1,2,3]) * 2
>>> array([2, 4, 6])
np.array([1,2,3]) * np.array([1,2,3])
>>> array([1, 4, 9])
np.multiply(np.array([1,2,3]), np.array([1,2,3]))
>>> array([1, 4, 9])
np.array([1,2,3]) * np.array([1,2,3,4])
>>> ValueError: operands could not be broadcast together with shapes (3,) (4,)
np.multiply(np.array([1,2,3]), np.array([1,2,3,4]))
>>> ValueError: operands could not be broadcast together with shapes (3,) (4,)
np.array([[1,2,3], [1,2,3]]) * np.array([2,3,4])
>>> array([[ 2, 6, 12],
[ 2, 6, 12]])
np.multiply(np.array([[1,2,3], [1,2,3]]), np.array([2,3,4]))
>>> array([[ 2, 6, 12],
[ 2, 6, 12]])
点乘
x = 3
y = 5
xNda = np.arange(x)
>>> array([0, 1, 2])
x2Nda = xNda*2+1
>>> array([1, 3, 5])
yNda = np.arange(1, y)
>>> array([1, 2, 3, 4])
xyNda = np.meshgrid(xNda, yNda)
>>> array([[[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2]],
[[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3]]])
np.dot(x, y)
>>> 15
np.dot(xNda, x)
>>> array([0, 3, 6])
np.dot(xNda+3, xNda+7) # 👇图示之
>>> 98
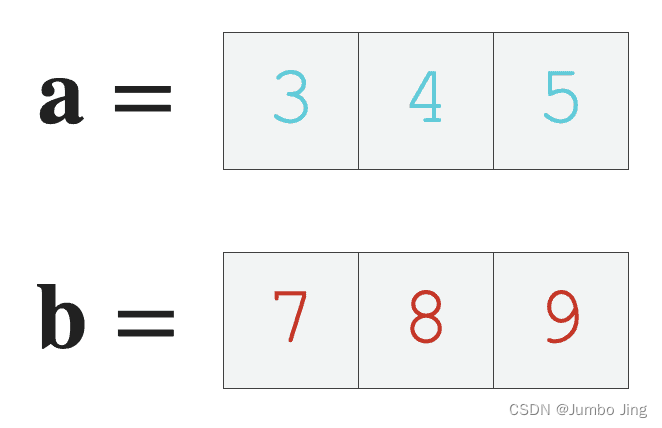
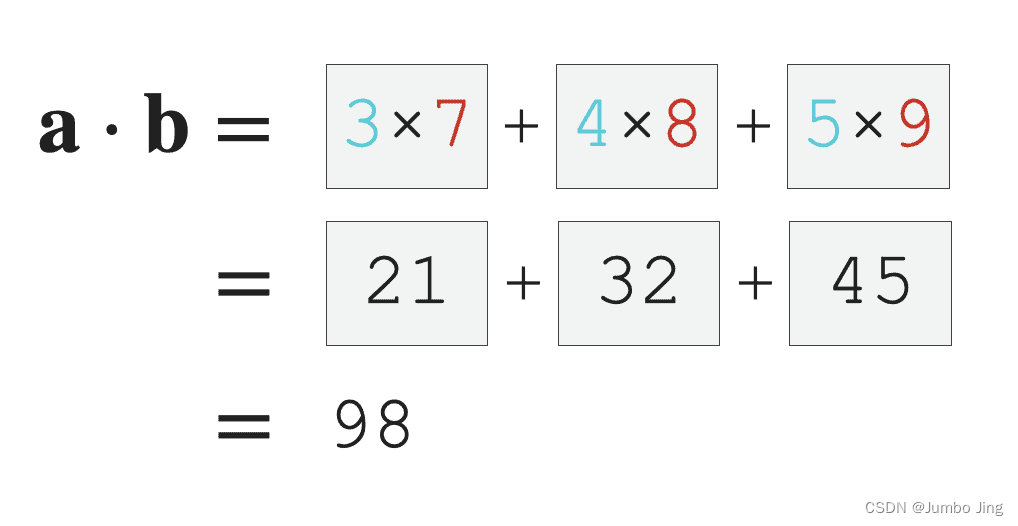
向量的点乘,也叫做向量的内积、数量积。对两个向量执行点乘运算,就是对着两个向量对应位置一一相乘之后求和的操作,点乘的结果是一个标量。
定义: 向量 a = [ a 1 , a 2 , . . . , a n ] a = [a_1, a_2, ..., a_n] a=[a1,a2,...,an] 和向量 b = [ b 1 , b 2 , . . . , b n ] b = [b_1, b_2, ..., b_n] b=[b1,b2,...,bn] 的内积为:
a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + . . . + a n b n a \cdot b = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 + ... + a_n b_n a⋅b=∑i=1naibi=a1b1+a2b2+...+anbn
特别地, 0 ⋅ a = a ⋅ 0 = 0 0 \cdot a = a \cdot 0 = 0 0⋅a=a⋅0=0;若 a , b a, b a,b 是非零向量,则 a a a 与 b b b 正交的充要条件是 a ⋅ b = 0 a \cdot b = 0 a⋅b=0。
点积的几何意义: 可以用来表征或计算两个向量之间的夹角,以及在 b b b 向量在 a a a 向量方向上的投影,有公式:
a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ a \cdot b = |a| |b| \cos \theta a⋅b=∣a∣∣b∣cosθ
其中, θ \theta θ 为 a a a 与 b b b 之间的夹角。

根据这个公式就可以计算向量 a a a 和向量 b b b 之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:
- a ⋅ b > 0 a \cdot b > 0 a⋅b>0,方向基本相同,夹角在 0 ° 0° 0° 到 90 ° 90° 90° 之间;
- a ⋅ b = 0 a \cdot b = 0 a⋅b=0,正交,相互垂直;
- a ⋅ b < 0 a \cdot b < 0 a⋅b<0,方向基本相反,夹角在 90 ° 90° 90° 到 180 ° 180° 180° 之间。
向量点乘的运算特性:
- a 2 ≥ 0 a^2 \geq 0 a2≥0;当 a 2 = 0 a^2 = 0 a2=0 时,必有 a = 0 a = 0 a=0; (正定性)
- a ⋅ b = b ⋅ a a \cdot b = b \cdot a a⋅b=b⋅a;(对称性)
- ( λ a + μ b ) ⋅ c = λ a ⋅ c + μ b ⋅ c (\lambda a + \mu b) \cdot c = \lambda a \cdot c + \mu b \cdot c (λa+μb)⋅c=λa⋅c+μb⋅c,对任意实数 λ , μ \lambda, \mu λ,μ 成立; (线性)
- cos ∠ ( a , b ) = a ⋅ b / ( ∣ a ∣ ∣ b ∣ ) \cos \angle (a, b) = a \cdot b / (|a| |b|) cos∠(a,b)=a⋅b/(∣a∣∣b∣);(余弦定理)
- ∣ a ⋅ b ∣ ≤ ∣ a ∣ ∣ b ∣ |a \cdot b| \leq |a| |b| ∣a⋅b∣≤∣a∣∣b∣,等号只在 a a a 与 b b b 共线时成立。
😓😓😓…请等下集分解
以上内容来自维基百科, 由![]() 协助完成.
协助完成.