C#中对浮点数NaN，PositiveInfinity，NegativeInfinity的特殊处理

news2025/2/27 18:14:07

NAN

NAN 整体意思为Not a Number 不是一个数，

NaN（Not a Number，非数）是计算机科学中数值数据类型的一类值，表示未定义或不可表示的值。常在浮点数运算中使用。首次引入NaN的是1985年的IEEE 754浮点数标准。

EEE 754-1985中，用指数部分全为1、小数部分非零表示NaN。以32位IEEE单精度浮点数的NaN为例，按位表示即：S111 1111 1AXX XXXX XXXX XXXX XXXX XXXX，S为符号位，符号位S的取值无关紧要；A是小数部分的最高位（ the most significant bit of the significand），其取值表示了NaN的类型：X不能全为0，并被称为NaN的payload；

NaN本质仍然是一个特殊的浮点数，即零除以零。

public const Single NaN = 0F / 0F;

而正无穷和负无穷为：

正无穷大PositiveInfinity：正数除以零，仍然是一个特殊浮点数

负无穷大NegativeInfinity：负数除以零，仍然是一个特殊浮点数

        public const Single PositiveInfinity = 1F / 0F;
        public const Single NegativeInfinity = -1F / 0F;

任何对NaN进行加减乘除，正弦、正切，幂计算都将反馈NaN，并不会抛出异常。我们在进行浮点数运算时，一定要特别注意对除以0的处理。

对NaN，无穷大等浮点数操作不会抛出异常，而是特殊处理

比如对一个数组长度为0的数组求平均值，注意要进行特殊处理：

            try
            {
                int[] testArray = new int[0];
                Console.WriteLine(testArray.Average());
            }
            catch (Exception ex) 
            {
                Console.WriteLine($"异常类型【{ex.GetType()}】,异常信息【{ex.Message}】");
            }

返回NaN的运算

返回NaN的运算有如下三种：

至少有一个参数是NaN的运算
不定式
- 下列除法运算：0/0、∞/∞、∞/−∞、−∞/∞、−∞/−∞
- 下列乘法运算：0×∞、0×−∞
- 下列加法运算：∞ + (−∞)、(−∞) + ∞
- 下列减法运算：∞ - ∞、(−∞) - (−∞)
产生复数结果的实数运算。例如：
- 对负数进行开偶次方的运算
- 对负数进行对数运算
- 对正弦或余弦到达域以外的数进行反正弦或反余弦运算 [1]

测试程序如下：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace NaN_Demo
{
    class Program
    {
        static void Main(string[] args)
        {
            float nan = float.NaN;
            float posi = float.PositiveInfinity;
            float nega = float.NegativeInfinity;
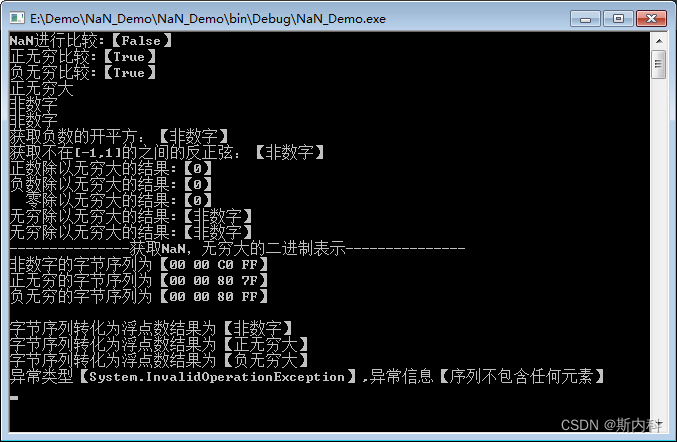
            Console.WriteLine($"NaN进行比较:【{nan == nan}】");
            Console.WriteLine($"正无穷比较:【{posi == posi}】");
            Console.WriteLine($"负无穷比较:【{nega == nega}】");
            float x = posi - nega;
            Console.WriteLine(x);
            x = posi - nan;
            Console.WriteLine(x);
            Console.WriteLine(Math.Tan(nan));
            double d = Math.Sqrt(-4);
            Console.WriteLine($"获取负数的开平方：【{d}】");
            d = Math.Asin(2);
            Console.WriteLine($"获取不在[-1,1]的之间的反正弦：【{d}】");
            Console.WriteLine($"正数除以无穷大的结果:【{1F / posi}】");
            Console.WriteLine($"负数除以无穷大的结果:【{-1F / posi}】");
            Console.WriteLine($"  零除以无穷大的结果:【{0 / posi}】");
            Console.WriteLine($"无穷除以无穷大的结果:【{posi / posi}】");
            Console.WriteLine($"无穷除以无穷大的结果:【{posi / nega}】");

            Console.WriteLine("---------------获取NaN，无穷大的二进制表示---------------");
            byte[] bufferNaN = BitConverter.GetBytes(nan);
            byte[] bufferPosiInfinity = BitConverter.GetBytes(posi);
            byte[] bufferNegaInfinity = BitConverter.GetBytes(nega);
            Console.WriteLine($"非数字的字节序列为【{string.Join("\x20", bufferNaN.Select(element => element.ToString("X2")))}】");
            Console.WriteLine($"正无穷的字节序列为【{string.Join("\x20", bufferPosiInfinity.Select(element => element.ToString("X2")))}】");
            Console.WriteLine($"负无穷的字节序列为【{string.Join("\x20", bufferNegaInfinity.Select(element => element.ToString("X2")))}】");
            Console.WriteLine();
            Console.WriteLine($"字节序列转化为浮点数结果为【{BitConverter.ToSingle(bufferNaN, 0)}】");
            Console.WriteLine($"字节序列转化为浮点数结果为【{BitConverter.ToSingle(bufferPosiInfinity, 0)}】");
            Console.WriteLine($"字节序列转化为浮点数结果为【{BitConverter.ToSingle(bufferNegaInfinity, 0)}】");
            try
            {
                int[] testArray = new int[0];
                Console.WriteLine(testArray.Average());
            }
            catch (Exception ex) 
            {
                Console.WriteLine($"异常类型【{ex.GetType()}】,异常信息【{ex.Message}】");
            }
            Console.ReadLine();
        }
    }
}