目录
一. 介绍
二. SIS问题定义
2.1 直观理解
2.2 数学定义
2.3 基本性质
三. SIS与q-ary格
四. SIS问题的推广
五. Hermite标准型
六. 小结
一. 介绍
short interger solution problem短整数解问题,简称SIS问题。
1996年,Ajtai首次提出SIS问题,由此设计出了单向函数(one-way function),抗碰撞的哈希函数(collision resistant hash function),身份验证方案(identification scheme),数字签名(digitao signatures)等等。这些在网络安全领域,可以被称之为minicrypt原语。
本文章将介绍SIS问题,探究它与最坏情况格问题的关系,研究其基本的性质以及密码学中的应用。
二. SIS问题定义
2.1 直观理解
SIS问题的抽象代数表达形式:
在一个有限但足够大的加法群(additive group)中,所有的元素都是均匀且随机可以被取到的,如何寻找一种整数倍的组合,使他们的和为0,且要求这种组合的足够短。这个问题是困难的。
如果给出一些参数,问题会变得更加距离。
给出一个正整数n和q,由此形成群:
给定一个正实数,从群中抽取m个样本。
在以上这些参数中,m有的时候会被省略不写,n是我们通常所说的安全参数(比如n>100),要求和
与n之间呈现多项式关系,且满足:
2.2 数学定义
给定m个均匀随机的n维向量,将他们作为矩阵的列,由此形成
。如何寻找一个非零的整数向量
,且范数满足
,使其满足:
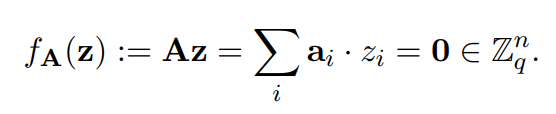
理解:
可以看成SIS函数,A为公开的下标。很明显该函数正向计算容易,逆向计算z困难。
2.3 基本性质
(1)z的长度
如果不限定向量z的长度,那么可以直接借助高斯消元法(Gaussian elimination)找出一个答案z。另外z的上限肯定满足:
如果不限定的话,则会出现很多平凡解(trivial),比如:
(2)扩展矩阵
将矩阵A可以扩展为:
原来的z增加后续的0即可,此时解z的范数是不会改变的。简单来讲就是,当m增大时,SIS问题会变得简单。当n增加时,SIS问题会变得困难。
(3)参数的取值范围
向量z的范数上限以及向量
的样本个数m都需要足够大,来保证问题至少有解。根据鸽子洞理论(pigeonhole argument),我们考虑一个临界值如下:
此时向量的空间至少大小为:
说明在中至少有两个重复的解,也就是存在不同的
x,x'满足:
将两者相减可得:
换句话说z=x-x',且其范围是:
也就是保证了SIS问题的有解性。也就是SIS问题中的参数需要满足:
(4)抗碰撞的SIS函数
将此处小整数解定义为只能取0或1,那么可形成如下函数族:
假定SIS问题是困难的,说明找不到其对应的短整数解z,也就找不到两个不同的x使其函数相等,也就是:
当然此处的小整数不仅仅只能取0和1,推广其他较小的范围也可以。
三. SIS与q-ary格
网络安全领域有一个很有意思的m维整数格,叫做q-ary垂直格。SIS问题可以看成平均情况的短向量问题,如下:
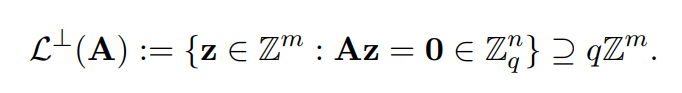
很明显是其子格。
借鉴编码理论(coding theory),此处的矩阵A可以看成q-ary垂直格的校验矩阵。SIS问题与SVP问题之间的关系:
均匀随机选择A,SIS问题的本质就是在q-ary垂直格上找到一个足够短的非零向量。
四. SIS问题的推广
SIS问题的推广也可以称之为inhomogeneous版本。也就是当均匀且随机选择矩阵A和向量u时,尝试找出如下等式足够短的整数解x:
如果不限定向量的长度,此方程所有的解可以构成陪集格(lattice coset),如下:
其中,为方程的解。
选择合适的参数,推广后的SIS问题和原来的SIS问题是等效的。
五. Hermite标准型
原始的SIS问题中的矩阵A为n行m列,我们可以把该矩阵切成两个块状矩阵,一个矩阵是n行n列,一个矩阵是n行m-n列,由此可得:
很明显A1矩阵为方阵,可以直接求逆。接着我们对A进行变换可得:
![]()
将In作为可忽略的子矩阵。因为矩阵A2是均匀随机的,与A1是互相独立的,可得也是均匀且随机的。也就是以下两个矩阵的SIS问题的解是相同的:
所以可得矩阵A和是互相等效的。
其实这个地方对矩阵的变换,类似于网络安全纠错码(error-correcting code)中对称的生成矩阵。
六. 小结
随着网络安全的快速发展,能够抵抗量子计算攻击且支持数据隐私保护和安全处理的密码算法是目前的迫切需求。基于格的密码体制被普遍认为能够抵抗量子计算攻击,所以其研究近十年来发展迅速。从格算法应用于分析非格公钥密码体制如背包密码体制、RSA 体制的安全性,发展到基于格计算困难问题的密码体制设计,再到基于格计算困难问题设计全同态加密体制。
针对格中SVP问题的求解,第一个格基约化算法是在1982年提出的 LLL算法。该算法可以在多项式时间内,输出近似短向量。LLL算法也是至今唯一可以证明是多项式时间运行的格基约化算法。LLL算法的提出对格理论的研究,特别是公钥密码算法分析起到了很大的推动作用,另外 LLL算法在计算代数和计算数论等领域也有广泛的应用,已被公认为是20世纪最重要的算法之一。
推荐阅读:
格密码LLL算法:如何解决最短向量SVP问题(1)-CSDN博客
格密码LLL算法:如何解决最短向量SVP问题(2)_lll算法复杂度-CSDN博客
格密码LLL算法:如何解决最短向量SVP问题(3)(完结篇)-CSDN博客